Complex Numbers
Overview
Complex numbers evolved because mathematicians wanted to be able to solve mathematical problems that could not be solved using real numbers alone. During the sixteenth century CE, a number of mathematicians were trying to find a way of solving various types of polynomial equation, including second degree (quadratic) equations and especially third degree (cubic) equations. They were hampered by the fact that such equations were still relatively poorly understood. Today, we know that an nth degree polynomial equation will have a total of n roots (solutions), including roots that may be complex numbers. This knowledge is embodied in the fundamental theorem of algebra. The theorem would not begin to emerge in any meaningful form, however, until the seventeenth century CE. A further problem was that many mathematicians were still reluctant to recognise the legitimacy of negative numbers, or to accept that equations could have negative roots (which of course they frequently do).
At the forefront of the search for solutions to various forms of the cubic polynomial equation were the Italian mathematician and engineer Niccolò Fontana Tartaglia (1499-1557) and the Italian mathematician Gerolamo Cardano (1501-1576). Tartaglia came up with a general solution that worked for all forms of the cubic equation, which he (somewhat reluctantly) passed on to Cardano, on the condition that Cardano did not reveal the solution to anyone until Tartaglia had had an opportunity to publish his findings. Although he subsequently went back on his word, and published the solution in his book on algebra Ars Magna in 1545, he did at least have the decency to acknowledge Tartaglia's contribution. Meanwhile, Cardano discovered something rather strange when he attempted to solve the following cubic equation:
x3 = 15x + 4
The expression he arrived at, when he applied Tartaglia's solution to this equation, included as one of its terms the square root of minus one hundred and twenty one (√-121). This perplexed Cardano, because he knew that the square root of a negative number could not be expressed as a real number. And yet he also knew that it must ultimately lead to a real solution, namely x = 4. Tartaglia himself was unable to shed any light on the matter. Cardano subsequently published the solution to similar problems in his Ars Magna in which he somehow contrived to manipulate such terms, but by his own admission, he did not fully understand his own calculations. For this reason, Cardano is often credited with having been the first mathematician to use complex numbers, but it is more the case that he was the first to demonstrate that such things might exist. He was however the first mathematician to come up with solutions to polynomial equations that were negative numbers (which he called fictitious numbers).
The next chapter in the story of complex numbers concerns the Italian mathematician Rafael Bombelli (1526-1572). Bombelli re-examined a formula published by Cardano for solving cubic equations of the form x3 = cx + d, which (using modern notation) looks like this:
x = 3√( d/2 + √e ) + 3√( d/2 - √e )
The variable e here represents the expression ( d/2 )2 - ( c/3 )3. Bombelli applied Cardano's formula to the solution of the equation x3 = 15x + 4 (the same equation that had previously caused Cardano such consternation) and got essentially the same result as Cardano:
x = 3√( 2 + √-121 ) + 3√( 2 - √-121 )
He therefore had to deal with same problem as Cardano - namely the presence of a term that was the square root of a negative number. Undaunted, Bombelli continued to manipulate the equation in the hope of finding a solution that made sense. Although we won't reproduce the various stages that Bombelli went through here, he was eventually able to determine that:
3√( 2 + √-121 ) = 2 + √-1
and
3√( 2 - √-121 ) = 2 - √-1
You may not immediately be able to see how Bombelli arrived at these results, but we can verify that they are correct. In fact, if you have a calculator that can handle complex numbers you can verify it for yourself. Failing that, try entering each of the following expressions into Google:
[1] (2 + (-121) ^ (1/2)) ^ (1/3)
[2] (2 - (-121) ^ (1/2)) ^ (1/3)
These expressions are the ASCII equivalent of 3√( 2 + √-121 ) and 3√( 2 - √-121 ) respectively. They have to be entered in this format because Google's built in calculator can only accept ASCII characters as input, although it obviously understands the significance of i in this context! The output will be 2 + 1i for the first expression and 2 - 1i for the second (the one in front of i in both cases is totally superfluous, and you can ignore it). Substituting the simplified terms into his original equation, Bombelli now had the following:
x = 2 + √-1 + 2 - √-1 = 4
What we are looking at here is essentially the addition of two complex numbers (2 + i and 2 - i). The result of Bombelli's machinations is a solution (x = 4) that could probably be determined simply by looking at the original equation. Nevertheless, Bombelli's efforts brought to the fore the rather inconvenient fact that the solution of polynomial equations would inevitably involve the square roots of negative numbers. This meant that mathematicians would have to find a way of dealing with them. In his book L'algebra, written in 1572, Bombelli outlined the concept of a complex number system, and laid down a set of rules for arithmetic operations (addition, subtraction, multiplication and division) involving complex numbers. We probably should point out here that the polynomial equation x3 - 15x - 4 = 0 actually has three real roots, as can be seen by examining the graph of the corresponding function shown below, although only one of these roots (x = 4) is positive.
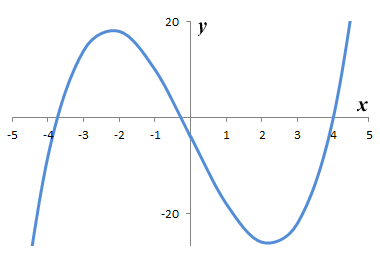
The graph of y = ƒ(x) = x3 - 15x - 4
By the end of the eighteenth century, complex numbers were being routinely used in the solution of polynomial equations, but there was still resistance in some quarters to the idea that they could be considered numbers in their own right, or that they existed within a number system distinct from the real number system. Nevertheless, the concept of a complex number system was beginning to gather support. In 1799, the German mathematician and physicist Johann Carl Friedrich Gauss published a paper containing a proof that an nth degree polynomial equation has n roots of the form a + bi, in which a and b are real numbers, and i represents the imaginary unit (√-1) - in other words, that the roots of any polynomial can be expressed as complex numbers.
Complex numbers also began to find applications in other areas, notably in the simplification of calculations involving trigonometric functions. In 1806, the Swiss amateur mathematician Jean-Robert Argand (1768-1822) not only presented a rigorous proof of the fundamental theorem of algebra, but also published an essay that described how complex numbers could be represented as points on a two-dimensional plane, in much the same way that points are represented using Cartesian coordinates on a two-dimensional geometric plane. The idea of representing complex numbers as points on a "complex plane" (as it became known) had first been put forward by the Norwegian-Danish mathematician and cartographer Casper Wessel (1745-1818). Gauss also leant his weight to the idea. He published an exposition on complex numbers as points in the complex plane in 1831, in which he also established much of the notation and terminology used today. Complex numbers now find applications in mathematics, the physical sciences, telecommunications, and just about all branches of engineering.
Properties of complex numbers
A complex number is made up of two parts - a real part, and an imaginary part (hence the name complex number). The set of complex numbers is usually signified using the symbol ℂ (a double-struck C). If you are not familiar with the concept of imaginary numbers, it might be a good idea to read the page entitled "Imaginary Numbers" before reading this page. A complex number takes the form:
a + bi
where a and b are real numbers, and i is the imaginary unit (√-1). Although a and b are both real numbers, a is called the "real" part of the complex number, while b is considered to be the "imaginary" part, since it is multiplied by the imaginary unit i. It shouldn't really be too hard to accept that a number can be constructed from two distinct and separate numeric components - after all, we all accept and are familiar with fractions, and every fraction consists of a numerator part and a denominator part.
A complex number a + bi for which the imaginary part is zero (i.e. b = 0) is effectively the real number a. This means that every real number can be expressed as a complex number. Furthermore, for any real number n, there must be infinitely many complex numbers that have n as their real part, because the imaginary part of a complex number is also a real number. This means that, like the set of all real numbers, the set of complex numbers is uncountably infinite. A complex number a + bi for which the real part is zero (i.e. a = 0) is effectively the imaginary number bi. We call such a number a purely imaginary number.
Mathematicians tend to refer to the real numbers as a field rather than a set, because the word set implies something that can be counted. For the same reason, they also refer to the set of complex numbers as a field. Whereas the real numbers exist within an ordered field, however, the complex numbers do not. For any two real numbers, one must always be greater than or less than the other. As you will see when we look at the complex plane, however, two different complex numbers can be of equal magnitude. The complex numbers are therefore considered to exist within an unordered field (note, however, that two complex numbers can be considered to be the same complex number only if their real parts and their imaginary parts are identical).
The complex plane
Because a complex number consists of two distinct parts, we can visualise it as a point in a two-dimensional Cartesian coordinate system. We call this coordinate system the complex plane. We identify each point on the complex plane using x and y coordinates, in the same way that we identify points on a two dimensional geometric plane. In fact, using the complex plane we find a number of parallels between the study of complex numbers and the study of geometry. These similarities will become self-evident as we progress. By convention, the horizontal x-axis of the complex plane is used to represent the real part of a complex number, and the vertical y-axis is used to represent the imaginary part. The x and y axes are sometimes labelled Re and Im respectively, to show that they represent the real and imaginary axes. We will be using that convention here. The complex number 5 + 4i is represented on the complex plane as follows:
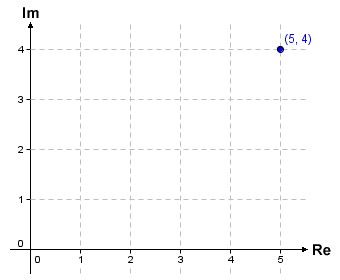
The complex number 5 + 4i plotted as a point on the complex plane
This kind of visual representation of complex numbers is sometimes called an Argand diagram, after Jean-Robert Argand, who we mentioned earlier. Note that we have identified the complex number on the diagram using a pair of comma-separated values inside brackets. The first value represents the real part of the complex number, while the second value represents the imaginary part. A complex number displayed in this format is said to be in its Cartesian, rectangular or algebraic form. The real and imaginary coordinate pair describes not only the complex number's position on the complex plane, but also its displacement from the origin (if you have studied vectors in any depth, you will no doubt be familiar with the concept of position vectors and displacement vectors). In the complex plane, the distance between a complex number and the origin is known as its modulus, and can be represented by a line connecting the origin to the point that represents the complex number.
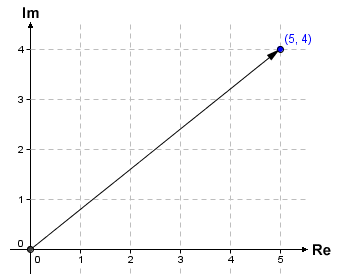
The arrow represents the modulus of the complex number 5 + 4i
The modulus of a complex number represents its magnitude (absolute value). All points on the complex plane that are the same distance from the origin have the same modulus, and hence the same absolute value. Looking at the diagram, you should be able to see that the modulus of a complex number (i.e. the distance between it and the origin) will be equal in length to the hypotenuse of a right-angled triangle in which the length of the horizontal and vertical legs correspond to the value of the real and imaginary parts of the complex number respectively. We can therefore find the absolute value of a complex number using Pythagoras' theorem. Let's suppose we want to find the absolute value of a complex number, z. The required formula is:
|z| = √( x 2 + y 2 )
where x and y represent the real and imaginary coordinates of the complex number z in the complex plane (note that vertical bars surrounding a variable are used to denote its absolute value). Let's apply this formula to the complex number 5 + 4i to find its modulus, r:
r = |5 + 4i| = √(52 + 42) = √(41) = 6.403
Although many points in the complex plane (an infinite number, in fact) can have the same modulus, each point in the complex plane is uniquely identified using a combination of its modulus and the angle between the modulus and the positive real axis, measured anti-clockwise from that axis. This angle, usually denoted using the lower-case Greek letter phi (φ), is called the argument of the complex number. For a complex number z, we would express the argument of that complex number as arg(z). The modulus and the argument of a complex number together are known as its polar coordinates. There are two possible ways, then, to specify the position of a complex number in the complex plane. We can use either its Cartesian coordinates or its polar coordinates.
We have already seen how we can use Pythagoras' theorem to find the modulus of a complex number using its x and y coordinate values. Using these same coordinates, we can use trigonometry to find its argument. The precise formula used for finding the argument φ of a complex number will depend on the sign of both the x and y coordinates. Let's deal with some trivial cases first. If a complex number z has an absolute value of zero (i.e. z = 0 + 0i), then obviously the x and y coordinates will also both be zero, and the value of φ is said to be undefined.
If only the imaginary part of the number is zero, y will also be zero, and the value of φ will depend on whether x is positive or negative. For positive values of x, φ will have a value of zero degrees (0°). For negative values of x, φ will have a value of one hundred and eighty degrees (180°). Conversely, if only the real part of the number is zero, x will also be zero, and the value of φ will depend on whether y is positive or negative. For positive values of y, φ will have a value of ninety degrees (90°). For negative values of x, φ will have a value of two hundred and seventy degrees (270°).
This leaves four possible cases for a complex number z = x + yi. In the first case we look at, z has both a positive real part and a positive imaginary part. It will be represented by a point within the first quadrant (the upper-right quadrant) of the complex plane. We can therefore obtain the argument φ of z as follows:
φ = arg (z) = arctan ( y/x )
We have already obtained the modulus r (see above) for the complex number 5 + 4i. Let's now find the argument φ for this complex number:
φ = arg (5 + 4i) = arctan ( 4/5 ) = 38.66°
Below, we can see the complex number 5 + 4i represented as a point in the complex plane, labelled with its Cartesian coordinates. The modulus and argument of the complex number (i.e. the polar coordinates) are also shown on the diagram.
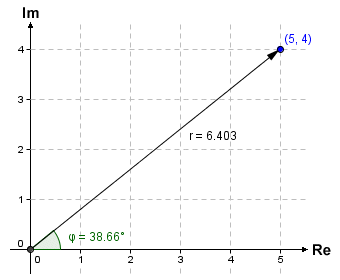
The complex number 5 + 4i in the complex plane.
If z has a negative real part and a positive imaginary part, it will be represented by a point that lies within the second quadrant (the upper-left quadrant) of the complex plane. In this case, we can obtain the argument φ of z using:
φ = arg (z) = 180 + arctan ( y/x )
Let's find the polar coordinates for the complex number -6 + 3i, whose point representation falls within the second quadrant of the complex plane. The calculation to find the modulus r will be the same as before:
r = |-6 + 3i| = √(-62 + 32) = √(45) = 6.708
Here is the calculation for the argument φ of -6 + 3i:
φ = arg (-6 + 3i) = 180 + arctan ( 3/-6 ) = 180 - 26.57 = 153.43°
Here is the complex number -6 + 3i represented as a point in the complex plane, together with its Cartesian and polar coordinates:
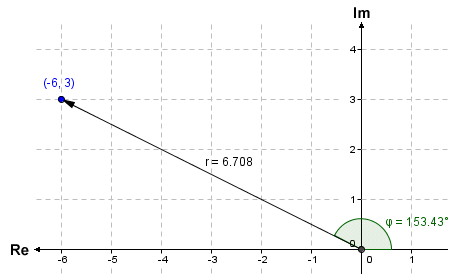
The complex number -6 + 3i in the complex plane
A complex number z that is represented by a point in the third quadrant (the lower-left quadrant) of the complex plane has both a negative real part and a negative imaginary part. Here, we obtain the argument φ of z using:
φ = arg (z) = -180 + arctan ( y/x )
This time, we will find the polar coordinates for the complex number -4 - 2i, whose point representation falls within the third quadrant of the complex plane. The calculation to find the modulus r will be:
r = |-4 - 2i| = √((-4)2 + (-2)2 ) = √(20) = 4.472
Here is the calculation for the argument φ of -4 - 2i:
φ = arg (-4 - 2i) = -180 + arctan ( -2/-4 ) = -180 + 26.57 = -153.43°
Note that negative angles are measured clockwise from the positive real axis. The result given as a positive angle (i.e. measured anti-clockwise from the positive real axis) is equivalent to this negative angle plus three hundred and sixty degrees. In order to express the argument of the complex number -4 - 2i as a positive angle, therefore, we could write the following:
φ = 360° + (-153.43°) = 206.57°
Here is the complex number -4 - 2i represented as a point in the complex plane, together with its Cartesian and polar coordinates:
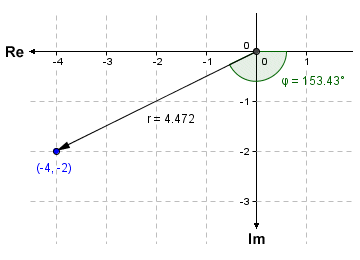
The complex number -4 - 2i in the complex plane
A point in the fourth quadrant (the lower-right quadrant) of the complex plane represents a complex number z that has a positive real part and a negative imaginary part. The argument φ of z can be found using the formula:
φ = arg (z) = arctan ( y/x )
This formula probably looks familiar to you, as it should. It is the same formula that we used to find the argument of a complex number represented by a point in the first quadrant. This time, however, the arctangent of y/x will yield a negative result. This means that the angle will again be measured clockwise from the positive real axis. Let's find the polar coordinates for the complex number 2 - 3i, whose point representation falls within the fourth quadrant of the complex plane. The calculation to find the modulus r will be:
r = |2 - 3i| = √(22 + (-3)2 ) = √(13) = 3.606
Here is the calculation for the argument φ of 2 - 3i:
φ = arg (2 - 3i) = arctan ( -3/2 ) = -56.31° (or 303.69°)
Here is the complex number 2 - 3i represented as a point in the complex plane, together with its Cartesian and polar coordinates:
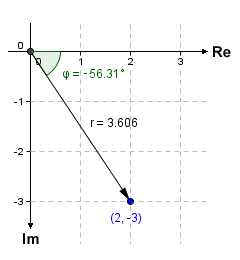
The complex number 2 - 3i in the complex plane
As you might expect, there are a number of alternative formulae for finding both the polar and the Cartesian coordinates of a complex number's point representation in the complex plane. The formula used in a given situation will depend entirely on what information is available, and of course on the result we are trying to obtain. When we start to look at arithmetic operations that can be carried out on complex numbers, we will be looking at both algebraic methods of solving problems, and methods that involve trigonometry. One very useful formula to remember allows us to derive the value of a complex number z = x + yi from its polar coordinates as follows:
z = x + yi = r(cos φ + i sin φ) = r(cos φ) + r(sin φ)i
Hopefully, you are now better able to appreciate what complex numbers are all about. Essentially, real numbers exist only on a one-dimensional number line, represented here by the real axis of the complex plane. Similarly, imaginary numbers also only exist on a one-dimensional number line, represented here by the imaginary axis of the complex plane. Although both real and imaginary numbers are useful in their own right, the complex number system brings these two number types together, enabling us to create numbers that exist on a two dimensional plane and thereby giving us a powerful tool with which to solve complex mathematical problems.
The complex conjugate
The complex conjugate of a complex number is the number with an equal real part and an imaginary part that is equal in magnitude but opposite in sign. So, for example, the complex conjugate of a + bi is a - bi. To obtain the complex conjugate (or just conjugate) of a complex number, all you need to do is change the sign of the imaginary part of the complex number. The conjugate of the complex number z = x + yi can be expressed as shown below. Note that the conjugate of the complex number is indicated by placing a bar, usually called an overbar (although the formal term is vinculum), over the name of the complex number.
z = x - yi
The fact that we are negating the imaginary part of the complex number to obtain the conjugate has two consequences. First, if the imaginary part of the complex number is zero, then the conjugate of the complex number will be the complex number itself (which will effectively be a real number). Second, the point representation of the complex conjugate in the complex plane will be a reflection of the point representation of the complex number in the real (x) axis. The illustration below shows the complex number 3 + 2i and its conjugate 3 - 2i as points in the complex plane.
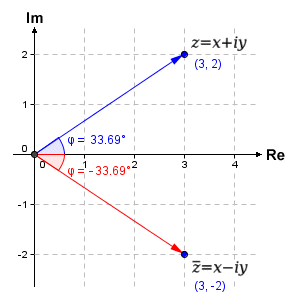
The complex conjugate negates the imaginary part of a complex number
As you can see from the diagram, the complex conjugate is found by reflecting z across the real axis. The complex conjugate can be quite useful in a number of situations, as we shall see in due course. It is routinely used, for example, to simplify the formula for dividing one complex number by another, or for finding the reciprocal of a complex number. Complex conjugates are also useful for finding the roots of polynomials. According to the complex conjugate root theorem, if a complex number is a root to a polynomial in one variable with real coefficients (e.g. the quadratic or the cubic equation), its conjugate will also be a root of that polynomial.
Addition and subtraction
Adding two complex numbers together algebraically is perfectly straightforward. All we have to do is to add the real and the imaginary parts of the summands (the complex numbers we wish to add together). Let's assume we have two complex numbers, a + bi and c + di. The formula for adding these complex numbers together is:
(a + bi) + (c + di) = (a + c) + (b + d)i
For example, let's say we wanted to add the complex numbers 4 + 9i and 2 + 8i. Applying the formula shown above, we get:
(4 + 9i) + (2 + 8i) = (4 + 2) + (9 + 8)i = 6 + 17i
Subtraction is also fairly straightforward. Let's suppose that this time we want to subtract the complex number a + bi from the complex number c + di. The formula we would use to find the difference of these two complex numbers is:
(c + di) - (a + bi) = (c - a) + (d - b)i
For example, let's say that we want to subtract the complex number 4 + 9i from the complex number 5 + 3i. Applying the formula for subtraction as shown, we get:
(5 + 3i) - (4 + 9i) = (5 - 4) + (3 - 9)i = 1 - 6i
We can also carry out addition and subtraction graphically using the complex plane. This process is essentially vector addition, because we are adding the displacement vectors of the two complex numbers. One common way of achieving this is to construct a parallelogram in which the displacement vectors form two adjacent sides of a parallelogram. The origin of the complex plane is one vertex of the parallelogram. The result of adding the complex numbers is a complex number whose point is represented on the complex plane by the vertex of the parallelogram that lies opposite the origin. The diagram below shows how we can use such a construction to find the result of adding together the complex numbers 3 + i and 2 + 3i. The result is a point with Cartesian coordinates (5, 4), which represents the complex number 5 + 4i.
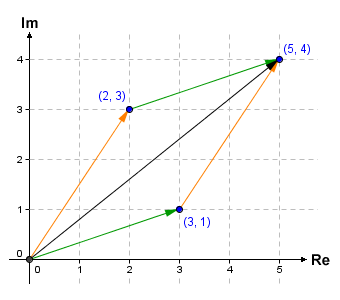
Complex number addition in the complex plane using displacement vectors
Subtraction can be carried out using the same method. Although we are talking about subtraction, we can still think of this as addition. We have two complex numbers, one of which (the subtrahend) must be subtracted from the other (the minuend). If we negate the subtrahend, we can then simply add it to the minuend. To negate a complex number, we simply reverse the sign of both the real part and the imaginary part. Let's suppose we want to take the complex number 2 + 3i (the subtrahend) away from the complex number 6 + 2i (the minuend). We start by negating 2 + 3i to get the complex number -2 - 3i. Now we simply construct our parallelogram as before. The diagram below shows the result of adding together the complex numbers 6 + 2i and -2 - 3i. The result is a point with Cartesian coordinates (4, -1), which represents the complex number 4 - i.
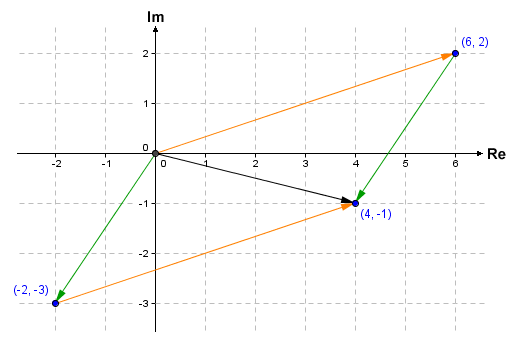
Displacement vectors can also be used for subtraction
Multiplication
A complex number can be multiplied by a real number to give a result that is another complex number. All we need to do is multiply both the real part and the imaginary part of the complex number by the real number. To multiply the complex number a + bi by the real number n, we use the formula:
(a + bi) n = an + bni
Multiplying a complex number by another complex number is slightly more involved, but it is still relatively straightforward. Essentially, each part of the first complex number is multiplied by each part of the second. Let's suppose that we have two complex numbers, a + bi and c + di, for which we want to find the product. We could of course use the standard FOIL method (Firsts, Outers, Inners, Lasts) used to multiply two binomial expressions together like this:
(a + bi)(c + di) = ac + adi + bci + bdi 2
Note, however, that the term i 2 is by definition equal to minus one (-1), so we can streamline the formula somewhat to get the following:
(a + bi)(c + di) = (ac - bd) + (ad + bc)i
Bearing in mind that an imaginary number is just a complex number with a real part that is equal to zero, let's see what happens if we use this method to find the square of the imaginary number i (the imaginary unit, equal to √-1). We should of course achieve a result of minus one - but how does that work out? Here is the calculation:
(0 + 1i )(0 + 1i ) = ((0)(0) - (1)(1)) + ((0)(1) + (1)(0))i = -1
So effectively, we have proved that far from being imaginary, the so-called imaginary unit actually does exist - or at least it does while we are playing by the rules of the complex number system.
We can also multiply together the polar coordinates of two complex numbers to obtain the algebraic expression of their product. We have seen above that a complex number z = x + yi can be expressed in terms of its polar coordinates as:
z = r(cos φ + i sin φ)
To find the product of two complex numbers z1 and z2 for which we have the polar coordinates, we can use the following formula:
z1z2 = r1r2(cos (φ1 + φ2) + i sin (φ1 + φ2))
where r1 and φ1 are respectively the modulus and argument of the complex number z1, and r2 and φ2 are the modulus and argument of the complex number z2.
Multiplying a complex number z = a + bi by successive powers of i produces some interesting results. Here is what happens when we multiply z by powers of i ranging from i -4 through i 4:
zi -4 = (a + bi) i -4 = a + bi
zi -3 = (a + bi) i -3 = -b + ai
zi -2 = (a + bi) i -2 = -a - bi
zi -1 = (a + bi) i -1 = b - ai
zi 0 = (a + bi) i 0 = a + bi
zi 1 = (a + bi) i 1 = -b + ai
zi 2 = (a + bi) i 2 = -a - bi
zi 3 = (a + bi) i 3 = b - ai
zi 4 = (a + bi) i 4 = a + bi
If you continue to multiply z by successive negative or powers of i, the results will simply continue to cycle through the same four complex number values. If we represent z as a point in the complex plane, we can see that multiplication of z by successive powers of i has the effect of rotating that point around the origin in increments of ninety degrees (90°). For positive powers of i the rotation is anti-clockwise, while for negative powers of i the rotation is clockwise. If you have read the page on imaginary numbers, you will realise that this cyclic behaviour is due to the fact that i n = i (n mod 4). You can see below what happens when we multiply the complex number 3 + 2i by successive powers of i. The results are represented as points in the complex plane.
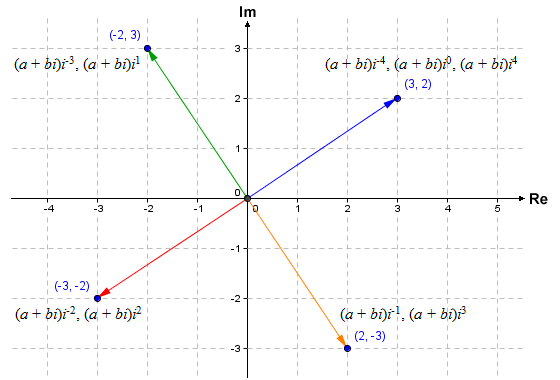
Multiplication of 3 + 2i by successive powers of i
Division
Just as we can multiply a complex number by a real number, we can also divide a complex number by a real number to give a result that is another complex number. All we need to do is divide both the real part and the imaginary part of the complex number by the real number. To divide the complex number a + bi by the real number n, we use the formula:
| a + bi | = | a | + | b | i |
| n | n | n |
The algebraic formula for dividing one complex number by another complex number is somewhat more involved than multiplying two complex numbers together. Let's suppose we want to divide the complex number a + bi by the complex number c + di. Here is the formula we use to do this:
| a + bi | = | (ac + bd) + (-ad + bc) i |
| c + di | c 2 + d 2 |
An example should serve to demonstrate how this works. Let's suppose we want to divide the complex number 2 + 3i by the complex number 4 - 5i. Applying the above formula, we get:
| 2 + 3i | = | ((2)(4) + (3)(-5)) + (-(2)(-5) + (3)(4)) i | = | -7 | + | 22 | i |
| 4 - 5i | 4 2 + 5 2 | 41 | 41 |
We can simplify this formula somewhat by using the complex conjugate, which we saw above. We can achieve the same result by multiplying both the numerator (2 + 3i) and the denominator (4 - 5i) by the conjugate of the denominator (4 + 5i). If we do this, we get:
| (2 + 3i )(4 + 5i ) | = | 8 + 10i + 12i - 15 | = | -7 | + | 22 | i |
| (4 - 5i )(4 + 5i ) | 16 + 20i - 20i + 25 | 41 | 41 |
To find the quotient of two complex numbers z1 and z2 for which we have the polar coordinates, we can use the following formula:
| z1 | = | r1 | (cos (φ1 - φ2) + i sin (φ1 - φ2)) |
| z2 | r2 |
where r1 and φ1 are respectively the modulus and argument of the complex number z1 (the numerator), and r2 and φ2 are the modulus and argument of the complex number z2 (the denominator).
Powers of complex numbers
When a complex number z is raised to the power of a positive integer n, the algebraic formula for calculating the value of zn essentially involves multiplying together n instances of z. This can get very messy as the value of n increases. To illustrate the point, here are the formulae for z2, z3, z4 and z5:
z2 = (x2 - y2 ) + (2xy) i
z3 = (x3 - 3xy2 ) + (3x2y - y3 ) i
z4 = (x4 - 6x2y2 + y4 ) + (4x3y - 4xy3 ) i
z5 = (x5 - 10x3y2 + 5xy4 ) + (5x4y - 10x2y3 + y5 ) i
Fortunately there is a far more elegant way of calculating the nth power of a complex number using polar coordinates. We saw above that a complex number z = x + yi can be expressed in terms of its polar coordinates as:
z = r (cos φ + i sin φ)
There is a formula, sometimes called de Moivre's formula or de Moivre's theorem after the French mathematician Abraham de Moivre (1667-1754) which states that for any complex number z and real value n, we can say:
(cos z + i sin z)n = cos (nz) + i sin (nz)
Proof of this theorem was provided by de Moivre himself for all positive integers. In 1749, the Siwss mathematician and physicist Leonhard Euler (1707-1783) proved that the formula worked for any real value of n. We can therefore use a generalisation of de Moivre's theorem to derive the following formula, which allows us to find the nth power of any complex number:
zn = rn (cos nφ + i sin nφ)
where r and φ are respectively the modulus and argument (i.e. the polar coordinates) of the complex number z. Of course, using this method does entail first finding the modulus and argument of the complex number, but the calculations involved are relatively trivial. Let's try an example. Supposing we want to find z5 for the complex number z = 2 + 3i. We will use the corresponding algebraic formula first:
z5 = (x5 - 10x3y2 + 5xy4 ) + (5x4y - 10x2y3 + y5 ) i
z5 = (32 - (10)(8)(9) + (5)(2)(81)) + ((5)(16)(3) - (10)(4)(27) + 243) i
z5 = (32 - 720 + 810) + (240 - 1080 + 243) i
z5 = 122 - 597i
Before we use the alternative formula to find z5, we need to find the polar coordinates (i.e. the modulus r and the argument φ) of z = 2 + 3i:
r = |z| = √(x2 + y2) = √(4 + 9) = √13 = 3.606
φ = arg(z) = arctan ( 3/2 ) = 56.310°
We can now use the polar coordinates to find z5:
z5 = r5 (cos ((5)( 56.310)) + i sin ((5)( 56.310)))
z5 = 3.6065 (0.200 - 0.980i ) = 122 - 597i
Note that we have shown the results of intermediate calculations rounded to the nearest three decimal places. In order to achieve an accurate result when using a calculator, we suggest that these intermediate results are used without being rounded up or down. For low values of n, finding the nth power of a complex number using polar coordinates may involve the same amount of work (or maybe a little more) as using the corresponding algebraic formula. For larger values of n, however, using polar coordinates is a more efficient option.
Roots of complex numbers
Finding the nth root of a complex number is somewhat trickier than finding the nth root of a real number. We can find the nth root of a positive real number easily enough using a calculator. The nth root of a negative real number can also be found using a calculator. We simply take the nth root of the corresponding positive number and multiply the result by the imaginary unit i. The nth root of a complex number with a non-zero imaginary part, however, will be another complex number. To obtain the square roots of the complex number a + bi (in which b ≠ 0), we can use the following algebraic formula:
√ (a + bi) = ± (γ + δi )
where:
| γ = | √ | a + √ (a2 + b2 ) |
| 2 |
and:
| δ = sgn (b) | √ | -a + √ (a2 + b2 ) |
| 2 |
Note that the sgn() function simply extracts the sign of a real number (in this case b). The Greek letters used here are gamma (γ) and delta (δ). Note also that √(a2 + b2 ) is the modulus (i.e. the absolute value) of the complex number a + bi.
Once we start talking about the nth roots of a complex number where n is greater than two, things get even more interesting. In fact, the nth roots of a complex number z can be found using the following formula, which utilises the complex number's polar coordinates:
| n√z = n√r | ( | cos | ( | φ + 2kπ | ) | + i sin | ( | φ + 2kπ | )) |
| n | n |
In this formula, k can be any positive integer greater than or equal to zero and less than n, r is the modulus (absolute value) of z, and φ is the argument of z. From the above, you should be able to see that if we are looking for the nth root of a (non-zero) complex number, there will be n possible solutions, all of which will themselves be complex numbers.
The reciprocal of a complex number
The reciprocal of a complex number z (i.e. 1/z ) can be found algebraically, and will be another complex number (we'll call it w) that, when multiplied by z, will give a result of one (1). In other words, given that z = x + yi and w = u + vi, we are looking for a value of w that satisfies the equation:
(x + yi )(u + vi ) = 1
Multiplying out the brackets, we get:
(x + yi )(u + vi ) = (xu - yv ) + (xv + yu ) i = 1
We now have a new complex number, i.e. the product of z and w, for which the real part is equal to xu - yv and the imaginary part is equal to (xv + yu) i. However, since the sum of the real and imaginary parts of this new complex number is one (a real number), then the imaginary part must be equal to zero. This in turn means that the real part must be equal to one. So, we can now derive the following two equations:
xu - yv = 1
xv + yu = 0
Since we know the value of z, and hence the values of x and y, we essentially have a pair of simultaneous equations that we need to solve for u and v, which should not be too difficult. In fact, we will end up with the following:
| u = | x |
| x 2 + y 2 |
and
| v = | -y |
| x 2 + y 2 |
Hence the reciprocal of the complex number z = x + yi can be expressed as follows:
| 1 | = w = u + vi = | x - yi |
| z | x 2 + y 2 |
Note that the final expression above is a fraction in which the numerator is the complex conjugate of z. Remember that the conjugate of a complex number simply negates the sign of the imaginary part of the complex number, giving us:
z = x - yi
Remember also that the absolute value of a complex number z = x + yi is given by:
|z| = √(x 2 + y 2 )
and therefore
|z| 2 = x 2 + y 2
Putting these two things together, we can derive the following alternative expression for the reciprocal of the complex number z = x + yi:
| 1 | = | x - yi | = | z |
| z | x 2 + y 2 | |z| 2 |
