Ellipsoids
An ellipsoid is a three-dimensional shape for which all plane cross-sections are either ellipses or circles. The ellipsoid has three axes which intersect at the centre of the ellipsoid. Each axis is perpendicular to the other two, and the ellipsoid is symmetrical around all three axes. The ellipsoid is frequently described as a three-dimensional analogue of the ellipse. In the diagram below, you can see a general (tri-axial) ellipsoid with its semi-axes a, b and c.
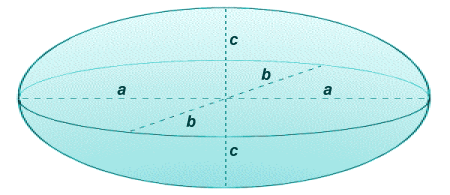
An ellipsoid has three mutually perpendicular axes
There are four distinct kinds of ellipsoid, each characterised by a particular relationship between the semi-axes a, b and c in terms of their relative lengths:
- a > b > c - general or tri-axial ellipsoid
- a = b > c - oblate ellipsoid of revolution (or oblate spheroid)
- a = b < c - prolate ellipsoid of revolution (or prolate spheroid)
- a = b = c - sphere (often referred to as the degenerate case)
We are not really concerned here with the sphere. It is dealt with on the page entitled "The Sphere" in this section. The oblate and prolate spheroids are also of no great interest to us here. They are the subject of the page entitled "Spheroids". The term ellipsoid is most often used to refer specifically to the general (or tri-axial) ellipsoid, for which the semi-axes a, b and c are of different lengths. Semi-axis a belongs to the major axis of the tri-axial ellipsoid, which is the longest. Semi-axis c belongs to the minor axis, which is the shortest, and semi-axis b belongs to the median axis. You can often find pebbles on the beach that are (approximately) ellipsoid in shape.

Beach pebbles are often tri-axial ellipsoids
The formula for the volume of a tri-axial ellipsoid is similar to the formula for the volume of a sphere, except that instead of a single radius, we must consider three distinct semi-axes:
| V = | 4 | πabc |
| 3 |
Calculating the surface area A of a tri-axial ellipsoid is an altogether trickier proposition, especially if accuracy is required. Suffice it to say that the complete formula for the surface area of a tri-axial ellipsoid includes terms of a type called incomplete elliptic integrals of the first and second kind, which are quite as nasty as they sound. The computation required involves integration (one of the major elements in the branch of mathematics known as calculus), and as such is somewhat beyond the scope of this page A reasonable approximation of the surface area of a tri-axial ellipsoid can be obtained using the following formula, first proposed in 2004 by Danish geologist Knud Thomsen:
| A ≈ 4π | apbp + apcp + bpcp | 1/p |
| 3 |
where a value for p of 1.6075 (suggested by Thomsen) will give a reasonably accurate result, although the answer is subject to a margin of error of just over one percent.
