Incidence of Points, Lines and Planes
Overview
It is probably a good idea to clarify exactly what we mean by the term incidence in the context of geometry. When reading through other pages in this section, or when reading other texts dealing with topics related to geometry, you may have come across the term coincidence. Two lines are said to be coincident, for example, if they both pass through the same two points. It effectively means they are the same line. If two circles have radii of different lengths but the same centre, their centres are said to be coincident. If two planes have three points in common that do not lie on a straight line, then they are coincident, i.e. the same plane (remember a plane is a flat, two-dimensional surface that extends to infinity in both directions along each axis).
What, then, is incidence? Put simply, it is a partial coincidence. Two lines that intersect at a single point are not coincident, but they have that single point in common. Because of that, they are said to be incident to one another. A line that passes through a point is said to be incident to that point. A line that passes through a plane at a single point is said to be incident to that plane. And a plane that intersects another plane is said to be incident to that other plane (as you can probably appreciate, the intersection of two planes occurs along a line, rather than at a single point). Incidence is implied by statements such as "point P lies on line l" and "line a intersects line b" and so on.
The title of this page is "Incidence of Points, Lines and Planes". You might have asked yourself, therefore, whether the most trivial case of incidence would involve two points, one incident upon the other. This would, however, necessarily involve the two points having the same x and y coordinates (in the case of a two-dimensional environment) or the same x, y and z coordinates (in the case of a three-dimensional environment). If this were the case, the two points would by definition be coincident rather than incident. Incidence can thus occur between a point and a line, between a point and a plane, between two lines, between a line and a plane, or between two planes, but not between two points.
There are a number of axioms (called the axioms of incidence) relating to the incidence of points, lines and planes. An axiom is a statement or proposition that is accepted as being self-evidently true without requiring mathematical proof, and may therefore be used as a starting point from which other statements or propositions can be derived. The axioms of incidence come in two basic flavours. The first group of axioms we shall look at deal with the relationships between points and lines in a plane (i.e., in a two-dimensional space). The second group deals with relationships between points, lines and planes in a three-dimensional space. In the following sections, we will attempt to explain the implications of each of these axioms.
Incidence relations in a plane
Planar geometry is concerned with objects that have at most two dimensions (such as the plane itself, and any two-dimensional shapes that exist on that plane). Points are dimensionless, since although they are defined by fixed x and y coordinates on the plane relative to some point of origin, they do not themselves have a physical existence. Lines are considered to be one-dimensional, since although the line does not have any real substance (it can be considered to consist of an infinite number of points) it does at least have length. In fact, by definition, the length of a line is infinite. A plane is a flat, two-dimensional surface.
In the broadest sense, the term incidence geometry refers to an area of mathematics that involves the study of incidence relations that can exist between points, lines, planes, and other geometrical entities. In a narrower sense, the term is often used to describe a finite plane geometry (i.e. one defined by a finite number of points and lines). We will concern ourselves here only with the idea of a Euclidean plane (i.e. one that extends to infinity in each of its two dimensions). The basic incidence axioms of planar geometry are set out below.
- For any two distinct points on a plane, there exists one, and only one line that will pass through both points
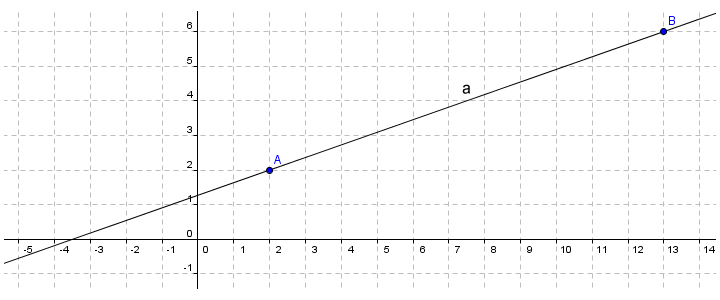
Line a is the only line in the plane that passes through both point A and point B
In the above illustration, line a passes through point A and point B. Line a is unique, because no other line passes through both of these points. The line can be said to be incident with both point A and point B. We could in fact take any pair of distinct points that lie on line a and use them to uniquely define the line. This provides endless possibilities, since by definition a line has infinite length, and there are therefore an infinite number of points on line a.
- If two lines on a plane intersect, they do so at exactly one point and one point only
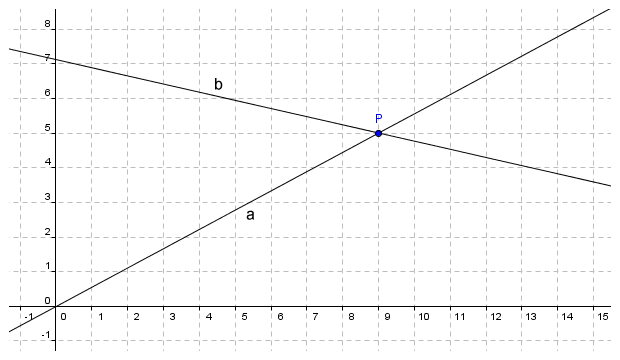
Line a and line b intersect only at point P
Two lines on the same plane that do not intersect are by definition parallel (i.e. at any point along their length, the shortest distance between them will be the same). Conversely, if two lines on the same plane are not parallel, then they will intersect at a single point on the plane. That point will be the only point with which both lines are incident.
- For a line a, and a point P that is not incident with a, there will be exactly one line and one line only that is incident with point P but does not intersect line a
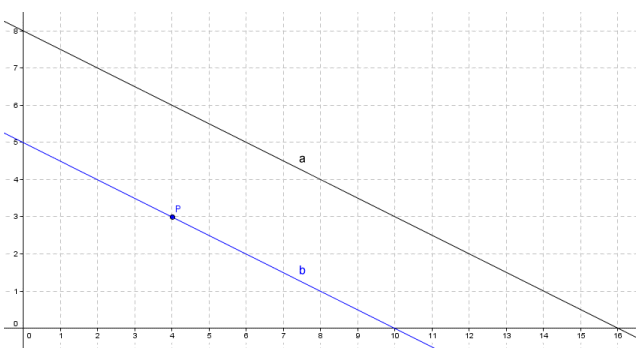
Line b is the only line that is incident with point P that does not intersect line a
In the above illustration, line b passes through (i.e. is incident with) point P, but does not intersect line a, because it is parallel with it. No other line that lies in the same plane as line a can pass through point P without intersecting line a. By definition, two parallel lines in a Euclidean plane never meet. The study of plane geometry can be extended, however, to allow for the possibility of two parallel lines eventually meeting at infinity. A two dimensional plane that allows such a possibility is called a projective plane. Although we are not concerned here with a study of the projective plane, it is interesting to note that the idea of parallel lines meeting at infinity is believed to have originated during the Renaissance, when artists were developing techniques for adding perspective to their drawings (basically to take account of the kind of visual effect that makes it appear that railway tracks converge at some perceived "vanishing point").

Parallel lines converge at a common "vanishing point"
Incidence relations in three-dimensional space
A three dimensional space also contains points and lines. Unlike a two-dimensional space (such as our Euclidean plane), a three-dimensional space can also contain many planes. In fact, a plane in a three-dimensional space is analogous to a line in a two-dimensional space in the sense that two planes are either parallel with one another or intersect one another. On the other hand, lines may be non-parallel but not intersect one another, and both lines and points can be coincident with many different (intersecting) planes simultaneously. As you have probably realised, there are a significantly greater number of possibilities when it comes to incidence relations in three-dimensional space. There are, however, some basic axioms that can be assumed for three-dimensional space:
- For any two distinct points in space there exists one, and only one line that will pass through both points (essentially the same situation that exists for two points in a plane)
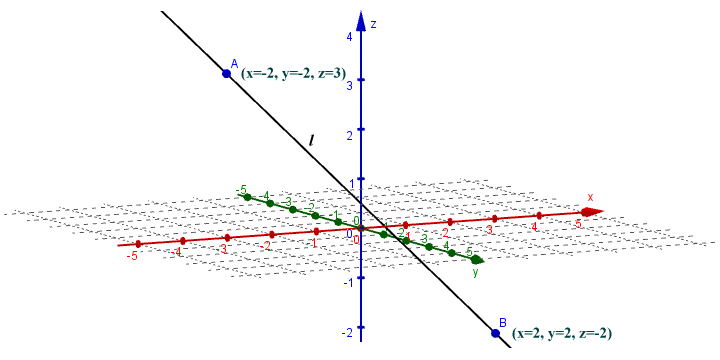
There exists only one line that intersects both point A and point B
In the diagram above, point A has the coordinates x = -2, y = -2, z = 3. Point B has the coordinates x = 2, y = 2, z = -2. Line l is the only line that passes through both points. In two-dimensions, a line must lie totally within the plane in order to exist. This means that all the points that make up the line also lie completely within the plane. It also means that for any line that passes through two points in a plane, the line must also lie completely within the plane. The relationship between lines and planes in a three-dimensional space is obviously going to be more complex. There are in fact three possibilities pertaining to lines in a three-dimensional space:
- the line lies totally within the plane
- the line is incident with the plane at a single point
- the line and the plane do not intersect (they are parallel)
The previous figure shows a three-dimensional space defined by x, y and z axes. By definition, any pair of axes will intersect one another at right angles, and there will be a single plane that contains both axes. The plane containing both the x and y axes is depicted in the figure as a grid. Line l is incident with the plane at a single point. The y axis is also incident with the plane, and with each of the other two axes, at a single point. It is also perpendicular to the plane and both of the other two axes. We can thus see two examples of lines that lie within a plane (the x and y axes) and two examples of lines that intersect the plane at a single point (the z axis and line l). The diagram below shows the same plane as before. This time point A has the coordinates x = -2, y = -1, z = 3, while point B has the coordinates x = 2, y = 1, z = 3. Line l passes through both points, and is parallel with the plane by virtue of the fact that the z coordinates for both points are the same.
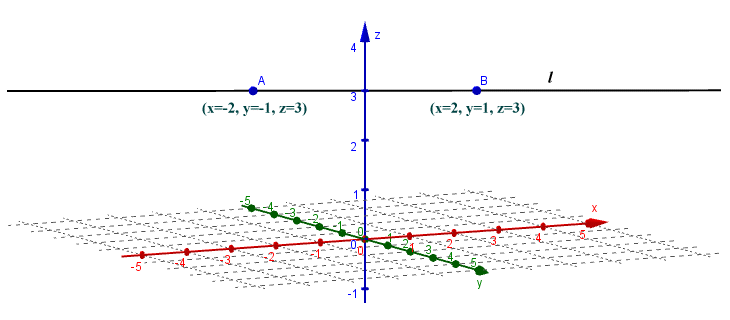
Line l does not intersect the plane that contains the x and y axes
What else can we say about lines and planes in a three-dimensional space? We can say that if two lines intersect, they are incident at precisely one point. That is true in both two and three dimensions. We can also say that there exists one plane, and only one plane, that contains both lines. If two lines do not intersect, there are two possibilities:
- both lines lie in the same plane, and are parallel
- no one plane contains both lines (the lines are said to be skew)
In the example above, line l is parallel with the plane that contains the x and y axes, but is skew with the x and y axes themselves. There will however be many lines that are contained by the plane that are parallel with line l. In the illustration below, points A and B have the same coordinates as previously. Point C has the coordinates x = -2, y = -1, z = 0, while point B has the coordinates x = 2, y = 1, z = 0. Line m passes through points C and D and lies completely within the plane containing the x and y axes. Note points C and D have the same x and y coordinates as points A and B respectively. In fact, for any point on line m, there will be a corresponding point on line l that has the same x and y coordinates. Line m will therefore be parallel to line l. We can infer from this that there exists a plane that contains both line l and line m (this plane will in fact be perpendicular to the plane containing the x and y axes, and intersect it along line m).
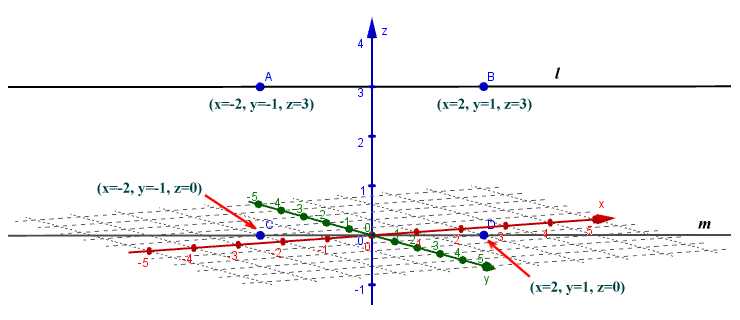
Line l is parallel with line m
There are a few other things that you should appreciate about the relationship between lines, points and planes in a three dimensional space.
- for any three points that do not all lie on the same line, there exists one (and only one) plane that contains all three points
- for any line and some point that does not lie on that line, there exists one (and only one) plane that contains both the line and the point
- given any four points that do not all lie on a single plane, there is no one line that contains more than two of the points
The first of these axioms pretty much implies the second, since for any two of the points there will be a unique line that passes through both of them. The logic behind the last of the three axioms may not be quite so easy to appreciate. The illustration below might help to show how it works. Points A, B and C all lie in the plane containing the x and y axes. Point P does not. The lines containing each possible pairing of two points have been constructed, and none of the lines are incident with more than two points. Note that if point C were to be moved so that it was on the same line as points A and B (in an attempt to prove the rule incorrect), there would in fact exist a plane that contained all four points, since we would have effectively reduced the geometry to one containing a line, and a point not on that line.
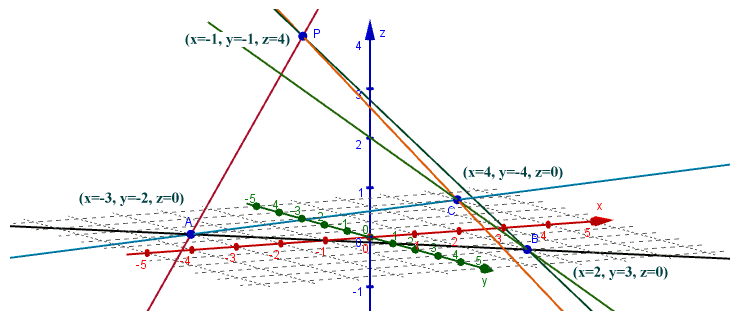
No line is incident with more than two of the points
In a three-dimensional space it is obviously possible to have any number of planes (an infinite number, in fact). The relationship between planes in space is analogous to that between lines in a plane. The planes will either intersect one another or be parallel to one another. The difference, as mentioned earlier, is that whereas two lines intersect at a single point, two planes intersect along a line as shown below. The (finite) planes shown here are perpendicular to one another. Note however that in theory, any number of planes may intersect each other along the same line.
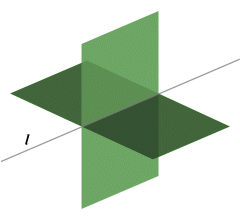
Two planes intersect along line l
For two Euclidean planes in space, there are only two possibilities. The planes either intersect one another along a line, or they are parallel. From this we can infer that if two planes share a point in common, that point must also lie on the line of intersection. Conversely, every point on the line of intersection is shared by both planes. The following illustration shows three (finite) planes that are parallel to one another.

Three planes in parallel
Two more axioms pertaining to planes are worth a mention here, and describe the relationship between planes and lines that are perpendicular to them:
- Two lines that are both perpendicular to the same plane must be parallel
- Two planes that are perpendicular to the same line must be parallel
