Spheroids
A spheroid is a three-dimensional shape that can look like either a stretched or a flattened sphere. A spheroid is the shape that is traced out by rotating an ellipse about one of its two main axes. If the ellipse is rotated about its major axis, the resulting spheroid is called a prolate spheroid, and it looks something like a rugby ball or an American football. If the ellipse is rotated about its minor axis, the resulting spheroid is called an oblate spheroid, and it looks more like a Frisbee (if you are unfamiliar with the characteristics of ellipses, it might be helpful to have a look at the page entitled "Ellipses"). Note that a sphere is a special case of the spheroid for which the ellipse used to generate the spheroid is a circle.

A Frisbee (left) is an oblate spheroid, while a rugby ball (right) is a prolate spheroid
A spheroid has three axes, as shown in the diagram below. Two of the axes (called the equatorial axes) will always be the same length. Each semi-axis of the equatorial axes is an equatorial radius of the spheroid. The equatorial radius is denoted by the letter a. The third axis is called the polar axis of the spheroid. Each semi-axis of the polar axis is a polar radius of the spheroid. The polar radius is denoted by the letter c. For an oblate spheroid, the polar radius will be shorter than the equatorial radius (c < a), and for a prolate spheroid, it will be longer (c > a). If the polar radius and equatorial radius are the same length (c = a), the spheroid must be a sphere.
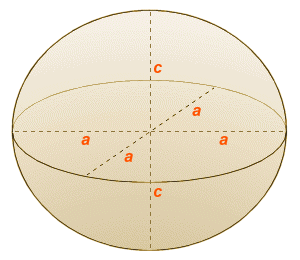
The semi-axes of a spheroid
The volume V of a spheroid (regardless of whether the spheroid is oblate or prolate) is a function of the equatorial and polar radii (a and c). The formula for finding the volume is given below. You may notice that this formula is very similar to the formula used to find the volume of a sphere. In fact, if the spheroid were a sphere, the polar radius c would be the same length as the equatorial radius a. We could simply replace both variables with the radius r of the sphere, and the term πa 2c would be replaced by πr 3.
| V = | 4 | πa 2c |
| 3 |
The surface area A of a spheroid can also be found using a (relatively) straightforward formula. However, there's a catch. The surface area of a spheroid is a function of the equatorial radius, the polar radius, and the ellipticity of the spheroid. The ellipticity (usually denoted as e) is analogous to the eccentricity of an ellipse. Just as the eccentricity of an ellipse is an indication of how much the ellipse deviates from being a circle, so the ellipticity of a spheroid is a measure of how much the spheroid deviates from being a sphere. And that's where you need to be careful, because the ellipticity is calculated differently for oblate and prolate spheroids.
Before we go any further, let's examine the ellipticity, and a couple of other terms relating to the ways in which a spheroid deviates from a sphere. The first term we will look at is called flattening or oblateness, usually denoted as ƒ. As the name suggests, this is a measure of the degree to which the spheroid has been flattened, and is given by the ratio of the difference between the equatorial and polar radii (a - c) and the equatorial radius a. The formula used to obtain the value of ƒ is:
| ƒ = | a - c | = 1 - | c | ( = 1 - c:a ) |
| a | a |
The ratio c:a is the ratio of the length of the polar radius c to that of the equatorial axis a. This ratio is known as the aspect ratio of the spheroid. Obviously, for a prolate spheroid the polar radius would be longer than the equatorial radius. This would give an aspect ratio with a quotient greater than one, and a negative value for ƒ. This is as you might expect, since under these circumstances the spheroid would then be stretched along its polar axis instead of being flattened. Staying with the oblate spheroid for the moment, however, here is the formula for the ellipticity of an oblate spheroid:
| e = √ | ( | a2 - c2 | ) | = √ | ( | 1 - | c2 | ) |
| a2 | a2 |
Factorising the term inside the brackets, we get:
| e = √ | (( | 1 - | c | ) | ( | 1 + | c | )) |
| a | a |
The relationship between e and ƒ can thus be written as:
e = √(ƒ(2 - ƒ))
or conversely:
ƒ = 1 - √(1 - e2)
Don't worry too much if you can't follow exactly how this relationship is derived. The important thing to remember is that the ellipticity of an oblate spheroid (i.e. the degree to which it deviates from being spherical) is directly related to the degree of flattening exhibited by the spheroid in a way that we can quantify algebraically. Once we have obtained the value of e for an oblate spheroid, we can use the formula below to find the total surface area A of the spheroid. Note that ln means the natural logarithm. There should be a function key on your calculator labelled ln that will return the natural logarithm of whatever value is displayed.
| A = 2πa2 + π | c2 | ln | ( | 1 + e | ) |
| e | 1 - e |
Unfortunately the formula for finding the surface area of an oblate spheroid won't work for a prolate spheroid. It is worth noting at this point that there are a number of formulae that can be used to calculate the surface area of spheroids, but there is no single simple formula that works for all three possible types of spheroid (i.e. the oblate spheroid, the sphere, and the prolate spheroid). The sphere, of course, has its own very straightforward formula for the surface area. For the prolate spheroid, we can use the formula shown below, which uses the arcsine trigonometric function. This will probably be labelled on your calculator as sin-1. Note that you should use the arcsine value in radians, and not degrees.
| A = 2πa2 | ( | 1 + | c | sin -1e | ) |
| ae |
Before you can use this formula, you will first need to find the ellipticity e of a prolate spheroid, which is given by the formula:
| e = √ | ( | c2 - a2 | ) | = √ | ( | 1 - | a2 | ) |
| c2 | c2 |
