Measuring Angles
Angles can be measured in either degrees or radians. A full rotation consists of three hundred and sixty degrees (360°), or 2π radians. Each degree can be subdivided into sixty minutes (or arc minutes), and each minute can be further subdivided into sixty seconds (or arc seconds). For the purposes of the following discussion, we will assume that you are familiar with the different types of angle and their properties. If you wish to refresh your memory on the subject of angles, it is dealt with in some detail in the page entitled "Angles" (what else!) in the Geometry section of this website.
Being able to measure angles is a very important skill in fields such as construction and engineering. In fact, it is an essential component of numerous activities, surveying, cartography (map making), woodworking, metalworking, various manufacturing processes, and even the targeting of artillery. Prior to the advent of the Global Positioning System (GPS), being able to measure angles was also vital for the navigation of ships and aircraft. In the field of astronomy, the ability to measure angles accurately and precisely enables us to calculate the position and relative movement of the stars and galaxies in relation to each other, to determine how far distant they are from us, and even to estimate their relative size.
Most people have probably used a protractor at some time in their lives to measure angles on a plan, diagram or drawing. The most common kind of protractor is semi-circular in shape, and made of a clear plastic material. The illustration below shows a typical protractor. Note that the angles from 0° to 180° are marked around the edge of the protractor.
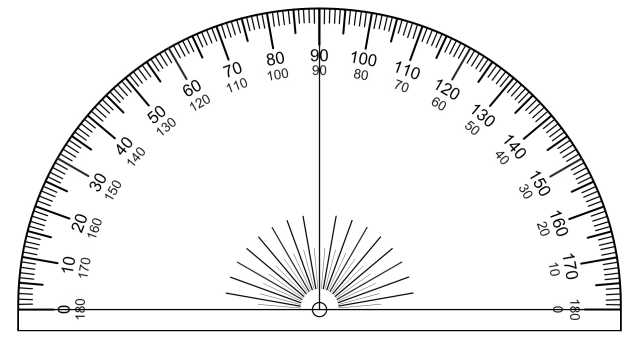
A typical protractor
In order to use the protractor to measure an angle, you place the midpoint of the protractor (i.e. the point where the vertical line from the 90° mark meets the protractor's baseline) over the vertex of the angle. One side of the angle must then be aligned with the baseline of the protractor. Now look at the point where the other side of the angle crosses the numbered scale on the outer edge of the protractor, and read off the value of the angle in degrees. Note that in the illustration above, the scale is marked from zero to one hundred and eighty degrees in both the clockwise and anti-clockwise directions. The scale you need to use will depend on how the angle is drawn, and how you place the protractor. A very nice interactive animation illustrating the use of a protractor to measure an angle can be found on the Math Open Reference website here.
