| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The idea of "computing" – in the broadest sense of the word – is not new. Even in prehistoric times, human beings would have used various methods, including the use of fingers and toes, to count things like the number of sheep or cattle they owned. When the numbers involved were greater than the number of fingers and toes available, or when a more permanent record of some kind was needed, other methods had to be found. Such methods included the use of small stones or pebbles for counting, and the use of notched sticks or knotted chords for recording a quantity.
The Incas used accounting systems that employed ropes and pulleys. These systems were probably the earliest form of binary computer, and used knots in the ropes to represent the binary digits. They were used for tax and government records, and stored information about all of the resources of the Inca Empire, allowing efficient allocation of resources in response to disasters such as storms, drought, and earthquakes. All but one of these systems was destroyed by Spanish soldiers acting on the instructions of Catholic priests, who believed that they were the work of the Devil.
Probably the first serious effort to build computing machines was made by the Greeks, who built analogue and digital computing devices that used intricate gear systems, although they were subsequently abandoned as being impractical. One computing device that has survived, despite having its origins in the ancient world, is the counting frame, more commonly known as the Abacus. Not only have numerous examples of this device survived, it is still in use today in one form or another in many parts of the world.
Opinions seem to differ as to when and where the abacus first came into being. There is certainly evidence to suggest that various forms of counting board were in use in some parts of the world thousands of years ago. The counting board was a simple counting device, usually made from stone or wood. These boards usually had shallow grooves to accommodate small pebbles or beads. The grooves were usually accompanied by markings that indicated the magnitude of the values they represented.
The oldest surviving example of a counting board, the Salamis Tablet, was discovered on the Greek island of Salamis in 1899 and is thought to date from around 300 BCE. It currently resides in the Epigraphical Museum in Athens. Constructed from marble and with approximate dimensions of 150 x 75 x 4.5 centimetres, it can hardly be considered a portable computing device. Indeed, it is not entirely clear whether or not it would have been used for carrying out calculations or, as some sources suggest, as some kind of gaming board.
There is evidence to suggest that counting boards were used by the Persians from around 600 BCE, and by the Greeks from approximately 500 BC. These devices were undoubtedly the precursor to the abacus. According to the Greek historian Herodotus (circa 484 – 425 BCE), counting boards were also in use in ancient Egypt.
The earliest use of a counting frame (as opposed to a counting board) probably occurred in China, where its use is recorded in documentation dating from the 2nd century BCE. The Chinese abacus (or suanpan) has a rectangular wooden frame, with a number of bamboo rods (usually seven or more) mounted vertically within the frame.

Graphical representation of a Chinese abacus (Suanpan)
As you can see from the illustration, a horizontal bar divides the frame into an upper deck and a lower deck. Each rod typically carries seven beads or discs – two on the upper deck and five on the lower deck. The beads in the upper deck are sometimes referred to as "heaven beads" and each bead has a value of five (5). Those in the lower deck may be referred to as "earth beads" or "water beads", and each has a value of one (1).
Each column, usually starting from the right-most column, represents successive powers of ten, starting with 100 (i.e. 1). Calculations are carried out by moving beads towards or away from the horizontal bar. The result of a calculation is represented by the beads closest to the horizontal bar, on both decks, once the calculation has been completed. The number represented by the suanpan in the illustration is 70,710,678.
Those trained in the use of the suanpan can often carry out calculations involving large numbers just as quickly (and sometimes even faster!) than someone using a calculator. We’re not going to go into a lengthy session on how to use the device in this article, but we’ll look at a very simple example. Let’s suppose we want to add the numbers seven (7) and two (2).
We start by clearing the frame, which we do by placing it flat on an even surface and moving all of the beads away from the horizontal divider bar, so that all of the beads in the upper deck are moved as far as they will go towards the top of the frame, and all of the beads in the lower deck are moved as far as they will go towards the bottom of the frame. This is the equivalent of pressing the "clear" button on a calculator!
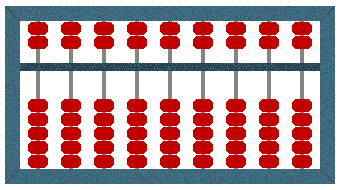
The Suanpan is cleared
To perform the addition, we simply need to count the beads for the first number, then count the beads for the second number. To count the first number (7), we move one bead from the upper deck of the right-most column (the upper deck beads are worth five, remember) and two beads from the lower deck of the right-most column (each worth one) towards the bar.
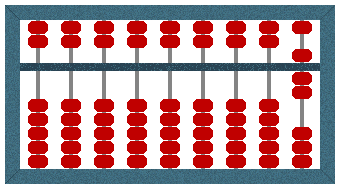
The Suanpan displays a value of 7
To count the second number (2), we move a further two beads from the lower deck of the right-most column towards the bar.
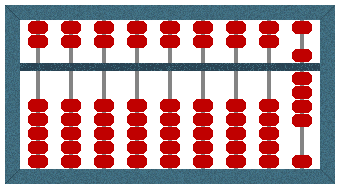
The Suanpan displays a value of 9
We find the answer to a calculation by adding up the values of the beads adjacent to the bar in each column. In this case, only the first column is involved in the calculation. We have one bead in the upper deck worth five (5), and four beads in the lower deck worth one (1) each, giving a total of nine (9). This example is admittedly quite trivial, and one that you could undoubtedly do in your head, but it demonstrates the principle.
Subtraction can be carried out just as easily. If, for example, we want to subtract three (3) from the result of our previous calculation, we simply move three of the beads in the lower deck of the right-most column away from the bar. This leaves us with one bead in the upper deck worth five (5), and one bead in the lower deck worth one (1), giving a total of six (6) – which is the correct answer to nine minus three (9 – 3).
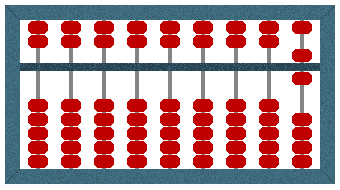
The Suanpan displays a value of 6
If a counting operation carried out during an addition results in a value of greater than ten (10) on any wire, a "carry" is accomplished by clearing beads from the upper and lower decks of the wire (the beads cleared should have a combined value of ten), and moving one bead from the lower deck of the wire immediately to the left of the affected wire towards the bar.
Many operations require an understanding of what are known as complementary numbers. In this instance, we are referring to any two numbers less than ten that, when added together, add up to ten (i.e. 9 + 1, 8 + 2, 7 + 3, 6 + 4 and 5 + 5). Suppose, for example, we want to add three and eight (3 + 8). First, we "reset" the abacus, then we set it to three by moving three beads in the lower deck from the 1’s column (the right-most wire) towards the bar.
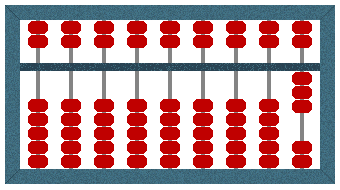
The Suanpan displays a value of 3
We want to add eight to this number, so we start by subtracting two (two is the complement of eight) by moving two of the beads we originally moved away from the bar.
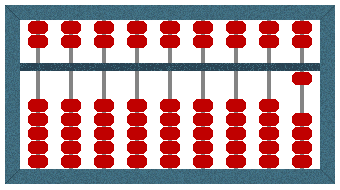
The Suanpan displays a value of 1
We complete the operation by moving one bead in the lower deck from the 10’s column (the second right-most wire) towards the bar. This leaves us with one bead from the 10’s column and one bead from the 1’s column on the bar, which represents a value of eleven (11) – the correct answer.
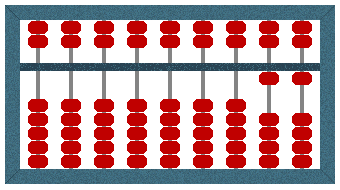
The Suanpan displays a value of 11
Archaeological evidence dating from the first century CE indicates that the Romans developed their own version of the abacus, although in the Roman version the beads ran in grooves rather than on wires. There are also historical sources from the same period indicating that counting frames were in use in India at around the same time.
The suanpan appears to have migrated from China to both Korea (where it is variously called a jupan, jusan or supan) and Japan (where it is known as a soroban) during the fifteenth and sixteenth centuries CE. A Russian version of the abacus (the Schoty) appeared around the end of the sixteenth century CE.
Counting frames of one kind or another were in widespread use in various parts of Western Europe up until around 1500. Use of the abacus in Europe and elsewhere declined rapidly with the adoption of the Hindu-Arabic numeral system, first developed in India some time between the first and fourth centuries CE and later adopted by Arab mathematicians.
The Hindu-Arabic system was a positional decimal numeral system that eventually became the most commonly used system for the symbolic representation of numbers worldwide, and the one we use today. It made record-keeping easier, and facilitated the use of algorithmic methods for performing calculations on paper that were simply more convenient than the use of a counting frame.
Nevertheless, use of the abacus for counting and making calculations continued in some parts of the world and, as we mentioned earlier, persists to this day. The abacus allows a wide range of numbers to be represented, and can be used to perform a range of mathematical operations – addition, subtraction, multiplication and division, and even the calculation of square roots. A skilled operator can often make such calculations faster than someone using a calculator or a slide rule.
One benefit of using an abacus is that, unlike performing calculations using a calculator or pen and paper, it is highly tactile and provides significant visual feedback to the user. For this reason, it is often used in pre-school and elementary education to introduce children to number systems and basic mathematical concepts. Indeed, if you visit your local toy shop, you will probably find an abacus being sold as an educational children’s toy.
Although the counting frame may seem far removed from a modern-day digital computer, it may not be as different as you think. Like a computer, it represents values discretely, which effectively makes it a digital device. It also works on the principle of making repeated calculations to arrive at a result, which is very much the way in which a computer works. Also, like a computer, it arrives at a result much faster than a human being using mental arithmetic alone – at least in the majority of cases.