| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The thing about imaginary numbers is that they are ... well ... not imaginary. At least, they are no more imaginary than the kind of numbers we are more familiar with. They were labelled "imaginary" a very long time ago, when their existence was still not widely accepted. As is often the case, however, the name stuck. The concept of imaginary numbers is thought to have been around since at least the first century CE, when it was supposedly encountered by the Greek mathematician and engineer Heron of Alexandria whilst he was working on a formula for finding the volume of a frustrum (a truncated pyramid).
Very little further attention was paid to the subject of imaginary numbers until the sixteenth century CE, when the Italian mathematician Rafael Bombelli (1526 - 1572) described just about everything that was known about algebra at the time in his book L'algebra, written in 1572. He attempted to write about the subject of algebra in a way that could be understood by anyone, not just mathematicians. Bombelli's book was also significant because in it, he outlined the concept of a complex number system and laid down the rules for arithmetic operations (addition, subtraction, multiplication and division) involving complex numbers. The subject of complex numbers is dealt with in some detail in a separate page. For the moment, you need only be aware that a complex number is made up of two parts - a real part, and an imaginary part (which is probably why it is called a complex number). A complex number takes the form:
(a + bi)
where a and b are real numbers, and i is the imaginary unit (we will say more about i shortly).
Bombelli took the idea of imaginary numbers very seriously, because he realised that they provided the key to solving certain types of equation that could not otherwise be solved. Solving such equations typically involves finding the square root of a negative number - something that simply isn't possible using the real number system with which we are familiar. Try squaring any number you can think of - positive or negative - and the result will always be a positive number. So how on earth do we find the square root of a negative number? To help us understand the answer to this problem, it is useful to think about how our ideas about numbers have evolved.
Most of the mathematical concepts with which we are familiar today have emerged naturally as the result of having to solve some new kind of problem. In primitive societies, people were primarily interested in counting things, like sheep and cattle. To that end, they invented the natural (counting) numbers. At some point in our development (probably not very long after we learned how to count things), we realised that not everything in the world could be quantified in terms of whole numbers. So, we came up with the idea of fractions in order to be able to describe partial quantities like half an apple, or a quarter of an inch. It may seem hard to believe now, but the number zero (0) was not even considered to be a number by the ancient Greeks. In fact, it is first thought to have been accepted as being a number in its own right (as opposed to simply being used as a placeholder) by Indian mathematicians in the ninth century CE, who used it extensively in their calculations.
Like many new ideas, and despite the huge contribution made by Rafael Bombelli, the idea of imaginary numbers was not widely accepted or understood until at least the middle of the eighteenth century CE. Indeed, the term "imaginary" is thought to have been coined by the French philosopher and mathematician René Descartes (1596 - 1650), in the seventeenth century CE, as a derogatory term. It was the Swiss mathematician and physicist Leonhard Euler (1707 - 1783) who first used the letter i to denote the imaginary unit (note that in electrical and electronic engineering, the letter j is used, because i is already in use as the symbol for electrical current). The imaginary unit is a number that, when squared, gives a result of minus one (-1). We can express this concept algebraically as:
i 2 = -1
Obviously, we can only accept the existence of such a number if we are prepared to look beyond the limitations of the real number system. Indeed, imaginary numbers are not a part of the real number system. Rather, they are part of the complex number system that we mentioned earlier. Although we will not discuss the complex number system in any depth here, we have already seen that a complex number is actually a pair of numbers. Although in a sense both of these numbers are real numbers, one of the numbers is designated as the "real" part, and the other is designated as the "imaginary" part. The rules for carrying out arithmetic involving complex numbers are somewhat different to those governing arithmetic involving real numbers. When you read the page on complex numbers, you will see how, using these rules, a complex number with a real part of zero (0) can be the square root of a negative real number. And that, effectively, is what an imaginary number is - a complex number that has a real part of zero.
The imaginary unit i has a similar kind of relationship with other imaginary numbers as the number one has with other real numbers. We could, for example, express any real number as the product of that number and one. For example, the real number six (6) could be expressed as 6 × 1. In the same way, we can express an imaginary number as the product of a real number and i. Imaginary six would be written as 6i. Of course, with real numbers we can just write the number itself. When working with imaginary numbers, we should always include the symbol i to indicate that we are expressing an imaginary number. This will avoid confusion over what kind of number we actually mean.
Imaginary numbers allow us to express the square root of a negative number. All we do is write down the square root of the corresponding positive number, and append the symbol i. Thus, the square root of minus twenty-five (√-25) becomes the product of the square root of twenty-five (√25) and i. We can express this as follows:
√-25 = √25 × i = 5i
Generalising this equation for any number n, we can say:
√(-n) = √n × i = i√n
Once we have a means of expressing the square root of a negative number, we can find the solution to many problems that were previously either impossible or extremely difficult to solve. Whether you are studying engineering, electronics, mathematics or one of the physical sciences, you are guaranteed to come across various types of polynomial equation. Many of these equations will have one or more solutions that involve finding the square root of a negative number. Thanks to our new-found understanding of imaginary numbers, we now have a way of expressing these solutions. As an example, consider the simple quadratic equation x 2 + 1 = 0. Solving for x, we get:
x 2 = -1
x = √-1 = i
If we draw a graph of the corresponding function, as shown below, we can see that there is no real solution, since the graph does not intercept the x-axis:
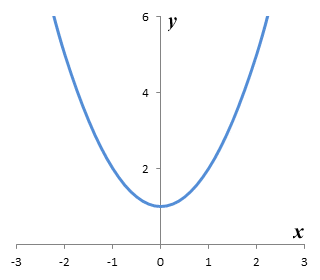
The graph of y = ƒ(x) = x 2 + 1
Of course, if you are familiar with quadratic equations, you will know that every quadratic equation has two solutions. The two solutions may both be the same real number (the equation has what is known as a double root, where the graph of its function touches the x-axis at a single point), or they could be two different real numbers (where the graph intercepts the x-axis at two distinct points). The third possibility is that the solutions are both imaginary numbers (the graph does not intercept the x-axis at all). We can see from the graph that x 2 + 1 = 0 has no real roots. You may be tempted to ask, however, why we only have one imaginary solution. The answer is that we actually have two imaginary solutions. We know that every positive real number has two square roots - the square root of four (4), for example, can be either two (2) or minus two (-2). Exactly the same principle applies to negative numbers - a negative number also has two square roots. In this case, the solution to our equation is the square root of minus one, which can be either i or -i.
In many ways, imaginary numbers behave just like real numbers. For example, we can add and subtract imaginary numbers, as in the following examples:
i + i = 2i
3i + 4i = 7i
5i - 2i = 3i
i - 2i = -i
Note that we cannot add an imaginary number to a real number and get any meaningful result, since they are different kinds of number. We can however multiply imaginary numbers by real numbers:
7i × 4 × 28i
2i × -3 × -6i
-3i × -4 × 12i
We can also divide an imaginary number by a real number:
18i ÷ 3 × 6i
-24i ÷ 6 × -4i
30i ÷ -5 × -6i
Multiplying imaginary numbers together is relatively straightforward. Remember, however, that i 2 is equal to minus one (-1), while i × -i is equal to one (1). Remember also that multiplying an even number of imaginary numbers together always results in a real number, while multiplying an odd number of imaginary numbers together always results in an imaginary number. Here are some examples:
2i × 8i = -16
2i × -3i = 6
4i × -7i × i = 28i
We can also divide one imaginary number by another imaginary number. Be aware, however, that the result will be a real number:
16i ÷ 4i = 16 ÷ 4 = 4
-21i ÷ 3i = -21 ÷ 3 = -7
As you may have already realised, just as squaring a real number (positive or negative) always results in a positive number, squaring an imaginary number (positive or negative) always results in a negative number:
(4i) 2 = -16
(-7i) 2 = -49
We have said that, in essence, i is to imaginary numbers what one is to real numbers. There is an interesting difference, though, when it comes to raising i to some power. If we raise one to an integer power, the result will always be one, regardless of whether the exponent used is a positive integer, a negative integer, or zero. The result of raising i to an integer power, on the other hand, will vary, depending on the exponent used. In fact, as we increase or decrease the value of the exponent, the result will cycle through four different possible values. The following sequence should serve to illustrate what we mean:
i -6 = -1
i -5 = -i
i -4 = 1
i -3 = i
i -2 = -1
i -1 = -i
i 0 = 1
i 1 = i
i 2 = -1
i 3 = -i
i 4 = 1
i 5 = i
i 6 = -1
We could continue listing powers of i indefinitely in both the positive and the negative direction, but the sequence would continue to cycle through the same four values, and in the same order. We can therefore derive the following rule for finding the value of i to any integer power:
i n = i (n mod 4)
In other words, we simply divide the exponent n by four, and take the remainder (n mod 4) as the exponent instead.