| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Real numbers (or just reals) can be thought of as a set of values that represent every possible position on a line that starts at some arbitrary point of origin (which we will call zero) and stretches to infinity in two opposite directions. This number line is typically represented in text books as a horizontal line, as illustrated below. The origin (zero) is shown as a point at the centre of the line. Evenly-spaced points are marked on the line to either side of the origin. The points to the right of the origin represent the positive integers, while the points to the left of the origin represent the negative integers. An arrowhead is appended to each end of the line to show that the line extends indefinitely in both directions.
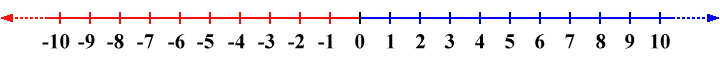
Real numbers are represented as points on an infinitely long number line
The set of real numbers is usually signified using the symbol ℝ (a double-struck R). You have probably already realised that since the positive and negative integers lie on the real number line, then they too must be real numbers. The same is true of zero. By definition, the set of real numbers includes the natural numbers (or counting numbers) and the whole numbers (the set of natural numbers plus zero). It also includes what we call rational numbers and irrational numbers (more about these later). You may well have some questions at this point. For example, why are they called "real" numbers, and what kind of number is not real? The simple answer is that there are such things as imaginary numbers, the subject of which will be dealt with elsewhere. Real numbers only started to be called real numbers because mathematicians needed to differentiate between them and these so-called imaginary numbers.
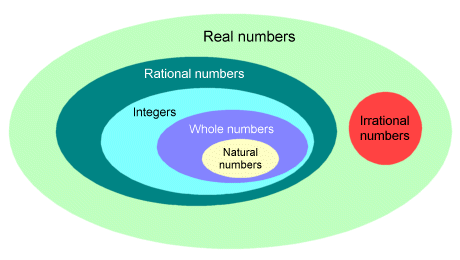
This Venn diagram shows the hierarchy of real numbers
Although we sometimes talk about the set of real numbers, mathematicians more often refer to it in terms of a field or continuum. The word set implies that we are dealing with something that can be counted. When we talk about the set of natural numbers, for example, we know that we can start at one (or zero, depending on how you choose to define the natural numbers) and count to . . . well, infinity. It is of course true that we would never actually finish counting, no matter how long we kept going. Nevertheless, we could continue to count. For that reason, mathematicians tend to describe the set of natural numbers as being countably infinite. In fact, it's not only the natural numbers. Whole numbers, integers and rational numbers are all countably infinite!
"But hang on a minute . . .", I hear you cry, " . . . how on Earth do you count rational numbers? I mean, they're fractions . . . ?". Very true. But they can nevertheless be counted, and we'll see why in due course. So why can't we count the reals? Well, the key word here is continuum. Once you really start to think about this question, you begin to realise intuitively why we can't count the real numbers. Imagine, for example, that we want to start counting positive real numbers, starting with zero. What is the first positive real number after zero? You could spend an awful lot of time thinking about that one! But we'll come back to the question of why rational numbers are countably infinite, whereas real numbers are not, later.
In the meantime, there are some other rather interesting things to consider. It's fairly easy to see that there must be infinitely many real numbers on the number line. At the same time, however, there must also be infinitely many real numbers between any two points on the number line, no matter how close together those points may be. Clearly, not all infinities are equal! All we can say at this point is that there is a paradox here, but it is not one that we need to worry too much about unless, and until, we undertake the study of higher mathematics. For now, it is enough to understand that we cannot count the real numbers in the same way that we can count the natural numbers or rational numbers. They are said to be uncountably infinite. We can therefore also say that the cardinality of the set of real numbers is greater than the cardinality of the set of natural numbers, despite both sets having an infinite number of members.
Real numbers are very useful when we want to measure things in the physical world that vary continuously (as opposed to discretely). Some examples that spring to mind include temperature, voltage, the pressure of a gas, or the density of a liquid. Of course, we often talk about these things in everyday life using integer values. For example, it is sufficient for the purposes of a public weather forecast to give the maximum and minimum temperatures expected on a particular day to the nearest degree. And, let's face it, these predictions are often wrong anyway. In many areas of science and technology, however, we often need to be far more precise. When talking about global temperature variations over a number of years or decades, for example, even small fractions of a degree may be significant. And when we get into areas such as particle physics, the ability to measure unimaginably small differences in things like mass is absolutely crucial. We very much depend on real numbers to enable us to express quantities that constantly vary, especially when the amount by which they vary may be infinitesimally small.
From the Venn diagram we saw earlier, we can see that all real numbers are either rational (including integers, whole numbers and the natural numbers) or irrational. Let's look at rational numbers first. Significantly, the word rational contains the word ratio. When we talk about rational numbers, we are talking about numbers that can be expressed as the ratio of two integer values. One of the ways in which we can express rational numbers is as a fraction. So, any number that we can express as a fraction is a rational number. Fairly obviously, it follows that any number we can't express as a fraction is not a rational number. Many students at this point ask how this can be, when clearly the set of rational numbers includes the integers (and therefore by definition the set of natural numbers, which is a subset of the integers). These numbers, after all, are not fractions. Nevertheless, they can be expressed as the ratio of two integer values. In fact, they can even be expressed as fractions. We just need to use a denominator of one (1). The following table presents some examples of rational numbers, together with their representation as fractions:
| Number | As a fraction |
|---|---|
| 6 | 6/1 |
| √9 | 3/1 |
| 0.375 | 3/8 |
| 1.7 | 17/10 |
| 3.141592 | 392,699/125,000 |
| 0.333r | 1/3 |
| 0.142857142857142857... | 1/7 |
The first number in our table is six (6), and demonstrates how we can represent an integer value as a fraction simply by using the number itself as the numerator, with a denominator of one. The second number is the square root of nine (√9). Since nine is a square number (i.e. the result of multiplying an integer value by itself), we can easily simplify √9 to its integer value (in this case three) and then represent it as a fraction in the same way we did previously with six. The decimal fraction zero-point-three-seven-five (0.375) represents the fraction three hundred and seventy-five over one thousand (375/1,000), but since both three hundred and seventy-five and one thousand can be divided by one hundred and twenty-five (125), we can simplify this fraction to three-eighths (3/8). In similar fashion, we can express the number one-point-seven (1.7) as seventeen-tenths (17/10).
The next example may have given you some pause for thought. Surely this is Pi (π)? Well, yes and no. It is an approximation of Pi. Had we written the actual symbol for Pi, rather than a decimal number that approximates Pi, then it would definitely be out of place in our table of rational numbers. Pi is not a rational number, because it cannot be expressed as the ratio of two integers. At the time of writing, a decimal representation of Pi has been calculated to a precision of over ten trillion (10,000,000,000,000) digits, but this is still only an approximation. Having said that, a value of Pi calculated to just forty significant digits is usually more than adequate, even for the kind of calculations typically carried out by astrophysicists and cosmologists.
Remember that any decimal number that terminates (has a finite number of digits after the decimal point) is rational by definition, since it can be represented as the quotient of two integers. This is true even if the number is being used to represent a non-rational value like Pi. A decimal representation that has either a single digit after the decimal point that repeats forever, or a whole sequence of decimal digits that repeats forever, is also a rational number. The penultimate example in our table, zero-point-three recurring (0.333r), is the decimal representation of one-third (1/3), in which the digit three after the decimal point repeats forever. The letter r here stands for recurring, and simply indicates that the digit which it follows will be repeated forever. In the final example, we see the decimal representation of one-seventh (1/7), in which the sequence of digits one-four-two-eight-five-seven (142857) repeats continuously after the decimal point (the repetition is indicated using ellipsis (...). If, as an exercise, you try dividing one by seven (1 ÷ 7) using traditional long division techniques, you will be able to see how this repeating pattern of digits emerges.
We can formally define a rational number as one that can be represented as the quotient of two integers. In other words, we can say that a rational number is a number that can be expressed in the form p/q, where p and q are integer values, and q is not equal to zero (the result of dividing any number by zero is said to be undefined). In the fifth century BCE, The Greek philosopher and mathematician Pythagoras, together with his followers, believed that everything in the universe could be quantified using rational numbers, i.e. either integers or numbers that could be expressed as the quotient of two integers. This belief is understandable up to a point, since even today we are only able to represent quantities that are not rational using either an abstract symbol, or a rational number that is an approximation of the actual value. Admittedly, these approximations are often calculated with an extremely high degree of precision, but they are still approximations.
For the Pythagoreans, everything in the physical world could be described by, or measured using, rational numbers. This concept was central to their philosophy and religion. Indeed, there is certainly no shortage of rational numbers. There are an infinite number of rational numbers, just as there are an infinite number of natural numbers. Indeed, between any two rational numbers, no matter how close together they are on the number line, we can always find another rational number. In fact, we can find an infinite number of rational numbers between any two rational numbers. We can therefore say that the density of rational numbers on the number line is infinite. At the same time, since we know that there are numbers on the number line that are not rational, there must be gaps in between the rational numbers. We can also say that, like the set of natural numbers, the set of rational numbers (usually denoted using the symbol ℚ - a double-struck Q, for quotient) is countably infinite.
This last concept is somewhat more difficult to grasp than the concept that the set of natural numbers and the set of integers are both countably infinite, but it follows from the fact that we can express any rational number as the quotient of two integer values. A graphical representation may help to clarify matters. Consider the table below, in which we show every possible rational number that can be expressed using pairs of positive integers taken from the number range one to ten, expressed as a fraction. Now consider that we could extend the table to have an infinite number of rows and columns, in both the positive and negative directions. Even in our extended table, both the number of rows and the number of columns can be said to be countably infinite, because we can actually count them (even if the task would be a never ending one). Now, since every rational number that exists must be represented by at least one of the cells in our extended table, then the set of rational numbers must itself be countably infinite. In fact, if you think about it for long enough, you will realise that every rational number is represented by an infinite number of cells in our table!
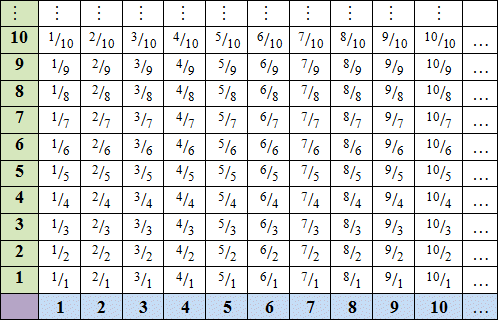
The rational numbers are countably infinite
Any real numbers that cannot be expressed as the quotient of two integers are said to be irrational numbers. We have already stated that the set of real numbers is uncountably infinite, and that the set of rational numbers is countably infinite. Since all real numbers are either rational or irrational, the conclusion must be that there are far more irrational numbers than rational numbers. In fact, it turns out that almost all real numbers are irrational. According to some sources, the Pythagoreans became aware of the existence of irrational numbers thanks to the efforts of one of Pythagoras' students, Hippasus. Although we don't really know that much about Hippasus, one story has it that he discovered the existence of irrational numbers whilst trying to find the length of the diagonal of a unit square (i.e. a square with side lengths of one unit). Far from being celebrated for this discovery, he was allegedly thrown overboard and drowned by some of his fellow Pythagoreans whilst on a sea voyage. They were presumably less than happy that one of their most sacred beliefs - that everything in the universe could be described or measured in terms of rational numbers - had been proved false.
Whether or not there is any truth to the stories about Hippasus, the example of the unit square is as good as any to demonstrate the existence of a number that cannot be expressed as the ratio of two integers - in other words, an irrational number. Consider the diagram below, which shows two adjacent sides of a unit square and one of its diagonals. From Pythagoras' theorem, we know that the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides. In this case, the two legs of the right-angled triangle are two adjacent sides of a unit square, and the hypotenuse is one diagonal of the same unit square. Since the legs of the right-angled triangle are both one unit in length, their squares added together are equal to two (2). The hypotenuse (i.e. the diagonal of the unit square) must therefore be equal to the square root of two (√2). The decimal representation of this value shown in the diagram was obtained using a calculator, which can obviously only show a limited number of digits after the decimal point (in this case, thirty-one digits). The ellipsis after the last digit simply indicates that the sequence of digits continues, but cannot be displayed.
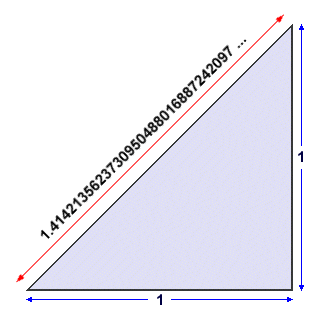
The length of the diagonal of a unit square is an irrational number
One of the defining characteristics of an irrational number is that its decimal representation does not terminate or repeat. In other words, the sequence of digits after the decimal point goes on forever, and contains no regularly repeating pattern. Looking at the decimal representation of √2 displayed by our calculator, there would certainly appear to be no repeating pattern of digits. Of course it is not really possible to say, just from looking at the calculator output, whether or not the sequence of digits would eventually terminate or start to repeat itself. Admittedly it doesn't seem particularly likely, but we need to be certain before we can claim that this number is indeed irrational. As it turns out, we can prove that √2 is not a rational number relatively easily using a little bit of algebra. Let's start with the premise that √2 can be expressed in the form p/q, where p and q are integer values, and q is not equal to zero. We can state this formally as:
| √2 = | p |
| q |
The proof we are looking for relies on the assumption that the fraction p/q is reduced to its lowest form, i.e. it cannot be further simplified. This being the case, then either p or q (or both) must be odd, since if both p and q were even, both the numerator and the denominator would have two (2) as a factor, and the fraction could be simplified further. Let's modify our original equation by squaring it to eliminate the square root:
| 2 = | p 2 |
| q 2 |
Rearranging this equation gives us the following:
p 2 = 2q 2
This means that p 2 must be even, since it is equal to the square of some integer (q) multiplied by two. At this point we should point out, for those of you who did not already know, that squaring an even number always gives us an even number, while squaring an odd number always gives us an odd number. It therefore follows that if p 2 is an even number then p must also be an even number. Furthermore, if p is an even number, it must be equal to two multiplied by some other number. For argument's sake, let's call this other number n, so that p = 2n. Let's modify our equation once more to include this new term:
(2n) 2 = 2q 2
Expanding the term in brackets gives us:
4n 2 = 2q 2
Simplifying and re-arranging gives us:
q 2 = 2n 2
So, p 2 must also be even, since it is equal to the square of some integer (n) multiplied by two. This in turn means that p must also be even, because we have already established that only an even number can be squared to produce another even number.
What have we proved here? We said above that, for a fraction to be in its lowest form, either the numerator or the denominator (or both) must be odd numbers. We have also stated that the fraction p/q (which is the hypothetical representation of √2 as a rational number) is already in its simplest form. Therefore, if √2 really were a rational number, either p or q (or both) would have to be an odd number. However, we have now shown that both p and q in our original equation must be even numbers. That being the case, then the fraction p/q cannot be in its simplest form, since p and q have a common factor (two). The only conclusion we can reach, given this obvious contradiction, is that √2 cannot possibly be represented as the quotient of two integers, and is therefore irrational.
When you think about it, the square root of any number n can only be rational if n is a perfect square, i.e. a number that results from squaring a rational number. This may be stating the blindingly obvious, but saying it serves to underline the fact that any number that is not a perfect square cannot have a rational root.
There are a couple of other things about real numbers - both rational and irrational - that are worth mentioning. First of all, it should be noted that all rational numbers are also algebraic numbers. An algebraic number is any number that can be a root (i.e. a solution) of a non-zero polynomial equation with rational coefficients. To clarify, consider the following polynomial equation:
x 2 - 4x - 5 = 0
This equation satisfies our requirements in terms of having rational coefficients. In this case, the coefficients of the first two terms are one and four respectively (the last term is a constant, and therefore by implication has a coefficient of one). Obviously, since the coefficients in the polynomial are not all equal to zero, it also fulfills the requirement of being a non-zero polynomial. The root (or roots) of the equation will be any value of x that satisfies the equation (i.e. makes it true). In this case, there are two values of x that satisfy the equation - minus one (-1) and five (5). Both of these values are rational numbers. The graph of the polynomial's corresponding function is shown below, and clearly shows the roots of the equation (i.e. the x coordinates of the points at which the graph intercepts the x-axis).
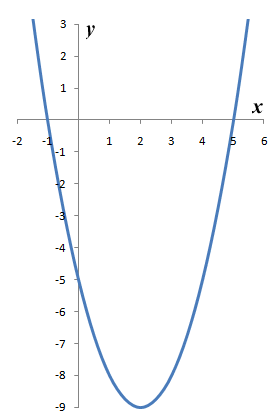
The graph of y = ƒ(x) = x2 - 4x - 5
For every rational number n, there will exist at least one non-zero polynomial equation with rational coefficients that has n as one of its roots. This means that, by definition, every rational number must be an algebraic number. The same cannot be said for irrational numbers. In fact, most irrational numbers are not algebraic numbers. An irrational number that is not an algebraic number is called a transcendental number. This doesn't mean that there is anything mystical about it, just that it cannot be a root of a non-zero polynomial equation with rational coefficients. An example commonly given of an irrational number that is also transcendental is the mathematical constant Pi (π), which represents the ratio of a circle's circumference to its diameter. In this context, however, there is nothing particularly special about Pi, since the majority of irrational numbers - indeed the majority of real numbers - are transcendental. For an example of an irrational number that is not transcendental, we need look no further than the square root of two (√2), which is an algebraic number because it satisfies the simple polynomial equation x2 - 2 = 0. In fact this equation has two roots, √2 and -√2, as you can see below from the graph of the polynomial equation's corresponding function.
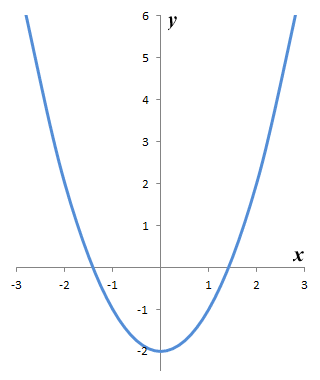
The graph of y = ƒ(x) = x2 - 2
German mathematician Georg Cantor (1845-1918) - one of the inventors of set theory (which we'll be looking at elsewhere in due course) was interested in the notion of infinity. However, he believed that there were different infinities - something we have already hinted at above. Cantor realised that the simplest infinity was that represented by the set of counting numbers. He rationalised that there must be an infinite number of counting numbers, because it doesn't matter how large a number is, we can always add one to that number and get another number. The counting numbers, therefore, must be countably infinite.
Cantor then came up with a way of determining if other sets of numbers were also countably infinite. In a nutshell, he stated that any set whose elements could be put into a one-to-one correspondence with the counting numbers must also be countably infinite. He further argued that some proper subsets of a countably infinite set were themselves infinite, and that sets that seemed like they must be considerably larger than the set of counting numbers were in fact the same size! Let's look at an example of a proper subset that is countably infinite first. Suppose we have the following function:
f(n) = 2n
where n = 1, 2, 3, . . .
This function, of course, produces the set of positive even numbers, so it would be natural to assume that the size of the resulting set would be only half that of the counting numbers. Cantor, however begged to differ. Consider the following sequence:
1 → 2
2 → 4
3 → 6
4 → 8
·
·
·
The function will produce a unique value for every counting number passed to it. There is thus a one-to-one correspondence between the numbers in the resulting set of even numbers and the counting numbers, hence the set of even numbers must also be countably infinite. For his next trick Cantor showed us that sets that we intuitively assume must be larger than the set of counting numbers are in fact the same size. He did this by pairing the counting numbers with the integers, as shown here:
1 → 0
2 → -1
3 → 1
4 → -2
5 → 2
6 → -3
7 → 3
·
·
·
For those of you unable to sleep, the one-to-one correspondence shown above is the output of the following function:
| f(n) = | n (-1) n(-1) | - | 1 - (-1) n |
| 2 | 4 |
where n = 1, 2, 3, . . .
Cantor was able to apply the same principle in order to prove that the set of rational numbers was not only countably infinite (which we kind of demonstrated above), but that it has the same size as the set of counting numbers. This last concept is somewhat hard to accept because, as we have already seen, rational numbers are pretty dense. By that we mean that, if you pick any two rational numbers you will be able to find another rational number between them. In fact, you'll be able to find an infinite number of rational numbers between them!
Nevertheless, it can be shown that every rational number can be paired with a different counting number in a one-to-one relationship. There are in fact several (somewhat convoluted) formulae that can be used to generate unique pairings between rational numbers and counting numbers, although a detailed explanation of how they work is beyond the scope of this article. The final point we want to cover here is how Cantor showed that the set of real numbers (ℝ) is uncountably infinite.
The method Cantor used to do this became known as the diagonal argument or diagonal method (it also has a few other names). Remember that for a set to be countably infinite, it must be possible to uniquely pair every member of that set with a member of the set of natural numbers. Cantor wanted to prove that this was not the case for the set of real numbers, so he began by assuming the opposite of what he wanted to prove, i.e. that every member of the set of real numbers could be uniquely paired with a member of the set of natural numbers.
Cantor's diagonal argument relies on a technique called proof by contradiction (also known as indirect proof). The technique is widely used in mathematics and science and goes way back to the days of the Greek philosopher and polymath Aristotle (384-322 BCE), who first formalised the law of noncontradiction, on which it is based, as a metaphysical principle. It establishes the validity of a proposition by showing that a denial of that proposition results in a contradiction.
Another way of saying that the set of real numbers (ℝ) is countably infinite is to say that we can list them. The assumption Cantor started with, therefore, is that ℝ is listable. In order to simplify the task somewhat, Cantor limited the scope of his investigation to the set of real numbers between zero and one. If those numbers cannot be put into a one-to-one relationship with the counting numbers, there is little point in taking things any further.
This number range contains at least one example of every kind of real number we have looked at so far, including whole numbers, rational numbers and irrational numbers. In order to list all of the real numbers in the range, however, we need to use a common form of representation for each number in the list. All of the numbers (except the last number, which is one) will thus represented as a zero, followed by an infinite string of digits. A partial list might look like this:
0.0000000000000000000000000000000 . . . .
0.2500000000000000000000000000000 . . . .
0.3333333333333333333333333333333 . . . .
0.4142135623730950488016887242097 . . . .
1.0000000000000000000000000000000 . . . .
Obviously attempting to construct an actual list of the real numbers, even assuming it to be possible, is not feasible. Cantor therefore came up with a symbolic list that took the following form:
x1 = 0.d1,1d1,2d1,3d1,4d1,5d1,6d1,7d1,8d1,9 . . . .
x2 = 0.d2,1d2,2d2,3d2,4d2,5d2,6d2,7d2,8d2,9 . . . .
x3 = 0.d3,1d3,2d3,3d3,4d3,5d3,6d3,7d3,8d3,9 . . . .
x4 = 0.d4,1d4,2d4,3d4,4d4,5d4,6d4,7d4,8d4,9 . . . .
x5 = 0.d5,1d5,2d5,3d5,4d5,5d5,6d5,7d5,8d5,9 . . . .
x6 = 0.d6,1d6,2d6,3d6,4d6,5d6,6d6,7d6,8d6,9 . . . .
·
·
·
xn = 0.dn,1dn,2dn,3dn,4dn,5dn,6dn,7dn,8dn,9 . . . .
In our list, x 1 is the first real number, x 2 is the second real number, and so on. Each real number is then written as zero, followed by the decimal point, followed by an infinite series of digits, each represented by the lower-case letter d followed by two subscripts. The first subscript in each case refers to the number's position in the list (i.e. x 1, x 2, x 3 etc.). The second subscript refers to the digit's position after the decimal point.
Now, given our initial assumption that the real numbers (in this case limited to the range zero to one) can be listed, i.e. that there is a one-to-one correspondence between those numbers and the counting numbers, it should not be possible to find a number that is not on our list. If we do find a real number that is not on the list, then we have found the contradiction, and our initial assumption - that the real numbers can be listed - must be wrong. It would also mean that the cardinality of the two sets - the real numbers and the counting numbers - cannot be the same.
So how do we come up with a new number to enable us to put this to the test? Cantor did it by taking the diagonal elements of the original list, i.e. d1,1, d2,2, d3,3, d4,4, d5,5, and so on, and adding one to each. Let's suppose we call our new number xnew. We can define it as:
xnew = 0.(d1,1+1) (d2,2+1) (d3,3+1) (d4,4+1) (d5,5+1) . . . . (dn,n+1)
Actually, things are not quite so straightforward as this, because each element must be a digit in the range 0 - 9, and adding 1 to 9 gives us 10. We actually take the modulo 10 value of the result of adding one to each element, so that if the result of adding one to an element gives us 10, it will become zero (the results for values of 0 - 8 are unchanged). For the sake of simplicity, however, we have omitted the modulo operation from our list.
We now have a new real number, xnew. If our initial assumption that ℝ can be listed and that there really is a one-to-one correspondence between the real numbers and the counting numbers, then we should be able to find xnew on our list. One way of doing that, of course, is to compare xnew with each number on the list in turn, until we find a match. Let's start by comparing xnew with x1. The numbers do not match because the first digit in x1 is d1,1, whereas the first digit in xnew is d1,1+1.
OK, so we move on to x2. This doesn't give us a match either, because the second digit in x2 is d2,2, while the second digit in xnew is d2,2+1. The same thing happens when we compare xnew with x3. The third digit in x3 is d3,3, while the third digit in xnew is d3,3+1. We could go on like this indefinitely, but the result will be the same. The real number xnew is not in our list. For any counting number n, xnew cannot be matched with xn in the original list because the original list has dn,n, but the new number has dn,n+1.
The conclusion must be that the real numbers cannot be put into a one-to-one correspondence with the counting numbers, and furthermore that the real numbers and the counting numbers do not have the same cardinality. A number of arguments have been put forward to challenge this conclusion, but so far none have proven successful. Cantor called it an uncountable infinity - there are simply too many real numbers to count. Other uncountable infinities include the number of points on a line, and the number of points on a plane.