| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The first derivative test is used to determine whether a specific critical point of a function is a local maximum, a local minimum, or neither of these things. Think about the values taken by a function immediately before and after a critical point. If these values are both less than the value of the function at the critical point, then the critical point is a local maximum. If they are both greater than the value of the function at the critical point, then the critical point must be a local minimum. If the value on one side of the critical point is higher and the value on the other side of the critical point is lower, then the critical point is neither a local maximum nor a local minimum. Consider the following illustration.
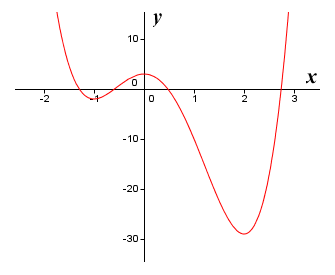
The graph of the function ƒ(x) = 3x 4 - 4x 3 - 12x 2 + 3
The illustration shows the graph of the polynomial function ƒ(x) = 3x 4 - 4x 3 - 12x 2 + 3. Because it is a polynomial function we know that it will be "well-behaved" in the sense that it will be both continuous and differentiable throughout its domain (this will not be the case with all of the functions we will encounter, but we'll cross that bridge when we come to it). Just by looking at the graph, we can see that there are local extrema at (or at least very close to) x values of minus one, zero and two. If you have read the section on Fermat's theorem, you will know that we can confirm the location of the function's (stationary) critical points by finding the roots of the first derivative function. Let's do that now. Applying the basic rules of differentiation, we get:
ƒ′(x) = 12x 3 - 12x 2 - 24x
Now we need to solve the equation:
12x 3 - 12x 2 - 24x = 0
We can immediately factor out 12x:
12x (x 2 - x - 2) = 0
The expression within the brackets will also factor quite nicely:
12x (x + 1)(x - 2) = 0
So x has three possible values - zero, minus one and two. This confirms what we assumed from inspecting the graph - that the x coordinates of the local extrema are zero, minus one and two. We can now apply the first derivative test to each of these points in turn to determine whether it is a local maximum, a local minimum or neither of these two things. But how does that work exactly?
Well, we know that, in order for a point to be a local maximum, the function must have a higher value at that point than at any other point on either side of it in its immediate vicinity - which is, after all, why we call it a local maximum. The function will be increasing in value as it approaches a local maximum from the left, and decreasing in value as it moves away from the local maximum to the right. This means that the slope of the function (i.e. the derivative) will be positive to the left of a local maximum and negative to the right of a local maximum. The exact opposite is true for a local minimum. In order for a point to be a local minimum, the function must have a lower value at that point than at any other point in its immediate vicinity The derivative will therefore be negative to the left of a local minimum and positive to the right of a local minimum.
We can state this a little more formally. Suppose we have a function ƒ(x) that is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), and that there exists a value c such that that a < c < b and (c, ƒ(c)) is a critical point of the function ƒ(x):
If ƒ′(x) > 0 to the left of (c, ƒ(c)) and ƒ′(x) < 0 to the right of (c, ƒ(c)), then (c, ƒ(c)) is a local maximum.
If ƒ′(x) < 0 to the left of (c, ƒ(c)) and ƒ′(x) > 0 to the right of (c, ƒ(c)), then (c, ƒ(c)) is a local minimum.
If ƒ′(x) has the same sign on both the left and the right of (c, ƒ(c)), then (c, ƒ(c)) is neither a local maximum nor a local minimum.
The illustration below shows the graph of the function ƒ(x) = 3x 4 - 4x 3 - 12x 2 + 3 once more, this time accompanied by the graph of the first derivative function ƒ′(x) = 12x 3 - 12x 2 - 24x. You should be able to see that the points at which the graph of ƒ′(x) intersects the x axis correspond to the x coordinates of the critical points of ƒ(x). We can use these points to divide the x axis into four separate regions, as shown.
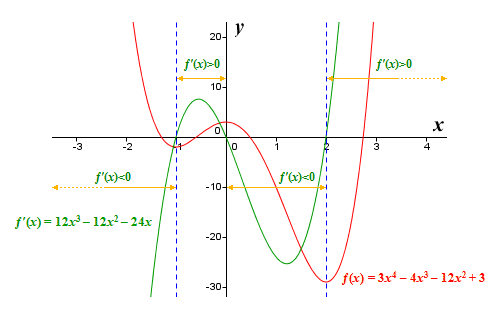
The graphs of the functions ƒ(x) = 3x 4 - 4x 3 - 12x 2 + 3 and ƒ′(x) = 12x 3 - 12x 2 - 24x
Since the function ƒ(x) = 3x 4 - 4x 3 - 12x 2 + 3 is a polynomial function and is therefore "well behaved", we know that the solving the derivative for x will yield all of the function's critical points. Thus, in the region to the left of x = -1, the value of ƒ′(x) will be increasingly negative as x itself becomes increasingly negative. Similarly, in the region to the right of x = 2, the value of ƒ′(x) will continue to grow as x increases. We can see that, for the region that lies between x = -1 and x = 0, the value of ƒ′(x) is positive. We can also see that, for the region that lies between x = 0 and x = 2, the value of ƒ′(x) is negative. Armed with this information, we can apply the first derivative test to classify the function's critical points.
For the critical point at x = -1, we have ƒ′(x) < 0 to the left of the point and ƒ′(x) > 0 to the right, so (-1, ƒ(-1)) is a local minimum.
For the critical point at x = 0, we have ƒ′(x) > 0 to the left of the point and ƒ′(x) < 0 to the right, so (0, ƒ(0)) is a local maximum.
For the critical point at x = 2, we have ƒ′(x) < 0 to the left of the point and ƒ′(x) > 0 to the right, so (2, ƒ(2)) is a local minimum.
Note that the last critical point in the list, (2, ƒ(2)), is also a global minimum for the function. Keep in mind, however, that the first derivative test can only be used to identify critical points as local extrema. It cannot be used to identify global extrema. The techniques used for this purpose will be examined elsewhere.
Before we move on, we should perhaps clarify one or two things. First, although the end point of an interval (assuming one has been defined) can be a global extremum (i.e. a global maximum or minimum), it cannot be a local extremum. Even if the endpoint of a function is found to be a global extremum, it cannot at the same time be a local extremum because the definition of a local extremum requires that there must be an open interval that contains the extremum, but this cannot be the case if the point in question is an endpoint.
Something else that will probably have occurred to you from studying the example shown above is that, once we have identified the critical points of the function, it is a simple matter to determine which of these points is a local maximum and which is a local minimum just by looking at the graphs of the function and its derivative. From the perspective of carrying out mathematical analysis, however, we need to be able to plug specific values of x into the first derivative function in order to determine its sign at a specific point. Suppose, for example, that we wanted to write a computer program to perform this kind of analysis. We would need to use a strictly algorithmic approach, because a computer cannot "see" where a point lies in relation to the x and y axes. It can only make that determination by analysing numerical data.
So far we have only looked applying the first derivative test to a polynomial function, which by definition will be both continuous and differentiable over its entire domain. We will turn our attention now to functions that are not so nicely behaved, to get an idea of what we can and cannot do with the first derivative test. First of all we should state that, in order to apply the first derivative test to a particular point, the function does not have to be differentiable at the point, but it must be continuous. The function must also be differentiable immediately to either side of the point. The following illustration shows the graph of the function ƒ(x) = |x| + 1.
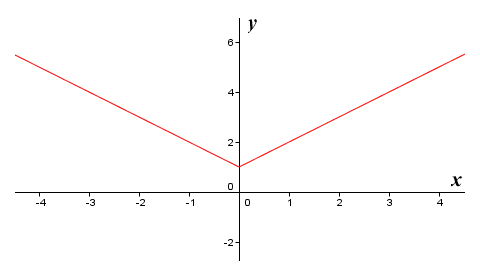
The graph of the function ƒ(x) = |x| + 1
The function ƒ(x) = |x| + 1 has a critical point at x = 0 which is not differentiable. The function is continuous at x = 0 however, and is also differentiable on either side of x = 0. You may be wondering how we arrive at this conclusion. Well, the derivative of the function can be written as follows:
| d | (|x| + 1) = | x |
| dx | |x| |
The derivative is therefore minus one (-1) for all values of x less than zero, and one (1) for all values of x greater than zero. When x is zero, the derivative does not exist (division by zero), even though the function itself does return a value (one). The function is therefore continuous at zero, and differentiable on either side of zero, so we can use the first derivative test at x = 0 to determine that (0, ƒ(0)) is a local minimum. Here is the graph of the function ƒ(x) = |x| + 1 once more, this time together with the graph of its derivative function (shown here in green):
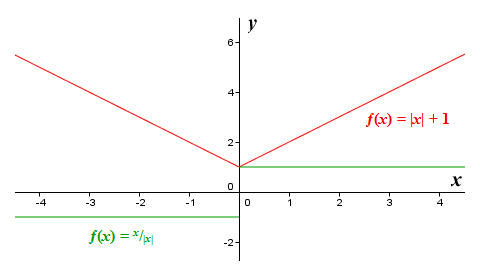
The graphs of the functions ƒ(x) = |x| + 1 and ƒ(x) = x/|x|
Clearly, the derivative ƒ′(x) is negative to the left of x = 0 and positive to the right of x = 0. The point (0, ƒ(0)) therefore satisfies the criteria for a local minimum, since the function ƒ(x) = |x| + 1 is both continuous at this point and differentiable immediately to either side of it. Let's look at another example. Here is the graph of the function ƒ(x) = 3√x, together with that of its derivative ƒ′(x) = 1/(3x 2/3) (shown in green). Note that at x = 0, the function is continuous because it has a value at this point (zero), but the derivative does not exist at x = 0. It does exist immediately to either side of the point x = 0, however, which means that we can use the first derivative rule.
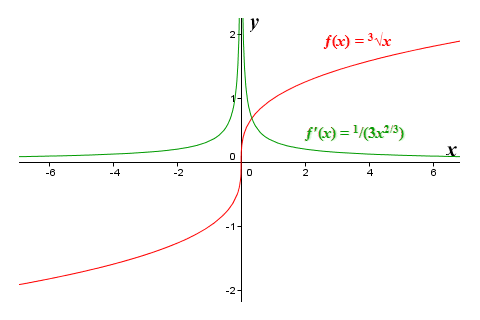
The graph of the function ƒ(x) = 3√x and its derivative ƒ′(x) = 1/(3x 2/3)
Since ƒ′(x) has the same sign on both the left and the right of (0, ƒ(0)), then according to the first derivative test, (0, ƒ(0)) is neither a local maximum nor a local minimum, but an inflection point (in fact, the function ƒ(x) = 3√x has no extrema within its domain of any kind whatsoever). This example and the previous example demonstrate that we will often encounter critical points to which the first derivative test can be applied, even if the derivative does not exist at these points. Some of them will be local extrema, others will be inflection points.
A reminder might be in order here of exactly what we mean by continuity. In simple terms, it means that we can draw the graph by hand without lifting the pencil from the paper. We obviously could not do that if there were some kind of discontinuity, i.e. a point where the curve has a gap or a sudden break in it. It does not necessarily imply that the function is not defined for every value of x (although that could indeed be the case). An example should serve to illustrate the point. Consider the following piecewise-defined function:
| ƒ(x) = | { | x 5 + 3.5x 4 - 3x 3 - 13x 2 + x + 3 for x < -1 |
| x 5 + 3.5x 4 - 3x 3 - 13x 2 + x - 3 for x ≥ -1 |
Here is the graph of the function:
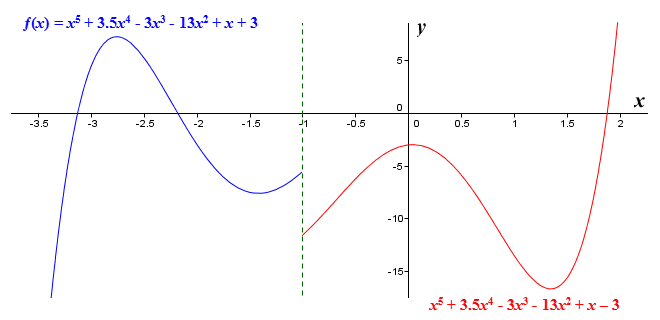
The graph of x 5 + 3.5x 4 - 3x 3 - 13x 2 + x + 3 for x < -1, x 5 + 3.5x 4 - 3x 3 - 13x 2 + x - 3 for x ≥ -1
You can see here that the function has a value for all values of x, but it is not continuous - we cannot draw the graph of the function by hand without taking the pencil off the paper. We have already said that if this is the case, we cannot apply the first derivative test. But what would actually happen if we attempted to do so? Let's have a look at our piecewise-defined function once more, this time together with its derivative. We will find all of the function's critical points, and apply the first derivative test to them.
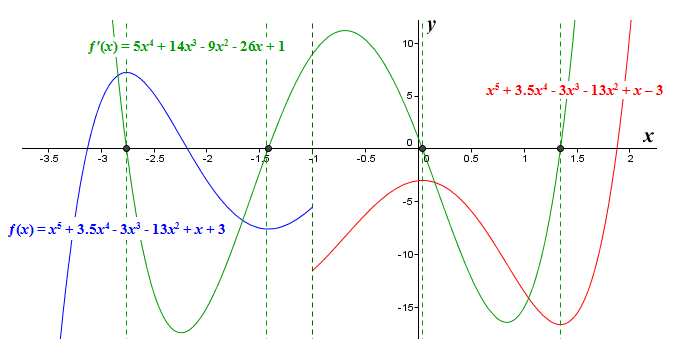
The first derivative test fails if the function has a discontinuity
You can see from the above that the derivative of our piecewise-defined function (shown in green) is the same for both parts of the function - namely the function ƒ′(x) = 5x 4 + 14x 3 - 9x 2 - 26x + 1. This is because the only difference between the two parts is the constant term, which of course disappears when we differentiate them. The derivative function cannot be factored, and has no rational roots that can be found using the rational root test. The roots must instead be found using quartic formulas. The roots (from left to right) are -2.76004, -1.42058, 0.03799, and 1.34263. Applying the first derivative test to find local extrema gives us the following results:
x = -2.76004 local maximum (ƒ′(x) changes from positive to negative)
x = -1.42058 local minimum (ƒ′(x) changes from negative to positive)
x = 0.03799 local maximum (ƒ′(x) changes from positive to negative)
x = 1.34263 local minimum (ƒ′(x) changes from negative to positive)
We also have a somewhat ambiguous situation at x = -1. The point (-1, ƒ(-1)) is a local minimum by virtue of the fact that it has the least value of any point in its immediate vicinity, and yet the point immediately to the left of (-1, ƒ(-1)) is a local maximum because it has the greatest value of any point in its immediate vicinity. Both points fall within an open interval, and ƒ(x) is defined for all values of x within that interval, so both points satisfy the definition of a local extremum. And yet, if we look at what the derivative is doing here, we see that to both left and right of both of these points the derivative is positive. If we were to apply the first derivative test to this situation, we would conclude that neither of these points is a local extremum, and yet we can see quite clearly that they are in fact both local extrema. This demonstrates what we stated earlier, which is that the first derivative test can't be meaningfully applied to a function at any point where a discontinuity occurs. If we try to do so, the test fails.
We mentioned earlier that an algorithmic approach can be developed that allows us to apply the first derivative test to some function to find local extrema without having to rely on being able to produce graphs of the function and its derivative. We will now outline that approach, and apply it to a simple example. Let's suppose we want to find all local minima and maxima for the function ƒ(x) = 3x 3 - 12x 2 + 7, defined on the interval [-1, 4]. We will solve this problem as follows:
ƒ′(x) = 9x 2 - 24x
9x 2 - 24x = 0
3x (3x - 8) = 0
x = 0 or x = 2.667

A number line with the x coordinates of interval boundaries and critical points
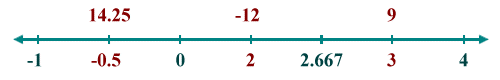
Add the intermediate points to the number line
If we apply the first derivative test as described here to the function ƒ(x) = 3x 3 - 12x 2 + 7, we will find that (0, ƒ(0)) is a local maximum, since the derivative is positive to the immediate left of (0, ƒ(0)) and negative to the immediate right. We will also find that (2.667, ƒ(2.667)) is a local minimum, because the derivative is negative to the immediate left of (2.667, ƒ(2.667)) and positive to the immediate right (note that, if we want to know the actual values of the two local extrema, we can simply plug their x coordinates into the original function). For completeness, here are the graphs of the function ƒ(x) = 3x 3 - 12x 2 + 7 and its derivative ƒ′(x) = 9x 2 - 24x.
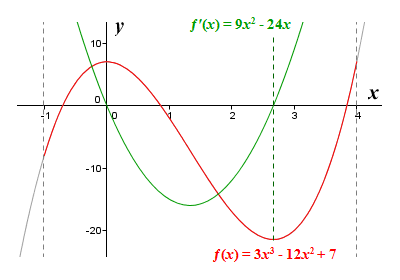
The graphs of ƒ(x) = 3x 3 - 12x 2 + 7 and ƒ′(x) = 9x 2 - 24x
The algorithm described above works for all polynomial functions, but would need some adjustment to be able to deal correctly with functions that are not "well behaved" in the sense that the domain of the function (or the interval in which we are interested) contains a discontinuity or some other kind of anomaly.