| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The cone is a three-dimensional object, somewhat similar in shape to a pyramid. In fact, you could visualize the cone as a pyramid that has an infinite number of sides (or to put it another way, a pyramid with a circular base). However, the cone is not a polyhedron, simply because it does have a circular base. It has single vertex (the apex of the cone) that lies at some distance from the base, and in a different plane. Whereas a pyramid has a finite number of triangular sides, each one connecting one side of the base polygon to the apex of the pyramid, a cone has a single, smoothly curved and tapered lateral surface that connects the circular base of the cone to its apex. The illustration below shows a square pyramid and a typical cone with similar proportions.
A square pyramid and a cone
The term cone, when not otherwise qualified, is usually assumed to refer to a right circular cone. A right circular cone is a cone that has a circular base, and an apex that is directly above the centre of the base. A circular cone for which the apex is not directly above the centre of the base is called an oblique circular cone, and a cone for which the base is an ellipse is called an elliptical cone. In this page, we are only going to concern ourselves with circular cones.
The lateral surface of the cone (i.e. the surface area of the cone excluding the base) can be thought of as all of the line segments connecting the apex to the base. From the illustration below you can see that, for a right circular cone, all of these line segments will be of the same length. In an oblique circular cone, the length will vary. For this reason, whereas we can use the same formula for finding the volume of an oblique circular cone as for a right circular cone, the formula used for finding the surface area of a right circular cone will not work for an oblique circular cone. In fact, there is no simple formula for finding the surface area of an oblique cone, and a discussion of how this might be achieved is beyond the scope of this page.
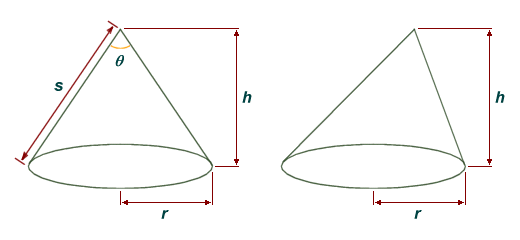
A right circular cone (left) and an oblique circular cone (right)
In the above diagram, for both the right circular cone and the oblique circular cone, r is the radius of the base, and h is the vertical height of the cone. For the right circular cone, s is the slant height of the cone (i.e. the distance between the apex of the cone and the perimeter of the base of the cone), and θ represents the aperture of the cone (i.e. the maximum angle that may exist between two line segments connecting the base of the cone to its apex). The formula for finding the volume of a circular cone (right or oblique) is pretty much the same as the formula for finding the volume of a pyramid. The volume V will be the product of the area of the base B and the vertical height (or altitude) of the cone h, multiplied by one third (1/3). We can express this formally as:
| V = | 1 | Bh |
| 3 |
Note that this is the same formula as that used to find the volume of a pyramid. However, since the base of the cone is a circle, and since the area of a circle is given as πr 2, where r is the radius of the circle, we can modify the formula to reflect this as follows:
| V = | 1 | πr 2h |
| 3 |
The total surface area A of a right circular cone is the area of the base plus the lateral area of the cone. The lateral area of a right circular cone is the product of its slant height s, the radius r of the base, and pi (π). We can express this formally as:
Lateral area = πrs
Thus the formula for the total surface area A of a right circular cone is:
A = πr 2 + πrs = πr (s + r)
Incidentally, if you are not given the slant height s of the cone, but know its vertical height h and the radius r of its base, you can calculate the slant height relatively easily. Given that s is the hypotenuse of a right-angled triangle for which r is the horizontal leg and h is the vertical leg, we can use Pythagoras' theorem to calculate the length of s as follows:
s = √(r 2 + h 2)