| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Cubes, cuboids and parallelepipeds are closely related three-dimensional polyhedra (a polyhedron is any three-dimensional shape that has straight edges and flat faces). You can probably think of the parallelepipeds as a family of shapes to which cuboids belong. Not all parallelepipeds are cuboids, but all cuboids are parallelepipeds. Similarly, cubes are a subset of the cuboid family and, although all cubes are cuboids (and hence also parallelepipeds), not all cuboids are cubes. Parallelepipeds and cuboids are discussed elsewhere. This page is concerned with what is probably the simplest three-dimensional object from a mathematical point of view, the cube.
As we have already established, the cube is a three dimensional shape with straight edges and flat faces, or polyhedron. Furthermore, the cube is a regular polyhedron (i.e. one for which all faces are regular, congruent polygons that are arranged in exactly the same manner around each vertex). The cube has six (6) faces, all of which are squares of the same size, and twelve (12) edges, all of the same length. The dihedral angle between all intersecting faces is ninety degrees (90°). Each of the cube's eight (8) vertices is formed by the junction of three of its faces. The cube can also be called a regular hexahedron (a hexahedron is any three-dimensional shape with six faces), and is one of the five platonic solids (a platonic solid is a regular convex polyhedron with all faces being regular congruent polygons, and the same number of faces meeting at each vertex).
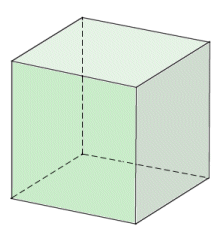
The cube is a regular polyhedron with six faces
There are other things we could say about cubes, but we have probably mentioned the most important features. It might seem, then, that this apparently simple geometric shape is perhaps more complex than we originally thought. It is however its very simplicity that allows it to belong to so many different classes of three-dimensional object at the same time. Cubes are found in various situations in our everyday lives. From childhood onwards we come across them, whether as children's building blocks, sugar lumps, ice cubes, and the dice used to play various games. Contrary to what you might think, cubes can also occur in nature. The image below shows naturally occurring iron pyrite crystals (iron pyrite, sometimes called fool's gold, is a compound formed from the elements iron and sulphur).

Iron pyrite crystals often form as cubes
A hollow cube can be flattened out in various ways (eleven different ways, to be exact) by cutting along some of its edges. The flattened version of a three-dimensional geometric shape is called a net. You may have come across nets of cubes in school. They are often used to construct a model of a cube from paper or card, when children are learning about geometric shapes. In order to create a net from a cube, we need to cut along seven (7) of its edges. The eleven possible permutations are illustrated below (note that if you come across a permutation that is apparently not the same as one of those shown below, you will find that it is either a reflected or a rotated version of one of them). Incidentally, if you want to make a model of a cube from card or paper, and then colour its faces so that no two adjacent faces are the same colour, you will need a minimum of three colours.
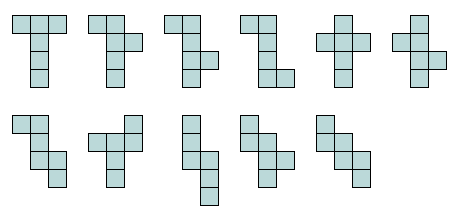
A cube can be flattened into 11 different nets
Interestingly, the cube is the only one of the five Platonic solids whose faces have an even number of sides, which also makes it a zonohedron. A zonohedron is a shape for which every face has point symmetry. That means that looking towards the central point of a face from two opposite directions, whatever those directions happen to be, you will always see exactly the same thing. As always with geometrical shapes, we are primarily interested in things like surface areas, volumes and the like. With that in mind, the most important formulae relating to the characteristics of a cube for which the length of each edge is a are given in the following table:
| Characteristic | Formula |
|---|---|
| Surface area: | = 6a2 |
| Volume: | = a3 |
| Face diagonal: | = a√2 |
| Space diagonal: | = a√3 |
| Radius of inscribed sphere: | = a ÷ 2 |
| Radius of circumscribed sphere: | = a√3 ÷ 2 |
| Radius of sphere tangent to edges: | = a ÷ √2 |
The first two formulae require little explanation. The surface area of a cube is simply the sum of the surface areas of its six faces, each of which are squares with a side length of a. The total surface area will thus be a2 multiplied by six. The volume of the cube is simply the area of one face of the cube (a2) multiplied by a, which gives us a3. As we mentioned earlier, the cube is also a cuboid. It is also probably worth mentioning here that a cube has the largest volume of any cuboid with a given surface area, and the largest volume of any cuboid having the same total linear size (length plus width plus height). The face diagonal is the line segment connecting opposite corners of any face of the cube, as shown below. It forms the hypotenuse of a right-angled triangle in which each leg is formed by one edge of the cube. Its length is thus √(2a2) = a√2.
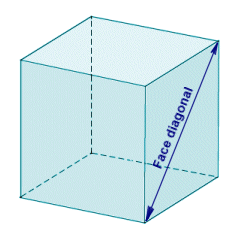
The face diagonal connects opposite corners of a face
The space diagonal is the line segment connecting opposite corners of any two opposite faces of the cube, as shown below. It forms the hypotenuse of a right-angled triangle in which one leg is a face diagonal and the other leg is one edge of the cube. Its length is thus √(a2 + 2a2) = √(3a2) = a√3.
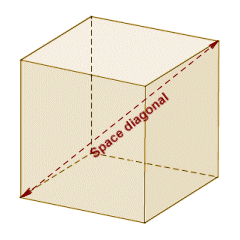
The space diagonal connects opposite corners of opposite faces
The last three formulae describe the relationship between a cube and various related spheres. A sphere that is totally contained within the cube, but that touches each face of the cube at a single point, is called an inscribed sphere. An inscribed sphere is illustrated below. Since both the cube and the sphere are symmetrical, it is reasonable to infer that the diameter of the sphere is the distance between any two opposite faces of the cube, i.e. a. The radius of the inscribed sphere is thus a divided by two.
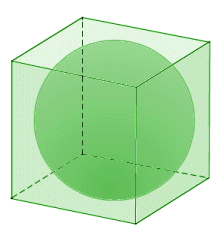
The inscribed sphere touches each face of the cube at a single point
A sphere that completely contains a cube, but that touches each of the eight corners of the cube at a single point, is called a circumscribed sphere. A circumscribed sphere is illustrated below. Again, since both the cube and the sphere are symmetrical, it is reasonable to infer that the diameter of the sphere is the distance between any two opposite corners of any two opposite faces of the cube, i.e. the diameter will have the same length as a space diagonal, which is given by a√3. The radius of the circumscribed sphere is thus a√3 divided by two.
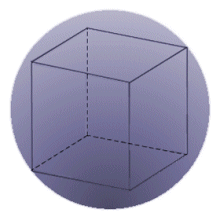
The circumscribed sphere touches each corner of the cube at a single point
The third kind of sphere of interest to us here is the sphere that is tangent to all of the cube's edges. Once more, given the symmetry of these shapes it is reasonable to assume that the sphere touches each edge at its mid-point, and that the diameter of the sphere will be the distance between opposite edges of opposite faces. The diameter will therefore have the same length as a face diagonal, which is given by a√2. The radius of the sphere that is tangent to all of the cube's edges is thus a√2 divided by two, which can be simplified to a divided by √2. Note that the sphere does not totally enclose the cube. Neither does the cube totally enclose the sphere.
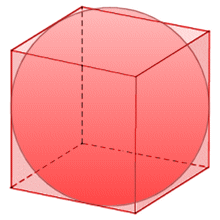
The sphere tangent to the edges of the cube touches each edge at a single point