| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The secant function is a trigonometric function, one of three reciprocal functions that we look at in these pages, the other two being the cosecant function and the cotangent function. A reciprocal function is one that is the reciprocal (or multiplicative inverse) of another function (see below). The secant function (usually abbreviated as sec) is the reciprocal function of the cosine function. As with the other trigonometric functions in modern use, the secant function was certainly known to Arab scholars, and tables of secant values are known to have been in existence by the tenth century CE. In order to clarify exactly how the secant function and the cosine function are related, consider the diagram below.
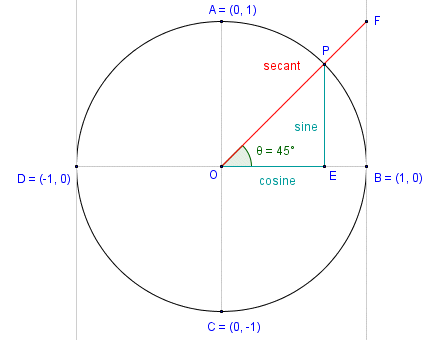
The secant as a line segment of the unit circle
Like the other trigonometric functions, the secant can be represented as a line segment associated with the unit circle. The diagram shows the secant for an angle of rotation θ of forty-five degrees (measured anti-clockwise from the positive x-axis). Line segment BF lies on the line that is tangent to the circle at point B. Line segment OF (shown in red) represents the secant, and is an extension of line segment OP. Remember that point P is a point on the circumference of the circle whose x and y coordinates represent the value of cos (θ ) and sin (θ ) respectively (the line segments representing the sine and cosine are also shown). Click here to see an interactive demonstration that uses the unit circle to show how the cosine and the secant functions relate to one another (note: your browser must support Java in order for the interactive page to work).
If you haven't already deduced the fact from the diagram, you will see from the interactive demo that as the value of cos (θ ) approaches one, so does the value of sec (θ ). As the value of cos (θ ) approaches zero, however, the value of sec (θ ) tends to infinity. The value of sec (θ ) when cos (θ ) equals zero is thus said to be undefined. Obviously, since the secant function is the reciprocal of the cosine function, it can be expressed in terms of the cosine function as:
| sec (θ ) = | 1 |
| cos(θ ) |
Since the cosine is represented by the x coordinate of point P (i.e. the point at which the terminal side of angle θ intersects the circumference of the circle), we can also conclude that:
| sec (θ ) = | 1 |
| x |
We can also define the secant in terms of a right-angled triangle. If you have read the pages in this section covering the three main trigonometric functions (sine, cosine and tangent) you will by now be familiar with the diagram below.
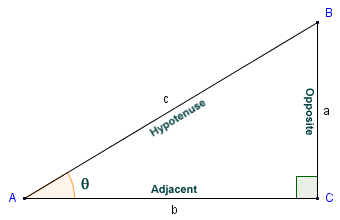
In triangle ABC, sec (θ ) = c/b
In right-angled triangle ABC, the cosine of angle θ is the quotient of the adjacent and the hypotenuse (i.e. the sides labelled b and c respectively). Since the secant function is the reciprocal of the cosine function, then the secant of angle θ will be the quotient of the hypotenuse and the adjacent. This gives us:
| sec (θ ) = | 1 | = | hypotenuse | = | c |
| cos(θ ) | adjacent | b |
For those interested in such things, we have used Microsoft Excel to produce our own table of secant values for angles ranging from zero degrees (0°) up to three hundred and sixty degrees (360°) in increments of one tenth of a degree. To see the table, click here.
If you study the table, you can see that there is a significant range of angles centred around zero degrees (0°), one hundred and eighty degrees (180°) and three hundred and sixty degrees (360°) for which the value returned by the secant function is quite small and changes relatively slowly. For angles close to either ninety degrees (90°) or two hundred and seventy degrees (270°) however, the value returned by the secant function rapidly gets bigger. This is to be expected, since the value of cos (θ ) will be very small for these angles, so its reciprocal will be correspondingly large. In fact, the value returned by the secant function for an angle of either ninety degrees or two hundred and seventy degrees is considered to be undefined, since the equation sec (θ ) = 1/cos (θ ) will involve division by zero. In fact, it will apply to any angle for which the cosine value is zero. We present below the graph of the secant function for angles in the range zero to seven hundred and twenty degrees (720°).
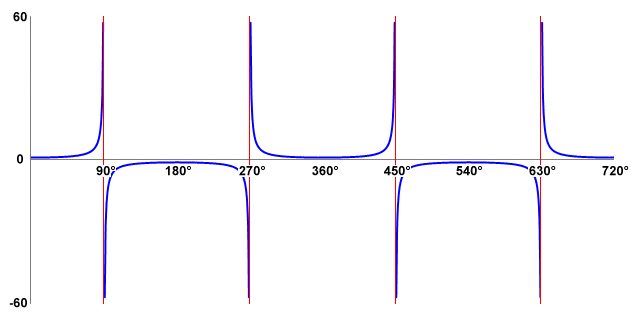
A graph of the secant function for angles in the range 0° to 720°
Because the absolute value of the cosine of an angle will never exceed one, the reciprocal of the cosine of an angle will never be less than one. So, just as the secant value is undefined for any angle for which the cosine is zero, it will always be one for any angle for which the cosine is one, and minus one for any angle for which the cosine is minus one. In fact, as you can see from both the tables and the graph of the secant function, the secant value is negative for all angles for which the cosine is negative. Like the graph of the tangent function, the graph of the secant function can include some very large positive and negative peaks, as the value of cos (θ ) tends to zero. Unlike the tangent function however, the period of the secant function is three hundred and sixty degrees (360°), or 2π. Like the cosine function, the secant function returns positive values for angles in Quadrants I and IV, and negative values for angles in Quadrants II and III.
If you have read the pages on tangents and cosecants (or possibly even if you haven't) you will know that the vertical red lines on the graph are asymptotes. The asymptote of a curve is a line such that as the distance between the curve and the line approaches zero, the value of the curve approaches infinity. In this case, the asymptotes can be considered to be the "gaps" in the graph where the value of sec (θ ) is undefined. Notice also that as the graph crosses the asymptote, the value of sec (θ ) transitions from its maximum positive value to its maximum negative value (or vice versa). You can also see how the values differ on either side of the asymptote by studying the table of secant values.
As with the other trigonometric functions we have looked at, we don't need to use tables to find the secant of an angle (or the angle corresponding to a given secant value), since any modern scientific calculator can do it for us, even though most calculators don't have a dedicated button for the secant function. Finding the secant of an angle with the built-in calculator provided in Microsoft Windows is still relatively straightforward. Let's assume we want to find the secant of an angle of twenty-five degrees (25°). You can find the Microsoft Windows built-in calculator by clicking on the start button in Windows 7 and selecting All Programs>Accessories>Calculator (other versions of Windows might require a different sequence of keystrokes). The scientific version of the calculator can be selected from the application's View menu. To find the secant of twenty-five degrees using the Windows calculator, enter the following keystrokes (if you don't have the Windows calculator, use any available calculator that can perform trig functions):
Enter these keystrokes to find the secant of 25°
Since the secant function is the reciprocal of the cosine function, all we have done here is to use the cosine function button on the calculator, and then apply the calculator's built-in reciprocal function button (usually labelled 1/x) to the result. Make sure, by the way, that you have the calculator set to the Degrees mode (unless you are planning to enter a value for the angle in radians or gradians). If you have entered the keystrokes correctly, you should now see the following display:
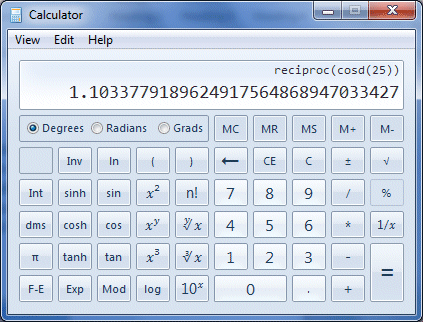
The calculator displays the value of sec (25°)
So far, so good. Now let's assume that you want to find the size of an acute angle in a right-angled triangle by first finding the quotient of the hypotenuse and adjacent (i.e. the angle's secant). Providing you have values for the lengths of the sides of the triangle, you can find the value of the angle's secant easily enough. Finding the angle is not quite as straightforward as for the three main trigonometric functions, as most calculators do not have a dedicated button for the arcsecant function (which is the inverse of the secant function). Fortunately, there is a relatively simple way around that. Let's find the value of angle θ for the right-angled triangle illustrated below.
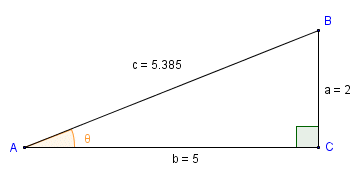
We want to find the size of angle θ
For angle θ, sides c and b are the hypotenuse and the adjacent respectively. We can actually find the size of the angle in a single operation on the Windows calculator. We do this by using brackets in the key sequence entered, in order to get the calculator to find the inverse of the quotient of the hypotenuse and adjacent (i.e. the secant of the angle) first. We then apply the arccosine function to the result. Here is the key sequence to use:
Enter these keystrokes to find the size of angle θ
You may have already worked out that what we did here was to find the cosine of the angle by taking the reciprocal of the secant. We then simply applied the arccosine function to the result. If you have entered the keystrokes correctly, you should now see a display like the one shown below. If you have read the page entitled "The Cosecant Function" you will by now realise that all of the trigonometric functions are very closely interrelated. No real surprise then, that the similarity between the graphs of the sine and cosine is mirrored by the similarity between the graphs of the cosecant and secant, with the only real difference in both cases being a ninety degree phase difference. The fact that the trigonometric functions are so closely interrelated means that we can often replace an expression involving one trigonometric function with an equivalent expression involving a different trigonometric function. This can often be very useful.
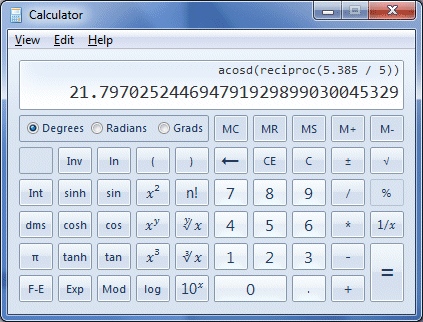
The calculator displays the value of angle θ
The secant function, in common with other trigonometric functions, can be represented as an infinite series. The value returned by a trigonometric function for a given angle cannot be calculated using a simple algebraic formula. For most angles, an exact value can only be obtained as the sum of an infinite number of terms, which is obviously impossible to achieve. A reasonably accurate approximation of the value is found using the sum of a limited number of terms from the function's infinite series. The greater the number of terms included, the greater the accuracy of the result. The number of terms used will depend on the accuracy required, and on the computational resources available. The infinite series frequently cited for the secant function looks like this:
| sec (x) = 1 + | 1 | x2 + | 5 | x4 + | 61 | x6 + | 277 | x8 + · · · · |
| 2 | 24 | 720 | 8064 |