| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The dot product of two vectors is always a scalar value. For that reason, it is sometimes called the scalar product. The scalar value produced is closely related to the cosine of the angle between the two vectors, i.e. the angle produced by placing them tail to tail, as shown below. The cosine function is a trigonometric function, and while you don't need an in-depth understanding of trigonometry to understand the material on this page, you do need to know how to use the cosine and arccosine buttons on your calculator correctly. The dot product of two vectors is relatively easy to find. We just need to know the x and y components for each vector. We'll start by finding the dot product of two vectors, a and b.
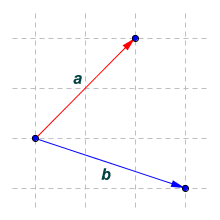
We want to find the dot product for vectors a and b
The dot product of the vectors is expressed as a · b. The use of the middle dot ("·") symbol here is somewhat unusual, since it is normally used to signify multiplication between two scalar values. In this case, we are multiplying together the components of the two vectors, i.e. the two x components are multiplied together, and the two y components are multiplied together. The results of these multiplication operations are then added together to get the dot product. Finding the dot product is straightforward if you know the x and y components of the two vectors (note that we can also find the dot product of three-dimensional vectors - we just need to include the product of the z components). The dot product for vectors a and b is found as follows:
a · b = axbx + ayby = ((2)(3)) + ((2)(-1)) = 6 - 2 = 4
We can use another method of finding the dot product if we know the magnitude (i.e. the length) of each vector, and the angle θ between the two vectors. This is the part, by the way, where you need to use the cosine button on your calculator. The illustration below shows the two vectors a and b once more. This time, the magnitude of each vector and the angle between them are also shown.
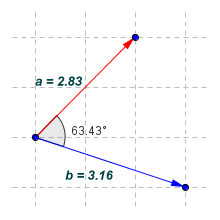
We now know the magnitude of each vector and the angle between them
Here is the equation for finding the dot product of vectors a and b using the cosine function. Note that the magnitude of a vector is signified by placing the vector name between two vertical bars.
a · b = |a||b| cos (θ )
Substituting actual values, we get:
a · b = 2.83 × 3.16 × 0.447 = 4.0
This is the same answer we had previously, which is as we would expect. Note that if we are not given the vector lengths, we can always find them using Pythagoras' theorem so long as we know the x and y components of each vector. You may be asking yourself at this point why, if we know the x and y components anyway, would we not simply use them to find the dot product as we did before. If all we wanted was to find the dot product, it might be easiest to do just that. On the other hand, for many of the problems we come across (in engineering or the study of physics, for example), the magnitude of the vectors and the angle between them are known quantities, in which case it is probably easier to use the cosine equation.
Being able to find the dot product of two vectors is useful in a number of situations. It allows us, for example, to calculate the amount of work carried out by some physical system. Imagine a tractor pulling a concrete block, as illustrated below. The tractor is pulling the block with a constant force so that it moves horizontally along the ground.
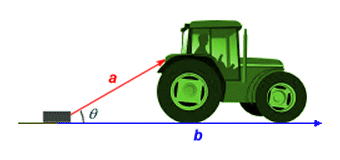
The tractor pulls a concrete block through distance |b|
Because vector a is pointing in a different direction from vector b, only some of the force applied by the tractor is acting in the direction in which the block is moving. The work done in moving the block is given as the distance moved (given by |b|) multiplied by the applied force, i.e. that component of the total force applied by the tractor (given by |a|) that is acting in the direction of motion (in other words, in the same direction as vector b). The actual work done is given by the dot product of vectors a and b.
Work done = a · b = |a||b| cos (θ)
If the tractor could pull the block horizontally, then all of the applied force would be acting in the direction of vector b. This could perhaps be achieved by placing a tow hook on the tractor at the same height as the attachment point on the block. Vector a would then act in the same direction as vector b, and angle θ would become zero degrees (giving a cosine value of one). The equation would reduce to:
Work done = a · b = |a||b| (force times distance)
It may be the case that we don't actually know the angle between vectors a and b, and need to find it. We can do this by rearranging our cosine equation as shown below (this is the part where you need to use the arccosine button (usually labeled cos-1) on your calculator. Whereas the cosine button returns the cosine value for a given angle, the arccosine button returns the angle that corresponds to a given cosine value). Here is the rearranged equation:
| θ = cos-1 | a · b |
| |a||b| |
Putting actual values into the equation, we get:
| θ = cos-1 | 4 | = cos-1 (0.447) = 63.43° |
| 2.83 × 3.16 |
If you try the calculation yourself, the answer you get may vary slightly from that shown due to rounding errors, but it should be sufficiently accurate for most purposes. Something to note here is that, if the vectors are perpendicular (i.e. at right-angles to one another), the value of cos (θ) will be zero. Vectors that are at right-angles to one another are said to be orthogonal. Sometimes the vectors are parallel to one another (i.e. acting in the same direction). In this case, angle θ will be zero degrees and the value of cos (θ) will be one.
As we saw above, when the tractor is pulling the block, the force is applied at an angle to the direction in which the block is being moved. Only some of the total force applied by the tractor is doing the work required to move the block. We often need to know what proportion of an applied force is being used to do carry out some task in a physical system, either so that we can increase the efficiency of the system, or to enable us to predict the behaviour of similar systems. In the case of our tractor, the force being applied in the direction of vector b will be some proportion of the force acting in the direction of vector a.
We can find out just how much of the total force applied by the tractor is used to pull the block using something called the scalar projection (sometimes called the vector projection). Probably the best way to explain how the scalar projection works is to look at an example. The illustration below shows vectors a and b once again. This time we have drawn the scalar projection of vector a onto vector b, for which we use the notation ab. As you can probably see from the diagram, we find the scalar projection ab by drawing a line segment from the tip of vector a to vector b such that the line segment is perpendicular to vector b. The scalar projection is the part of vector b that lies between its tail and the point where the line segment intercepts it.
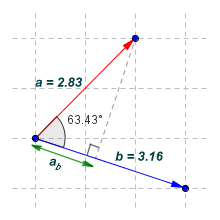
The scalar projection
We can use a further variation of the dot product cosine equation to tell us how much of one vector is projected onto another vector. The scalar projection of a onto b (i.e. the length of ab) is given by:
ab = |a| cos (θ )
and since
a · b = |a||b| cos (θ )
then
| ab = | a · b |
| |b| |
Substituting actual values, we get:
| ab = | 4 | = 1.266 |
| 3.16 |
From the above, it should now be clear that all we need to find the dot product of two vectors are the x and y components of the vectors. Alternatively, the dot product can be found if we know the magnitude (length) of the vectors and the angle between them. We just need to apply a little bit of trigonometry. The dot product is very useful in a number of situations, such as calculating the work done by a physical system, finding the distance between a point and a line, or finding the volume of a parallelepiped (for those that don't know, a parallelepiped is a polyhedron with six faces, each of which is a parallelogram!) In fact it crops up all over the place, so you would be well advised to become thoroughly familiar with it.