| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The term classical mechanics was first used early in the twentieth century to describe a branch of physics that was largely dominated by the physical laws formulated by the seventeenth century English physicist and philosopher Sir Isaac Newton (1642-1726). For that reason, classical mechanics is also often referred to as Newtonian mechanics.
As is invariably the case, Newton's work was based in no small measure on the work of his predecessors. In so far as the history of classical physics can be thought of as having a starting point, we probably need to go back to 1543 - almost one hundred and fifty years before Newton published his masterwork Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy).
In that year, the Polish astronomer Nicolaus Copernicus (1473-1543) published his book De revolutionibus orbium coelestium libri VI (Six Books Concerning the Revolutions of the Heavenly Orbs). Copernicus was already dying from the effects of a stroke at the time of publication, but allegedly regained consciousness on his deathbed just long enough to be presented with a printed copy of his great work, after which he promptly died.
Whilst this story is probably apocryphal, there can be no question as to the profound influence his work would have on the future of science. Copernicus had determined, not unreasonably, that the observed positions of the planets in the night sky would be much easier to explain if the Sun, rather than the Earth, were at the centre of the solar system.

The system of the entire created universe (Planisphere) according to the hypothesis of Copernicus exhibited in a planar view (illustrated in 1661 by Andreas Cellarius)
Unfortunately, not only did Copernicus' theories go against contemporary thinking, they raised a rather awkward question: If the Earth is careering through space, and at the same time spinning around its axis, why can we not detect this motion? The notion that the Earth was moving in such a fashion would have appeared nonsensical to a casual observer.
Copernicus died before he could offer anything in the way of proof to back up his ideas. Nevertheless, the events set in motion by Copernicus would become what is often referred to today as the scientific revolution. Finding an answer to the question that had now become so problematic for those who wished to pursue Copernicus' theories would fall to the Italian philosopher, astronomer and mathematician Galileo Galilei (1564-1642).
Galileo carried out numerous experiments to determine the nature of bodies in motion. In one experiment, he allowed a ball to roll down a slope, opposite which was a second slope. He noted with interest that the ball would roll up the second slope to almost the height from which it was released on the first slope; furthermore, the respective angles of the slopes seemed to have little bearing on the height attained by the upward-moving ball.
Galileo deduced from this experiment that if, instead of encountering the second slope, the ball found itself on a continuous level plane, it would continue to move in the horizontal direction indefinitely. He concluded that a body that is already in motion in the horizontal direction will continue to move in that direction unless something impedes its progress, and that no additional force needs to be applied to the body in order to maintain its momentum.
This conclusion was later refined by the French philosopher, mathematician, and scientist René Descartes (1596-1650), who determined that the concept applied specifically to motion in a straight line; this would later form the basis for Newton's first law - the law of inertia.
Galileo also experimented with falling bodies of different masses. He is famously alleged to have dropped two cannonballs, differing from one another in both size and mass, from the Leaning Tower of Pisa in order to demonstrate that they would both fall at the same rate regardless of their respective masses. Whether this experiment actually took place is the subject of some debate; nevertheless, Galileo correctly determined that a freely falling body will accelerate uniformly, at a rate that does not depend on its mass.
Galileo also correctly surmised that the motion of a projectile was subject to movement in two principle directions simultaneously; in addition to movement in the horizontal direction, the projectile was also moving in the downwards direction (a falling motion). He expressed this concept in his book Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla meccanica (or Dialogues Concerning Two New Sciences), in which he states:
It has been observed that missiles and projectiles describe a curved path of some sort; however no one has pointed out the fact that this path is a parabola. But this and other facts, not few in number or less worth knowing, I have succeeded in proving; and what I consider more important, there have been opened up to this vast and most excellent science, of which my work is merely the beginning, ways and means by which other minds more acute than mine will explore its remote corners.
Those prophetic words would later be borne out by the work of Newton. Perhaps of more immediate significance, however, was the fact that Galileo had found an answer to the problem arising from Copernicus' theories, namely the question of why an observer on Earth experiences no sensation of motion, despite the fact the Earth is supposedly moving through space at high speed and revolves around its axis.
One of the arguments frequently made against the notion that the Earth was moving went something like this: If the Earth is moving, then surely a stone dropped from a tower should move away from the tower as it falls? Galileo could now argue that, since the stone must be moving in the same direction as the tower immediately before it is dropped, then it will continue to move in that direction unless some external force or entity prevents it from doing so.
Galileo later became even more convinced of the veracity of the heliocentric view of the solar system when the invention of the telescope in (circa) 1610 allowed him to look more closely at the motion of various objects in the night sky. Galileo's observations led him to the discovery of Jupiter's four largest moons (which he at first thought were stars). After studying these objects for several weeks he concluded that they must be orbiting Jupiter just as, according to Copernicus, the planets of the solar system must orbit the Sun.

A painting by Henry-Julien Detouche showing Galileo Galilei displaying his telescope to Leonardo Donato
Nevertheless, there was still a great deal of hostility towards the heliocentric view of the solar system, not least because it directly contradicted the official view of the Catholic church at the time, which was that the Earth was at the centre of the universe, and that the Sun, Moon and stars revolved around it. Indeed, Galileo's support of heliocentrism put him on a collision course with the church that eventually led to him being tried for heresy, and saw him forced to spend the last few years of his life under house arrest.
The Copernican view of the solar system was also endorsed by the German mathematician, astronomer, and astrologer Johannes Kepler (1571-1630), who was to become one of the key figures in the scientific revolution. Kepler learned of the Copernican system of planetary motion as a student, and became a dedicated supporter of Copernicus' ideas. Kepler had proved himself to be an outstanding mathematician, and when his studies ended he accepted a post teaching mathematics in Graz (the second largest city in Austria).
During Kepler's tenure in Gratz, and based on his knowledge of three-dimensional geometry, he gradually developed a working theory concerning the geometrical ordering of the planets in the solar system. These ideas appeared in his first major astronomical work Mysterium Cosmographicum (The Cosmographic Mystery), which was originally published in 1596. A greatly expanded edition, which included a number of corrections and improvements, was published in In 1621.
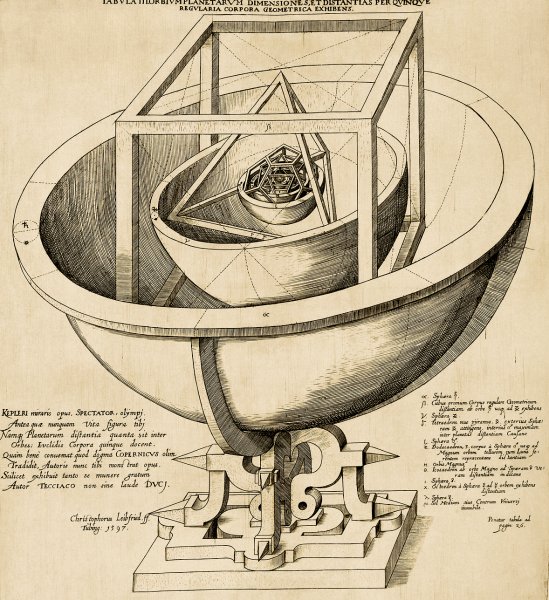
Copper engraving illustrating Johannes Kepler's Geometrical Model of the Copernican System, 1597
In pursuance of his theories, Kepler sought the opinions of many other astronomers of the period. He entered into a correspondence with the Danish nobleman and astronomer Tycho Brahe (1546-1601) - imperial mathematician to the Holy Roman Emperor (and King of Hungary) Rudolf II. Brahe was renowned for his accurate and comprehensive astronomical and planetary observations.
In 1600, Kepler met with Brahe in Prague. As a result of that meeting, he accepted a post as Brahe's assistant, and was assigned the task of analysing the observational data that Brahe provided. When Brahe died rather unexpectedly in 1601, Kepler succeeded him as imperial mathematician. His brief was to complete Brahe's unfinished work, and to provide astrological services to the Emperor.
Kepler remained in Prague until 1612, and spent those years analysing the extensive observational data that Brahe had gathered. It was in 1610, towards the end of his tenure there, that Galileo discovered the moons of Jupiter. Galileo sought the opinion of Kepler on this matter, who was happy to lend his support to Galileo's findings and later published his own observations of Jupiter's moons.
Kepler's work had a number of important outcomes. One of these was the Tabulae Rudolphinae (Rudolphine Tables) - a star catalogue and a set of planetary tables based on Brahe's observational data, named for the Emperor and eventually published by Kepler in 1627. In 1609, Kepler published his book Astronomia nova the full title of which (in English) is New Astronomy, Based upon Causes, or Celestial Physics, Treated by Means of Commentaries on the Motions of the Star Mars, from the Observations of Tycho Brahe, Gent.
The book contains the results of Kepler's investigation of the motion of Mars, from which he concluded that Mars follows an elliptical orbit around the Sun. The Astronomia nova is considered one of the most important books in the history of astronomy, and presents convincing evidence for heliocentrism. It was also the publication in which Keppler stated his first two laws of planetary motion, which can be summarised as follows:
Keppler's third law of planetary motion, along with the first two laws, would appear in the first volume of his textbook Epitome astronomiae Copernicanae (Epitome of Copernican Astronomy), published in seven parts between 1618 and 1621. The third law describes the relationship between the distance of a planet from the Sun and its orbital period; it states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
Kepler's textbook was to become perhaps his most influential work. In fact, during the twenty year period following Kepler's death in 1630, Epitome astronomiae Copernicanae was probably the most widely read astronomy text in Europe. Kepler's work went a long way towards legitimising Copernicus' notions of a heliocentric solar system. Although his rules concerning planetary orbits were widely accepted, however, there was far less enthusiasm for his ideas concerning the physical causes of these motions.
In 1665, thirty five years after Kepler's death, a twenty-three year old Isaac Newton returned from his studies at Trinity College Cambridge to his home in Woolsthorpe, Lincolnshire, the college having been temporarily closed down as a precaution against an outbreak of bubonic plague that was affecting Southern England, including parts of East Anglia, at that time. In Cambridge, Newton had been become familiar with the work of - among others - Descartes, Galileo and Kepler.
Although Newton would not publish his Principia until 1687, many of the ideas and theories for which he is so well known were developed over the next two years during his time at Woolsthorpe. During this period he developed the branch of mathematics we know today as calculus, did a considerable amount of work in the field of optics, and formulated his ideas on gravitation.
The credit for developing infinitesimal calculus is today generally acknowledged to belong jointly to Newton and the German polymath and philosopher Gottfried Wilhelm Leibniz (1646-1716), who independently developed his own version of the calculus during the same period. At the time, however, both Newton and Leibniz claimed to have developed the calculus first, leading to a bitter intellectual dispute that lasted many years and continued even after Leibniz's death in 1716.
The calculus was of critical importance because it provided the mathematical tools that made it possible to study phenomena in which the parameters undergo continuous change - in much the same way that geometry provides us with the tools to study two- and three-dimensional shapes, and algebra allows us to work with quantities whose value is unknown. Calculus is today used extensively in just about every branch of science.
It is often claimed that Newton's theories concerning gravity were inspired by an event that allegedly took place whilst he was sitting beneath an apple tree in his mother's garden in Woolsthorpe, in which an apple fell on his head. Newton himself never wrote of the incident, but the following account is given by the English antiquarian William Stukeley (1687-1765) in his biography of Newton "Memoirs of Sir Isaac Newton's Life":
"After dinner, the weather being warm, we went into the garden & drank thea under the shade of some appletrees, only he, & myself. Amidst other discourse, he told me, he was just in the same situation, as when formerly, the notion of gravitation came into his mind. 'Why should that apple always descend perpendicularly to the ground,' thought he to himself: occasion'd by the fall of an apple, as he sat in contemplative mood: 'Why should it not go sideways, or upwards? But constantly to the Earth's centre? Assuredly, the reason is, that the Earth draws it. There must be a drawing power in matter. & the sum of the drawing power in the matter of the Earth must be in the Earths centre, not in any side of the Earth. Therefore does this apple fall perpendicularly, or towards the centre. If matter thus draws matter, it must be proportion of its quantity. Therefore the apple draws the Earth, as well as the Earth draws the apple."

Newton's theory of gravitation is thought to have been inspired by an apple falling from a tree
The question that occupied Newton, who had a particular interest in the Moon and its orbit around the Earth, was not whether gravity existed, but whether its effects extended so far that it could be the force responsible for holding the Moon in its orbit. He finally came to the conclusion that the gravitational attraction between two bodies must extend over great distances, and that the strength of the gravitational attraction between two bodies was inversely proportional to the distance that separated them.
This conclusion was generally in agreement with Keppler's third law, which stated that the period of a planet's orbit was dependent only on its distance from the Sun. Newton was eventually able to show that gravity was responsible for the orbital motions of all of the planets in the solar system, prompting him to name it "universal gravitation".
By applying his theories regarding gravitational forces, Newton was able to derive Keppler's three laws of planetary motion mathematically, removing any lingering doubts about the validity of a heliocentric model of the solar system (although his inability to explain the physical nature of gravity led to accusations from some quarters that he was bringing "occult agencies" into science).
Newton's work laid the foundations of classical mechanics as we understand it today, and culminated in the publication, in 1687, of his master work, Philosophiæ Naturalis Principia Mathematica. In it Newton states his law of universal gravitation, and the three laws of motion which describe the relationship between an object, the forces acting upon it, and the object's resulting motion.
Newton's influence on the development of classical mechanics, and his contribution to science generally, make him one of the most important figures in the history of science. He nevertheless had the modesty to acknowledge the debt he owed to those upon whose work he built, including that of Galileo and Keppler. In a letter written in 1676 to fellow English scientist Robert Hooke (1635-1703), he famously wrote:
"If I have seen further it is by standing on the shoulders of giants."