Answers to Problems - RC Circuits

1. Consider the circuit shown below and think about what will happen after the switch is closed.
   
   
   
   
   
   
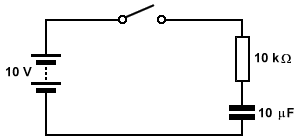
   a. What will be the maximum current through the resistor?
   
   

   The maximum flow of current through the resistor will occur at the instant the switch is closed, and will be:

   
   

   V	=	10 V	=  1 mA
   R		10 kΩ

   
   
   
   b. What will be the maximum charge on the capacitor?
   
   

   The maximum charge on the capacitor will be achieved when the potential difference across the capacitor is equal to the terminal voltage of the battery, and will be:

   
   

   Q  =  V  ×  C  =  10 V  ×  10 μF  =  100 μC

   
   
   
2. Examine the circuit shown below. Assume that the capacitor is initially uncharged, with the switch in the position shown on the diagram. The switch will be moved to position A for exactly 5 seconds, then to position B for exactly 5 seconds, then back to its original position.
   
   
   
   
   
   
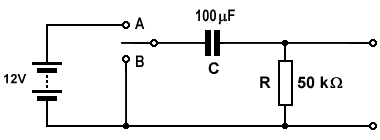
   What is the potential difference across capacitor C and the voltage drop across resistor R when:
   
   
   a. the switch has been in position A for 5 seconds?
   
   

   The time constant for the circuit is 100 μF × 50k Ω = 5 (seconds), therefore the capacitor voltage V_C is given by:

   
   

   V_C  =  0.63  ×  12 V  =  7.56 V

   
   

   and since V_SUPPLY = V_C + V_R:

   
   

   V_R  =  V_SUPPLY  -  V_C  =  12 V  -  7.56 V  =  4.44 V

   
   
   
   b. the switch has been in position B for 5 seconds?
   
   

   When the switch is moved to position B, the battery is no longer part of the circuit and the capacitor starts to discharge through the resistor. Five seconds after the switch is moved to position B, the capacitor voltage will have fallen to 0.37 of the voltage it had at the instant the switch was moved from position A to position B (7.56 V). The new instantaneous voltage is therefore given by:

   
   

   V_C  =  0.37  ×  7.56 V  =  2.7972 V

   
   

   The instantaneous voltage drop across the resistor is the same as the capacitor voltage, and is given by:

   
   

   V_R  =  V_C  =  2.7972 V

   
   
   
3. Complete the time constant table shown below.
   
   
   
   

   C	R	Time Constant
   1 μF	1 MΩ	1 second
   1000 μF	1 kΩ	1 second
   0.22 μF	150 kΩ	0.033 seconds
   10 μF	47 kΩ	0.47 seconds

   
   
   
   
4. A 1.5 V battery is connected to a 1,000 μF capacitor in series with a 150 Ω resistor.
   
   
   a. What is the maximum current that flows through the resistor during charging?
   
   

   The maximum current flows at the instant the circuit is first connected to the battery, and is given by:

   
   

   I  =	VSUPPLY	=	1.5 V	=  0.01 mA
   	R		150 kΩ

   
   
   
   b. What is the maximum charge on the capacitor?
   
   

   The maximum charge on the capacitor occurs when the potential difference across the capacitor is equal to the supply voltage, and is given by:

   
   

   Q  =  V_SUPPLY  ×  C  =  1.5 V  ×  1000 μF  =  1500 μC

   
   
   
   c. How long does the capacitor take to reach a potential of 1.0V?
   
   

   One volt is exactly two thirds of the supply voltage (1.5 V). Since the capacitor voltage will have reached approximately two thirds of the supply voltage after one time constant (T), the approximate time required for the capacitor to reach a potential of 1.0 V will be:

   
   

   T  =  C  ×  R  =  1000 μF  ×  150 Ω  =  0.15 seconds