Introduction
The physical sciences are highly quantitative in nature. Physicists, for example, ask questions like "how fast does light travel?" or "how much mass does the sun lose in one second" or "how much energy is required to melt one cubic metre of ice?" This last question is actually quite a topical one, given that a number of scientists are currently investigating the possible effects of global warming. The answers to these and many similar questions will be in the form of a quantity.
A quantity is some property of something (a physical entity of some kind, a substance, or an effect) that can be measured. Expressing a quantity usually involves two components. The first is a number that tells us how much of something we are looking at. The second is a unit of measurement that tells us what kind of quantity we are looking at. A unit of measurement used to describe a quantity is sometimes referred to as a dimension. Note that some quantities, for example relative atomic mass (the ratio of the average mass of atoms of an element to one-twelfth of the mass of an atom of carbon-12), do not have an associated unit and are thus said to be dimensionless.
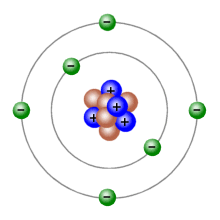
A carbon-12 atom has six protons, six neutrons and six electrons
The language in which the theories and principles of physics are expressed is mathematics. However, whereas mathematicians are primarily concerned with the properties of the numbers themselves, physicists are more concerned with the properties of things like matter and energy. In order to quantify and differentiate between the many different manifestations of matter and energy, physicists rely on being able to express quantities using standard units of measurement.
For example, if I were to describe distances to you in terms of "furlongs" or "chains", you might actually know what I was referring to. Most students would not recognise these terms, because they are almost never used. I say almost, because the chain (22 yards or 20.12 metres) is still sometimes referred to in the game of cricket as being the distance between the wickets. The furlong is ten times the length of a chain, and is still used in horse racing to describe the distance (usually expressed using miles and furlongs) over which a race is run.
Because the scientific community consists of countless individuals from all over the world, it is vitally important that the terms used to describe physical quantities will have exactly the same meaning for all scientists. For this reason, international standards have been agreed upon for the unit of measurement to be used for each kind of quantity that scientists might want to measure or describe (in other words, pretty much everything).
In these pages we will, unless otherwise stated, refer to units of measurement as defined by the International System of Units. These units are known as SI units because the name of the system in French is Système International d'unités. SI units have been widely used since the 1960s, and are based on a metric system of measurement. They are now used by scientific communities throughout the world.
The International System of Units defines seven basic quantities that include length, time and mass. Other quantities (called derived quantities) can be expressed as some combination of one or more basic quantities. Quantities such as area and volume, for example, can be derived from length. The area of a rectangle is the product of two dimensions, both of which are lengths. Similarly, the volume of a cuboid is the product of three dimensions, all three of which are also lengths. Speed is expressed as the ratio of the distance moved by an object and the time interval over which this movement takes place. Speed is therefore expressed using a combination of two basic quantities, length and time.

Speed is the ratio of distance and time
The units used to express a physical quantity are defined with reference to some exemplar or point of reference. In the case of mass, for example, the base unit is the kilogram. For a long time, one kilogram was defined as the mass of a cylinder, composed of ninety percent platinum and ten percent iridium, that resides in a vault at the International Bureau of Weights and Measures at Sèvres, near Paris. A number of official copies are held in other locations around the world, all under tightly controlled conditions.
It has emerged in recent years, by comparing the original with its copies (which is done periodically for verification purposes), that a tiny change in mass has occurred in the original, and the method of defining the kilogram was reviewed in 2016 as a result. The kilogram is now defined in terms of three fundamental physical constants - the speed of light c, a specific atomic transition frequency ΔνCs, and the Planck constant h. The new definition was approved by the General Conference on Weights and Measures (CGPM) in November 2018.
The base unit of length is the metre, which until 1983 (and for almost a hundred years prior to that) was defined as the distance between two lines etched on a platinum-iridium bar, also residing in a vault at the International Bureau of Weights and Measures. The distance must be measured when the bar is at a temperature equal to the melting point of ice. In 1983, the metre was redefined as the distance travelled by light in a vacuum in a time interval of 1/299 792 458 of a second.
The second, of course, is the base unit of time, and it too has been redefined. For almost a thousand years, up until the 1960s, the second was defined as 1/86 400 of a mean solar day. Because the gravitational forces exerted by the Moon on the Earth (and vice-versa) are causing the length of the solar day to gradually increase over time, the second is now defined as the time required for 9 192 631 770 cycles of a specific frequency in the emission spectrum of caesium-133. Derived quantities such as speed have their own units, known as derived units. The derived unit for speed is metres per second.

Gravitational forces are causing the length of the solar day to increase
Image Credit: NASA
The purpose of redefining the standards for base units is to ensure that the values chosen are constant, cannot be affected by changes in environmental conditions, and can be reproduced in any suitable equipped scientific facility with uniform accuracy.
In recent decades, physics has been delving into the farthest reaches of space and investigating the behaviour of elemental particles whose very existence has only been theorized. The success of these ongoing efforts is dependent on the ability to make extremely accurate measurements.
Establishing immutable standards for the base units of fundamental quantities is therefore crucial to the work of scientists. In addition to having reliable standards for base units however, it is equally important to have reliable instruments with which physical quantities can be measured.
If we want to measure the dimensions of a piece of wood or a sheet of metal, we can use conventional measuring apparatus (i.e. a ruler, measuring tape etc.) Smaller items such as small engineering components can be measured using calipers. Various kinds of caliper are available, depending on what kind of thing we want to measure. For greater distances, we can obtain very accurate results using modern instruments such as the laser rangefinder.
Measuring things such as the amplitude or frequency of an electronic signal requires sophisticated electronic equipment. An oscilloscope, for example, is used to examine the waveforms of constantly varying signals. They allow us to measure the characteristics of the waveform, such as (for periodic waveforms) the peak to peak voltage and frequency. The heart monitors used in hospitals are essentially a specialised version of the oscilloscope.

An analogue oscilloscope
Clearly, the devices and instruments used to measure some physical quantity will depend on the nature of whatever it is we want to measure. Some things, like the distance between two points or the mass of an inanimate object, can be measured directly. For other things, we need to be a bit more inventive. We can't see far enough into space to be able to see individual planets orbiting a remote star, for example. We can however detect tiny variations in the light that reaches us from the star caused by the gravitational effects of an orbiting body.
Similarly, we cannot directly measure the mass of an atom, but we can get around this using a piece of equipment called a mass spectrometer. In its simplest form, the device vaporises a sample of a material, turning it into gas. Each atom of the sample is then ionised (positively charged) by removing one or more of its electrons. The positively charged ions are then sent through a magnetic field. Because they carry a positive electrical charge, they are deflected by the magnetic field. The amount of deflection depends on the atom's mass (the smaller the mass, the greater the deflection). A detector measures the amount of deflection that has occurred, and the results are used to calculate the mass of the atom.
What may have occurred to you when reading the above is that all of the different methods, devices and instruments used to measure physical quantities will be subject to some degree of error. Sources of error include the degree of skill exercised by the person doing the measuring and the accuracy of the measuring devices and instruments. We must also take care that the results of measurements are recorded using an appropriate degree of precision.
In many cases, the measurements we take will not produce results that can be expressed in whole numbers of units. They will often have fractional components. Sometimes these fractional components will be rational numbers (i.e. numbers that can be expressed as exact fractions). When using such results in calculations we can leave them as fractions to avoid the "roundup error" that often occurs when converting a fraction to its decimal equivalent.
Sometimes, the fractional components are non-rational numbers (numbers whose value cannot be expressed exactly as a fraction). In such cases, we need to decide how many digits to record after the decimal point in order to achieve the required degree of accuracy. This may in any event be decided for us by limitations on the accuracy of the measuring equipment used. An important point here is the distinction between accuracy (the degree to which our measurement can be considered to be correct) and precision (the exactness with which the value measured is expressed).
As with most things in life, there is a degree of uncertainty attached to the process of measurement. Were our measurements accurate? Is our measuring equipment reliable? How sure can we be that the results have not been affected by factors of which we are unaware? The short answer is, we can never be one hundred percent certain of anything. There are however measures that can be taken to mitigate the risk of significant errors occurring.
One fairly obvious way is to repeat the measurements a number of times. If we repeatedly get the same result, we can at least be reasonably sure that our measurement has not been affected by some random factor. It is also helpful if we have some idea of the approximate magnitude of the result expected. If the actual result differs significantly from the expected result, then either the result is wrong or our expectations are unrealistic.
We have talked above about derived quantities (quantities that consist of some combination of base quantities). Base quantities such as length, time and mass are expressed as scalar values (a scalar value is a value that has magnitude, but not direction). Derived quantities such as speed, which is expressed as the ratio of the distance travelled by an object and the time interval over which this travel takes place, are also scalar values. However, speed alone only tells us how fast something is moving. It doesn't tell us in what direction it is moving.
A quantity that tells us both the speed and the direction of something is called a vector quantity. The combination of an object's speed and direction at any given instant is called its velocity. Velocity is a vector quantity because it has both magnitude and direction. Other vector quantities commonly encountered in physics include displacement, force and acceleration.
A number of notational conventions have been widely adopted by the scientific community for expressing quantities. Variables representing quantities of length, mass and time, for example, are commonly denoted by the lower case characters l, m and t respectively. Note that by convention, variables are printed as italic (oblique) text, while constants and other numerical values, function names, operators, subscripted labels, and indices are printed as roman (upright) text. It is also common to see the names of variables in scientific formulae printed using a serif font such as Times New Roman.
Note that indices that are also variables are usually printed as oblique text. For known quantities, we express the quantity as a number, followed by a unit. Each type of unit has a standard abbreviated form that is used in scientific formulae. For example, the abbreviation for kilogram is "kg", so a mass of five kilograms would be shown in a formula as "5 kg". Derived units, which are often expressed in terms of more than one base unit, also have a standard abbreviated form. A speed of five metres per second would be expressed as "5 m/s" or "5 m·s-1".
Units that are significantly smaller than the base unit (sometimes referred to as submultiple units) are denoted using the appropriate prefix. For example, the base unit of electrical current is the ampere (or just amp), which is abbreviated to "A". Many of the electrical currents we will come across in electrical circuits will be considerably smaller than one ampere (typically thousandths or millionths of an ampere).
We can prefix the letter "A" with a character that indicates which particular submultiple we want to represent. One thousandth of an ampere is called a milliampere, so we use the abbreviation "mA" (the lower case letter "m" is used to represent the milli prefix). One millionth of an ampere is called a microampere, so we use the abbreviation "μA". The lower case Greek letter mu is used to represent the micro prefix.
Units that are significantly larger than the base unit (called multiple units) are treated in the same way. Take electrical resistance as an example. The unit of electrical resistance is the ohm, represented in electrical formulae using the Greek upper-case letter Omega (Ω).
Resistances in electrical circuits tend to be large (typically thousands or millions of ohms). For very large resistances, we can prefix the Greek letter Omega with a character that indicates which particular multiple we want to represent. One thousand ohms is called a kilohm, so we use the abbreviation "kΩ". One million ohms is called a megohm, so we use the abbreviation "MΩ". The upper case letter "M" is used to represent the mega prefix.
The same quantity can be expressed in different ways, even using the conventional notation. Sometimes there is a good reason why you might want to do this. For example, you might want to make sure that two or more different values for electric current appearing in the same equation are expressed using the same units (amperes, milliamperes or microamperes).
The current values 1.5 amperes and 975 milliamperes would normally be written as "1.5 A" and "975 mA" respectively. If we knew that the result of a calculation involving these values was going have a value normally expressed in milliamperes, we might choose to express both values in milliamperes for the sake of clarity, e.g. "1500 mA - 975 mA = 525 mA".
Measurement is of critical importance in any the study of any science. In the study of physics, we need to know how to take measurements for many different kinds of quantities. We must be familiar with both base quantities and derived quantities, and with the units associated with each type of quantity. The International System of Units provides us with a common framework within which to carry out the measurement of diverse quantities, and allows us to express the results in a format that will be meaningful to the entire scientific community.
The nature of the quantity to be measured will determine the apparatus or instrumentation with which measurements are performed, as well as the degree of accuracy that must be achieved and the precision with which our results must be recorded. We should always be aware of the possibility of error, and take appropriate measures to ensure that if errors do occur, they can be detected and rectified. Last but not least, the notational conventions for recording the results of measurements or using them in equations should be observed.
