| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Cost-benefit analysis is a process intended to determine whether the total expected benefits that will be produced as a result of implementing change outweigh the total expected cost involved. Both the benefits and the costs are usually expressed in terms of financial values, and values may be adjusted to reflect the period of time over which the costs are incurred, or the benefits realised. Whilst the monetary costs of an undertaking are usually relatively easy to determine in terms of materials, capital expenditure, overheads and the estimated cost of labour, the financial value of the benefits is often more difficult to quantify. The more tangible benefits of a venture could be manifested as a reduction in operating costs (for example, being able to maintain current output with fewer employees) or as an increase in income (for example, increasing output with no associated increase in labour costs due to improvements in process efficiency). Less tangible benefits could take the form of greater flexibility, enabling the organisation to adapt more quickly to a volatile business environment or take advantage of new technologies to market its products and services.
Cost benefit analysis is usually carried out before any decision is made as to whether or not to go ahead with the project, and it will inform that decision. The process may take into account only the financial costs and expected benefits, or it may be extended to include an analysis of the more intangible costs and benefits. Either way, because of the complex issues that are usually involved, the degree of uncertainty over the actual costs that will be incurred, and the real value of any perceived benefits, the process can at best only provide approximate figures. The estimates that are arrived at may ultimately prove to be wide of the mark. Nevertheless, it is a necessary process if the decision on whether to proceed or not is to be an informed one, and should at least identify significant cost drivers and potential benefits.
Fairly obviously, since the benefits of any undertaking cannot be realised until that undertaking has been completed and the deliverables are available for use, the costs of the project (which start to be incurred as soon as work on the project commences) will not be matched by an immediate return on investment. The financial benefits will only start to materialise at some future point in time. The period of time over which the project is adjudged to have paid for itself (i.e. covered its costs) is known as the payback period, and the point in time where the project costs have been recovered is known as the break-even point. Many organisations take the payback period into account when making a decision on whether or not to proceed with a project. If the required return on investment will take too long to achieve, the decision may be to shelve the project. Complicating the equation is the fact that the real value of a sum of money earned at some future point in time will be less than its value in the present thanks to inflation, and the fact that the money has not been working for the organisation (e.g. earning interest or financing ongoing operations) in the intervening period.
Let's look at a simple example of a cost benefit analysis. A commercial director is deciding whether or not to invest in a new computer-based customer service system. The sales department currently has only a handful of computers, and the customer service operatives are not especially computer literate, but he can see the potential value of being able to reach a significantly larger number of customers and provide more efficient customer services, and feels that the new system would enable this to happen. The director carries out a cost benefit analysis, with the results shown below. It can be seen from these figures that (providing the estimates are accurate, of course) the system would pay for itself within the first year of operation - within the first eight months, in fact.
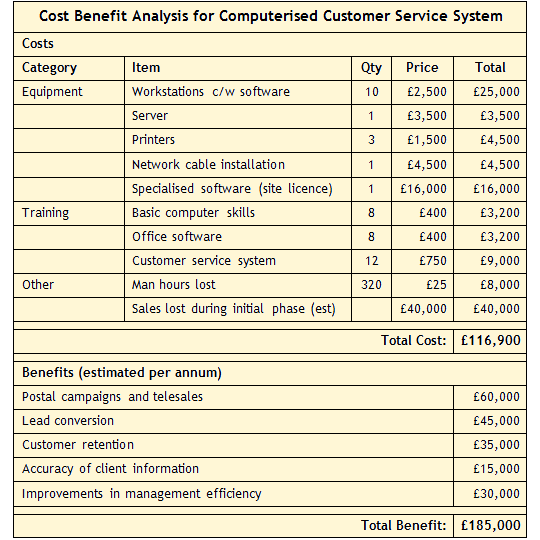
Simple example of cost-benefit analysis
Discounted cash flow (DCF) analysis is a way of calculating the value of money flowing into and out of an organisation over time (the cash flows) based on the concept of its present value. Future cash flows are estimated and then discounted to give their net present values (NPVs). The discount rate used varies, but one commonly used method of discounting is to calculate how much money would have to be invested in the present at a given rate of rate of return in order to achieve the cash flow in the future. The rate of return may be based on current interest rates plus a risk premium that reflects the risk that the future cash flow may not be forthcoming. The future value (FV) of an investment can be calculated as:
FV = NPV x (1 + i)n
Where NPV is the net present value of the future cash flow, i is the interest rate (including any risk premium), and n is the time in years until the cash flow occurs (the unit of time used can be adjusted to reflect the time within which a return on investment is anticipated). Rearranging the formula to get the net present value, we get:
NPV = FV/(1+i)n
This formula represents a relatively simplistic approach that assumes that the interest rate (including the risk premium) remains constant. The formula is applied to both positive and negative cash flows. In a typical project scenario, the cash flows are likely to be negative until some point after the project is completed. The important thing to remember is that at some point in the future (the break-even point), the NPV (represented by the sum of the discounted cash flows up to that point) should acquire a positive value (i.e. it should be greater than zero). Essentially, if the NPV has a positive value at some point the project will have paid for itself. If not, it will have lost money. To take a simple example, let's assume a project has a total cost of £100,000 over a twelve month period (Year 0). The project is expected to produce cost benefits in the form of an additional annual income of £25,000.00 per annum, and is expected to pay for itself within five years from completion of the project. If a value for i of 7.5% is used, the result will be a small positive NPV, as illustrated below (note that increasing the value of i to 8.0% results in a small negative NPV).
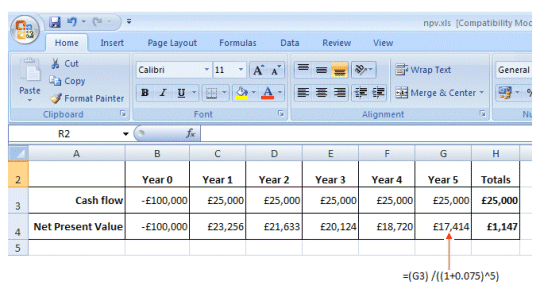
Example NPV calculation
The calculations involved can be set up in any spreadsheet program in a few minutes, enabling a range of outcomes to be calculated by varying factors such as the value of i. The notion of discounted cash flow can be used to calculate how much value a project will add to the organisation over a given period of time. If the net present value at some pre-determined future date is greater than zero, then the project has added value to the organisation. If not, there will be no point (from a financial point of view at least) in continuing with the project. The example given is a relatively simple one and has been used in order to demonstrate the basic principles. In reality such calculations can be affected by a great number of variables, but it is beyond the scope of these pages to consider the implications of this any further. Bear in mind also that even if the calculations result in an unfavourable outcome from a purely monetary point of view, the project may still have long term intangible benefits that cannot be measured in purely financial terms. There could be serious negative consequences as a result of not going ahead with a project.