Fractions
Overview
Imagine something that can be divided into equal parts. Commonly used examples include things like cakes or pizzas. Since my doctor has told me I should stay away from things like cake and pizza, I have decided to use an orange as an example. The illustration below shows an orange made up of twelve equal segments. One of the clever things about oranges is that they come already divided into equal parts (apparently oranges typically have ten segments, but they can have more).
An orange is divided into equal parts called segments
A fraction is a quantity that consists of some number of equal parts of something. Usually when we talk about fractions, we mean some quantity that is less than a whole (for example half an orange would only have six segments rather than twelve). Sometimes however we can express quantities as mixed or improper fractions (more about these later) that amount to some whole number plus a fraction. With the orange shown above, we can divide it up into various fractional parts, since we have twelve equal segments to play with. Before proceeding further, we should look at the various ways in which fractions can be expressed. For example, since we have twelve segments in total making up a whole orange, each segment can be expressed in writing as one-twelfth of an orange. I can also express this fraction as:
1/12 (one divided by twelve)
0.0833r (one-twelfth expressed as a decimal fraction)
8.33 % (one-twelfth expressed as a percentage)
This highlights another property of fractions. We can convert a what we normally think of as a fraction (for example three-quarters, or 3/4) to a decimal fraction simply by dividing the numerator by the denominator. We can do this either manually using long division, or using a calculator. In many cases however, we will have a non-terminating result (i.e. there will be an indefinite number of places after the decimal point). Whereas the fraction itself represents an exact quantity, an accurate representation of that fraction as a decimal value, or as a percentage, is not always possible. You may have to settle for a value that is rounded up or down to a given number of decimal places. For this reason, when carrying out arithmetic with fractions it is often better to calculate the answer as a fraction, and then convert that answer to its decimal equivalent (if that is what is required). This reduces the degree of error that might otherwise creep into your calculations as a result of rounding intermediate results up or down to restrict them to an acceptable number of places after the decimal point.
If you have come across fractions before (it would be very surprising if you had not), you have probably seen them represented differently from the notation used above ("1/12") which utilises a forward slash (the correct term is solidus, by the way) to separate the fraction's numerical components. Fractions represented like this are sometimes called shilling fractions, because the same format was used to express small amounts of currency under the old British imperial system of currency that used pounds, shillings and pence. Before you ask, yes I do remember using this system - I paid my bus fare to school with a three penny bit (actually, if it wasn't raining I walked to school and spent it on sweets). The advantage of writing fractions like this is that they can easily be integrated into normal electronic texts such as a word-processor document or a web page without having to jump through hoops. Fractions can also be written using a horizontal bar (or vinculum ) to separate the numbers:
| 3 |
| 4 |
Fractions written like this are sometimes referred to as "built-up" fractions, since they normally occupy more than one line on the printed page. Fractions are often seen in this format when hand-written, such as when doing calculations with fractions using pen and paper. This format does provide a degree of clarity, but can be difficult to reproduce when creating printed matter or web pages. If you are creating electronic documents containing fractions, you might want to avoid using this representation unless you feel it is absolutely necessary. Many electronic texts use graphics when providing examples of fractions written in this way. Another way or writing fractions uses a solidus to separate the numerical components (as we saw earlier), but the number to the left of the solidus appears as a superscript character, while the number to the right of the solidus is shown as a subscript. The examples below should clarify this:
1/12 (one over twelve, or one twelfth)
2/3 (two over three, or two-thirds)
3/4 (three over four, or three-quarters)
We can express these same fractions graphically, using our orange as an example:
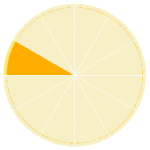
1/12 |
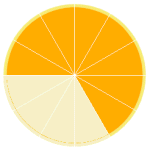
2/3 |
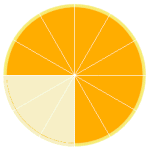
3/4 |
The kind of fraction that is expressed as one number above or to the left of another number, with a solidus or vinculum separating the two, is called a vulgar fraction (or sometimes a common fraction). This is the kind of fraction we are primarily interested in here. The two numbers that make up a vulgar fraction are called the numerator and the denominator. The numerator tells us how many equal parts we have, and the denominator tells us how many of those equal parts make up a whole. Take two-thirds (2/3) as an example. The three (as the denominator) tells us that we would need three parts of whatever it is we are talking about to make up a whole. The two (as the numerator) tells us that we actually have two such parts. We could of course use decimal fractions to represent values such as two thirds, but there would inevitably be some loss of precision (the degree of exactness), since many fractional values (of which two-thirds is a good example) cannot be expressed exactly using decimal representation. Two-thirds represented as a decimal, for example, would be 0.6666666r (you can keep adding "6" to the end of this number for as long as you like, but it will never be an exact representation of two thirds).
The numbers used in vulgar fractions (i.e. the numerator and the denominator) are always integers (whole numbers). There are three variants of the vulgar fraction. The first is called a proper fraction, in which the numerator is always less than the denominator, and the value of the fraction is less than one. The second variant is called an improper fraction (which added to the fact that it is already a vulgar fraction makes it sound altogether rather unsavoury!). This simply means however that the numerator is larger than (or possibly equal to) the denominator - for example five-thirds (5/3). The value of an improper fraction is usually greater than one, although it will be equal to one if the numerator and denominator are the same. Note that the denominator may not be zero (division of any quantity by zero results in an undefined outcome), but the numerator is allowed to be zero (in which case the fraction has a value of zero).
The third variant is called a mixed number, because it consists of some whole number plus a fraction. Instead of five-thirds for example, we could have one and two-thirds (12/3), which would be another way of representing the same value (one, of course, being equivalent to three-thirds). When carrying out arithmetic involving fractions, it is sometimes better to express mixed numbers as improper fractions in order to simplify the calculation. If we end up with a result that is still an improper fraction, we can always convert it to a mixed number. A mixed number can be converted to an improper fraction by multiplying the whole number part by the denominator of the fractional part, adding the result to the numerator of the fractional part, and discarding the whole number. For example:
| 45/8 = | 4 × 8 + 5 | = | 37 |
| 8 | 8 |
We have already talked about decimal fractions, and the fact that an exact decimal representation of some fractions is not possible. The fraction one-third (1/3), for example, can only be represented as an approximation such as "0.33", "0.333", or "0.3333". The more threes we add following the decimal point, the more accurate the representation will be, but it will never be exactly one-third. You might well also be asking yourself why it is called a decimal fraction, since it does not look anything like the vulgar fractions we normally think of when the word "fraction" is used. The reason for this apparent difference is simply that it is generally more convenient to represent decimal fractions in this way. Here are some decimal fractions, together with their vulgar fraction representation:
| 0.333 = | 333 |
| 1,000 |
| 0.5 = | 5 | = | 1 |
| 10 | 2 |
| 0.75 = | 75 | = | 3 |
| 100 | 4 |
Note two things here. First, the denominator of the decimal fraction (when we represent it as a vulgar fraction) depends on the number of places used after the decimal point. One decimal place requires a denominator of ten (so we are talking about tenths). For two decimal places, the denominator is one hundred (we are dealing with hundredths), and for three decimal places the denominator is one thousand so we are dealing with thousandths. You should see a pattern emerging here. The denominator is always some power of ten. In fact, it is always ten raised to the power of however many decimal places are used. The second point to note is that while some decimal fractions (e.g. 0.333) cannot be simplified when expressed as a vulgar fraction, others can be significantly simplified. Hence 0.75 can be represented as the familiar vulgar fraction three-quarters (3/4). Percentages (the other kind of fraction we mentioned) can be thought of as decimal fractions that always have a denominator of one hundred (100).
Simplifying fractions
In order to add or subtract fractions it is often necessary to find a common denominator (i.e. the denominator for each fraction in the expression to be evaluated must be the same). This is to ensure that we are adding or subtracting like quantities (we cannot add thirds to quarters, or subtract eighths from fifths, for example). We can easily convert each of the fractions in an expression to a different type in order to ensure that they all have the same denominator. This allows us to arrive at a result, but the fraction we end up with (or the fractional part, if the answer turns out to be a mixed number) may well not be in its simplest form. Consider a fraction like twelve-sixteenths (12/16). This can be greatly simplified by dividing both the numerator (twelve) and the denominator (sixteen) by four, to give us three-quarters (3/4). The fraction three-quarters cannot be further simplified, because there is no number other than one that will divide into both three and four. Two numbers that have this kind of relationship are said to be co-prime.
Any fraction that is not already in its simplest form can be simplified by dividing both the numerator and the denominator by their highest common factor. The highest common factor for twelve and sixteen is four, because four is the largest number that will divide exactly into both twelve and sixteen without leaving a remainder. While twelve-sixteenths is a fairly easy fraction to simplify, some of the fractions we encounter may have numerators and denominators with much higher values. Finding the highest common factor for two large numbers is often far more difficult than for relatively small numbers. Fortunately a Greek mathematician called Euclid thought up a fairly efficient and thankfully relatively simple way to derive the highest common factor for two numbers. This method is called Euclid's algorithm.
The algorithm is based on the principle that, providing both numbers are multiples of at least one common factor (other than one), the highest common factor will not change if the smaller number is subtracted from the larger number. This will result in the larger number becoming equal to or smaller than the smaller number, or zero. We continue the process of subtracting the smaller number from the larger number until one of them is zero, at which point the remaining non-zero number is the highest common factor (of course, if this turns out to be one, the fraction cannot be further simplified). We then divide the numerator and denominator of the original fraction by the highest common factor to convert the fraction to its simplest form. To demonstrate this, suppose we evaluate a sum involving fractions that gives us the result: 243/468. We can apply Euclid's theory as follows:
| HCF(468, 243) | = | HCF(468 - 243, 243) | = | HCF(225, 243) |
| HCF(225, 243) | = | HCF(243 - 225, 225) | = | HCF(18, 225) |
| HCF(18, 225) | = | HCF(225 - 18, 18) | = | HCF(207, 18) |
| HCF(207, 18) | = | HCF(207 - 18, 18) | = | HCF(189, 18) |
| HCF(189, 18) | = | HCF(189 - 18, 18) | = | HCF(171, 18) |
| HCF(171, 18) | = | HCF(171 - 18, 18) | = | HCF(153, 18) |
| HCF(153, 18) | = | HCF(153 - 18, 18) | = | HCF(135, 18) |
| HCF(135, 18) | = | HCF(135 - 18, 18) | = | HCF(117, 18) |
| HCF(117, 18) | = | HCF(117 - 18, 18) | = | HCF(99, 18) |
| HCF(99, 18) | = | HCF(99 - 18, 18) | = | HCF(81, 18) |
| HCF(81, 18) | = | HCF(81 - 18, 18) | = | HCF(63, 18) |
| HCF(63, 18) | = | HCF(63 - 18, 18) | = | HCF(45, 18) |
| HCF(45, 18) | = | HCF(45 - 18, 18) | = | HCF(27, 18) |
| HCF(27, 18) | = | HCF(27 - 18, 18) | = | HCF(9, 18) |
| HCF(9, 18) | = | HCF(18 - 9, 9) | = | HCF(9, 9) |
You can see from the above that the algorithm has correctly found the highest common factor for the numerator and denominator in our fraction to be nine (9). Dividing the numerator and denominator by nine gives us a the simplest version of our original fraction. Thus, 243/468 becomes 27/52. As you can see, this process can be somewhat long-winded. We can speed things up by using division instead of subtraction to get a remainder:
468 ÷ 243 = 1 remainder 225
243 ÷ 225 = 1 remainder 18
225 ÷ 18 = 12 remainder 9
18 ÷ 9 = 2 remainder 0
Once we have a remainder of zero, the next lowest remainder (in this case nine) becomes the highest common factor.
Adding fractions
Adding fractions is easy if the denominator of each fraction to be added is the same. Consider the following example:
| 5 | + | 1 | = | 6 | = | 3 |
| 8 | 8 | 8 | 4 |
Since we are dealing with like quantities (in this case, eighths) we can simply add the two numerators together. Note that the answer has actually been simplified from six-eighths (6/8) to three-quarters (3/4). We will look in more detail at when and how fractions can be simplified later. For now, it is only necessary to know that six-eighths has the same value as three-quarters - they are said to be equivalent fractions. The idea of equivalent fractions will help us when it comes to adding together two (or more) fractions that do not have the same denominator. What do we do, for example, when we are asked to add together two fractions of different types (thirds and quarters) as shown below?
| 2 | + | 3 | = ? |
| 3 | 4 |
We can only add fractions with the same denominator, so both of these fractions must be expressed as equivalent fractions in which both have the same denominator (i.e. a common denominator must be found). Probably the easiest way to arrive at this common denominator is to multiply the two denominators together. In this case, we have three multiplied by four, which gives us twelve (3 × 4 = 12). So far so good, but how many twelfths is each of the original fractions equivalent to? When you think about it, we have multiplied each fraction's denominator by the other fraction's denominator to arrive at the new denominator (twelve). Logic dictates therefore that we should do the same to the numerators to balance things out. Thus, the numerator from the original two-thirds becomes two multiplied by four, while the denominator from the original three-quarters becomes three multiplied by three. Here is the full calculation:
| 2 | + | 3 | = | 8 | + | 9 | = | 17 |
| 3 | 4 | 12 | 12 | 12 |
We now have an improper fraction, because the numerator is greater than the denominator. In some cases, this is what is required. In other cases, we may need to express the answer as a mixed number. In order to do this, we simply divide the numerator by the denominator so that we get a quotient and a remainder. The quotient becomes the whole number part of the mixed number, while the remainder becomes the numerator of the fractional part of the mixed number (the denominator stays as it is). Here is the result of carrying out this process for the above example:
17 ÷ 12 = 1 remainder 5 = 15/12
Note that sometimes you will end up with an improper fraction that can be simplified. Had we for example ended up with an answer of eighteen-twelfths (18/12), we could simplify this to three-halves (3/2) by dividing both the numerator and the denominator by six. Note that the same method can be used for adding three (or more) fractions. We multiply all of the denominators together to get the new common denominator. We then multiply the numerator of each of the original fractions by the product of the denominators of the other fractions. This sounds complicated. Hopefully an example will clarify matters, but first let's generalise the principle in abstract terms by expressing it algebraically. The following algebraic formula describes the process of adding just two different kinds of fractions (we have already seen how this works):
| a | + | c | = | ad + cb |
| b | d | bd |
And here is the formula for the addition of three different kinds of fractions:
| a | + | c | + | e | = | a(df) + c(bf) + e(bd) |
| b | d | f | bdf |
Now an example:
| 2 | + | 3 | + | 4 | = | 40 + 45 + 48 | = | 133 | = | 213/60 |
| 3 | 4 | 5 | 60 | 60 |
Converting the answer to a mixed number gives us two and thirteen sixtieths (213/60), which cannot be further simplified since thirteen is a prime number (it can only be divided by itself and one). In a case like this, it will probably be more meaningful to express the fractional part of the answer as a decimal fraction. We can also add mixed numbers together by applying the principles learned so far. For mixed numbers in which the fractional parts have the same denominator, we simply add the whole number parts, and then add the numerators of the fractional parts. If the result of adding the fractional parts gives us an improper fraction, we can convert it to a mixed number and add the result to the whole number addition already carried out. Here is an example:
212/3 + 332/3 = 544/3 = 551/3
If the mixed numbers have fractional parts that have different denominators, use the same method we previously used for adding fractions with different denominators to add the fractional parts of the numbers, and then add the result of this addition to the sum of the whole number parts.
Subtracting fractions
If you have understood the methods used for adding fractions, subtracting fractions should cause you few problems since the methods used are very similar. As with addition, subtracting fractions is easy if the denominator of each fraction is the same. Consider the following example:
| 5 | - | 1 | = | 4 | = | 1 |
| 8 | 8 | 8 | 2 |
Since we are dealing with like quantities (in this case, eighths) we can simply subtract the second numerator from the first. Note that the answer has actually been simplified from four-eighths (4/8) to one-half (1/2), which has the same value (i.e. it is an equivalent fraction). When we are asked to subtract one fraction from another where the fractions have different types (thirds and quarters) as shown below, we must express both fractions as equivalent fractions that have the same denominator, just as we did with addition.
| 3 | - | 1 | = ? |
| 4 | 3 |
As with addition, the easiest way to arrive at a common denominator is to multiply the two denominators together. In this case, we have four multiplied by three, which gives us twelve (3 × 4 = 12). We must next multiply each fraction's numerator by the other fraction's denominator to arrive at the numerator for each equivalent fraction. Here is the full calculation:
| 3 | - | 1 | = | 9 | - | 4 | = | 5 |
| 4 | 3 | 12 | 12 | 12 |
The answer in this case is a proper fraction and cannot be further simplified, so the answer is five-twelfths (5/12). Note that the same method can be used for subtraction involving three (or more) fractions. We multiply all of the denominators together to get the new common denominator. We then multiply the numerator of each of the original fractions by the product of the original denominators of the other fractions. Bear in mind here that subtraction with fractions has the same properties as subtraction with any other kind of number. It is, unlike addition, neither associative of commutative, so the terms cannot be arranged in a different order. The subtraction operations must also be carried out in strict left-to-right sequence. Here is an example of subtraction involving three fractions:
| 7 | - | 1 | - | 1 | = | 336 - 128 - 24 | = | 184 | = | 23 |
| 8 | 3 | 16 | 384 | 384 | 48 |
Multiplying fractions
Multiplying two fractions together is relatively straightforward. The basic procedure is to multiply the numerators (the top bits of the fractions), then multiply the denominators (the bottom bits). If necessary, the result can be simplified. An example will demonstrate how this works:
| 1 | × | 3 | = | 1 × 3 | = | 3 |
| 2 | 4 | 2 × 4 | 8 |
Multiplying a fraction by a whole number is equally straightforward. In this case, the denominator stays the same, while the numerator is multiplied by the whole number. The result can be simplified if necessary. Note that any whole number can also be written as a fraction (i.e. as itself over one), so the method shown above can be utilised as follows:
| 3 × | 3 | = | 3 | × | 3 | = | 3 × 3 | = | 9 | = 21/4 |
| 4 | 1 | 4 | 1 × 4 | 4 |
Multiplying mixed numbers by fractions, or by other mixed numbers, is also relatively straightforward. The easiest way to do this is to convert the mixed numbers to improper fractions and use the method shown above. For example:
| 31/2 × 23/4 = | 7 | × | 11 | = | 77 | = 95/8 |
| 2 | 4 | 8 |
Note that since multiplication is commutative, the order in which the fractions appear in the expression is not important. Furthermore, the same method we used above for multiplying two fractions together also works when multiplying several fractions together:
| 1 | × | 3 | × | 5 | = | 1 × 3 × 5 | = | 15 |
| 2 | 4 | 8 | 2 × 4 × 8 | 64 |
Dividing fractions
Dividing one fraction by another fraction is also relatively straightforward, since we know how to multiply fractions. This is because in order to divide one fraction (the dividend) by another (the divisor), all we need to do is multiply the dividend by the reciprocal of the divisor. The reciprocal of the divisor is found by simply inverting it (in other words, turning it upside down). For example the reciprocal of two-thirds (2/3) is three-halves (3/2), the reciprocal of three-quarters (3/4) is four-thirds (4/3), and so on. The following example illustrates how this works:
| 1 | ÷ | 3 | = | 1 | × | 4 | = | 1 × 4 | = | 4 | = | 2 |
| 2 | 4 | 2 | 3 | 2 × 3 | 6 | 3 |
Note that because division is not commutative, the order in which the fractions appear in the expression is important. In an expression involving multiple fractions, however, only the position of the first fraction must remain unchanged. The following examples illustrate this:
| 1 | ÷ | 3 | ÷ | 5 | = | 1 | × | 4 | × | 8 | = | 1 × 4 × 8 | = | 32 | = | 11/15 |
| 2 | 4 | 8 | 2 | 3 | 5 | 2 × 3 × 5 | 30 |
| 1 | ÷ | 5 | ÷ | 3 | = | 1 | × | 8 | × | 4 | = | 1 × 8 × 4 | = | 32 | = | 11/15 |
| 2 | 8 | 4 | 2 | 5 | 3 | 2 × 5 × 3 | 30 |
