Congruence and Similarity
Overview
Within the field of mathematics, and in particular geometry, congruence and similarity are related terms. Congruence essentially means that two figures or objects are of the same shape and size. Although congruent objects are identical, their orientation with respect to one another, and their physical coordinates in a plane or three-dimensional space, will often differ. For example, the two triangles shown below are both equilateral triangles and have sides of the same length. They are thus congruent, despite the triangle on the right being inverted.
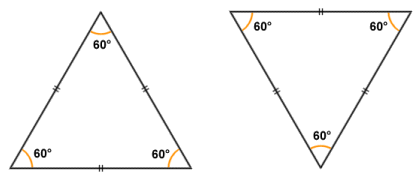
The triangles are congruent because they have the same shape and dimensions
Similarity means that two figures or objects are of the same shape, though usually not of the same size. Two circles will always be similar, for example, because by definition they have the same shape. If the circles have radii of different lengths, however, they will not be congruent.
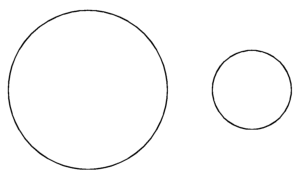
Two circles are always similar because they have the same shape
Congruence
The word congruence is derived from the Latin word congruo, which essentially means I agree. In geometry, if two objects are described as being congruent, the implication is that one can be mapped exactly to the other. In other words, they have the same shape and size, but often do not share the same location or orientation. Two congruent two-dimensional shapes, for example, may co-exist on the same plane, or be on different planes. Two congruent three-dimensional shapes may co-exist in the same three-dimensional space, but have different spatial coordinates and may be oriented differently around the x, y and z axes.
Any simple two or three-dimensional shape may be specified in terms of the x, y and (for three dimensional shapes) z coordinates of the points that define its boundaries. A circle, for example, is a two dimensional shape that has a specific centre (or origin), and a perimeter consisting of all of the points that are a given distance (the radius) from the centre on the same plane. Likewise, a triangle is a two-dimensional shape that is defined by three points on a plane. In fact, any three points on a plane can define a triangle, providing they do not all fall on the same line. A cube is defined by eight points in a three-dimensional space, while a sphere is defined by a single point in a three-dimensional space and all of the points that lie a given distance from that point in any direction.
For the remainder of this discussion, we will concern ourselves only with two-dimensional shapes, although the same principles can be applied equally well to three-dimensional objects. For any two-dimensional shape, the points that define that shape can be viewed as a mapping, because they can be specified as a set of x and y coordinates. For two shapes to be congruent, it must be possible to map one shape exactly onto the other by using a sequence of translations, rotations and reflections. Each of these terms represents some action that can be applied to a shape in order to change its location or orientation, and they will be discussed fully elsewhere. For now it is probably easiest to say that we should be able to move one shape, and if necessary turn it through an angle or flip it over, so that it lies exactly over the other shape, with all corresponding points having the same x and y coordinates.
Congruent triangles with different coordinates and orientation
Two shapes drawn at different locations on the same plane, possibly with different orientations, will obviously have different mappings. How then can we prove congruence? Actually this is relatively easy. The two mappings are congruent if, and only if, the distance between any two points in one mapping is the same as the distance between the corresponding two points in the other mapping. This definition of congruence works for any two-dimensional shape.
In the illustration below, the two irregular polygons ABCD and A'B'C'D' are congruent. If you study the image carefully, you may be able to see that if polygon ABCD is rotated clockwise through an angle of ninety degrees (90°) around point C, and then moved horizontally to the right by three squares on the grid, its points will coincide exactly with those of polygon A'B'C'D'. In order to prove congruence, it is necessary to show that the distance between any two points for polygon A'B'C'D' is the same as the distance between the corresponding two points for polygon ABCD. This includes pairs of non-adjacent points, such as A and C and A' and C'. Again, careful examination of the image should reveal that this is the case (look at the distance between two points in terms of the number of squares between them on the grid in both the horizontal and vertical directions).
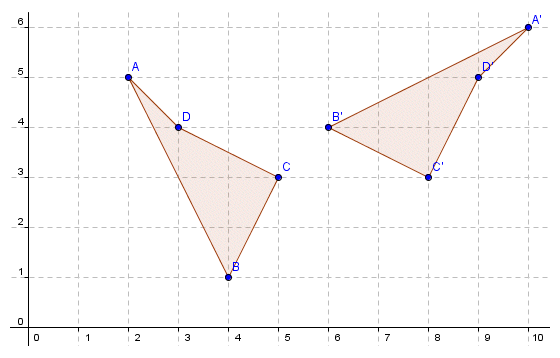
The two irregular polygons are congruent
As you can see from the above, if we take an exact copy of a two-dimensional shape and place it in a different location on the same (or on a different) two-dimensional plane, and even if we change the orientation of the shape (e.g. turn it upside down or on its side, or rotate it through some arbitrary angle) the shape remains the same. The same applies if we take a copy of some three-dimensional shape and place it elsewhere within the three-dimensional space, even if we rotate it through different arbitrarily chosen angles for all three axes. The dimensions and shape of the object remains unchanged. These properties are often referred to as invariants. Examples of invariants in congruent objects include the corresponding angles and side lengths of a triangle, the length and height of a rectangle, and the radius of a circle or sphere.
For certain two-dimensional shapes, there are other tests that can be applied in order to prove congruence. One such shape is the triangle. Two triangles are congruent if it can be shown that corresponding sides are of the same length, and corresponding angles are of the same magnitude. This involves a comparison of six attributes in total (three sides and three angles), but we can usually prove congruence using a smaller number of attributes. Congruence can often be proved if we can show that the lengths of two sides and the magnitude of a single angle, or the length of one side and the magnitude of two angles, are the same for both triangles. This does not work for all possible combinations of sides and angles, but the combinations for which it does work are described in the page entitled "Triangles". If two triangles, ΔABC and ΔDEF, are congruent, we can express this using the congruence symbol (≅):
ΔABC ≅ ΔDEF
Similarity
Similarity, like congruence, requires that two objects have exactly the same shape. For a similarity to exist, however, the dimensions need not be the same. There are a couple of implications here. The first is that, while two objects that are congruent must also, by definition, be similar, two objects that are similar need not be congruent. The second is that if two objects are similar, then the second object is either a scaled-up version or a scaled-down version of the first (or possibly even the same size, in which case the objects are also congruent). The orientation and location of the two objects is often different, but this has no bearing on whether or not they are similar. We said earlier that all circles are similar. It should also be fairly easy to see that all regular polygons of the same type will also always be similar.
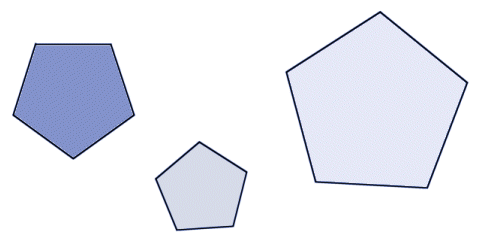
All regular polygons of the same type are similar
For two irregular polygons to be similar, all corresponding sides must vary in length by the same proportion, and all corresponding internal angles must be of the same magnitude. We have seen that we can take two congruent objects and map one to the other by a process of rotation and translation (i.e. turning one object and repositioning it so that all of its points lie over the corresponding points of the other object). We can do the same thing with two similar objects if we include the additional step of scaling one of the objects so that its dimensions match those of the other object (this must happen before any rotation and translation that may be required). The image below shows two similar non-equilateral triangles.
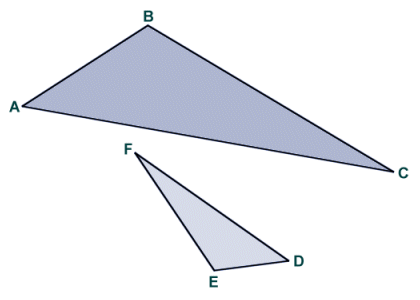
Two similar non-equilateral triangles
The triangles shown above are in fact scalene triangles (i.e. triangles in which no two angles, and no two sides, are equal). The two triangles (any two triangles in fact) can be said to be similar if the lengths of corresponding sides vary by the same proportion. With reference to triangles ABC and DEF, this can be expressed as:
| AB | = | BC | = | CA |
| DE | EF | FD |
The two triangles can also be said to be similar if it can be shown that any two corresponding angles are equal in magnitude (which would automatically require the third pair of corresponding angles to be equal in magnitude, since the internal angles of a triangle always sum to one hundred and eighty degrees):
∠ABC = ∠DEF and ∠BCA = ∠EFD
or:
∠ABC = ∠DEF and ∠CAB = ∠FDE
or:
∠BCA = ∠EFD and ∠CAB = ∠FDE
It can additionally be shown that two triangles are similar if any two corresponding pairs of sides differ in length by the same proportion, and the included angles are equal. For example:
| AB | = | BC | and ∠ABC = ∠DEF |
| DE | EF |
or:
| BC | = | CA | and ∠BCA = ∠EFD |
| EF | FD |
or:
| CA | = | AB | and ∠CAB = ∠FDE |
| FD | DE |
If triangles ABC and DEF are similar, we can express this using the similarity symbol (~):
ΔABC ~ ΔDEF
