| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Division can be thought of as the opposite to multiplication, since the expression "a divided by b", or "a ÷ b", is equivalent to "a multiplied by the reciprocal of b", or "a × 1/b". As with multiplication, there is no practical way to solve division problems using our fingers, so a basic set of "division facts" should be learnt. Children are often introduced to the concept of division at school by getting them to look at how things can be shared. For example, the teacher has ten sweets to share out between five children - how many sweets does each child get? There are also similarities between division and subtraction. Another way of looking at the sweet distribution problem is to say that every time I give each of the five children a sweet, I am subtracting five from the total (ten). How many times can I do this without giving one child more sweets than another? In this case when I have given each child two sweets I have no sweets left, so the answer is two. If I had a different number to start with (i.e. one that could not be exactly divided by five), I would have a remainder (some left over). This simplistic-sounding method is more or less how computers carry out division (they also carry out multiplication by repeated addition).
The subject of division is closely related to that of fractions, and although we will be looking at fractions elsewhere it is worth considering a few points about them here. Assuming for the moment that we are only interested in positive or negative whole numbers (signed integers), then the arithmetic operations we have looked at so far (addition, subtraction and multiplication) will all give results that are positive or negative whole numbers. Division presents us with a problem however, because the result of dividing one whole number by another will frequently give us a result that is either a fraction or has a fractional component. If I had twelve sweets (as opposed to ten) to share between five children, then I would have two sweets left over. I could express the situation in words as: "Twelve divided by five equals two, remainder two". Of course I could always eat the last two sweets myself, but then my dentist would not be happy (or come to think of it, maybe he would . . . ). The fact is that when sharing things out, whether it's sweets in the classroom or the prize money for a lottery syndicate, there will frequently be some small amount left over that can't be so easily shared.
Only in certain situations is it appropriate to express the quantity left over as a remainder. Since I was actually looking for five more sweets but only found two, I could express the leftover amount as a fraction: "Twelve divided by five equals two and two fifths." Of course, in the case of the sweets, it would be impractical (and probably quite messy) to give each child two-fifths of a sweet. The remaining sweets would therefore probably be put to one side for another occasion. In the case of a profit sharing scheme, on the other hand, I can make equal payments. I can express the amount to be paid out to each employee as an amount having a fractional part, expressed using decimal notation. Sharing a profit of twelve euros between five employees would mean I give each employee two euros and forty cents (and a stern warning not to spend it all at once). The leftover amount in this case can be expressed as a decimal fraction: "Twelve divided by five equals two point four."
You have already seen (above) the standard infix notation used for division, which features the division operator ("÷"), also known as an obelus. The operator separates the number to be divided (the dividend ) from the number it is to be divided by (the divisor ). The result of the division operation (the quotient ) appears on the right hand side of the expression following an equals sign. In algebraic equations the dividend often appears above the divisor, with a horizontal line drawn between the two. We present below a table of "division facts" for all of the possible integer divisions involving single-digit numbers. The numbers at the left-hand side of each row in the table are the dividends, while the numbers at the top of each column are the divisors. The quotient can be found at the intersection of the corresponding row and column. Note that for division of any number by three, six or nine where the result is not a whole number, the last digit shown will repeat indefinitely (it is said to be recurring). The number of times the number is actually shown depends on the precision (i.e. the degree of exactness ) required for displaying the result. We have limited the precision of the results displayed in the table to three places after the decimal point.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1.000 | 0.500 | 0.333 | 0.250 | 0.200 | 0.166 | 0.143 | 0.125 | 0.111 |
| 2 | 2.000 | 1.000 | 0.666 | 0.500 | 0.400 | 0.333 | 0.286 | 0.250 | 0.222 |
| 3 | 3.000 | 1.500 | 1.000 | 0.750 | 0.600 | 0.500 | 0.429 | 0.375 | 0.333 |
| 4 | 4.000 | 2.000 | 1.333 | 1.000 | 0.800 | 0.666 | 0.571 | 0.500 | 0.444 |
| 5 | 5.000 | 2.500 | 1.666 | 1.250 | 1.000 | 0.833 | 0.714 | 0.625 | 0.555 |
| 6 | 6.000 | 3.000 | 2.000 | 1.500 | 1.200 | 1.000 | 0.857 | 0.750 | 0.666 |
| 7 | 7.000 | 3.500 | 2.333 | 1.750 | 1.400 | 1.166 | 1.000 | 0.875 | 0.777 |
| 8 | 8.000 | 4.000 | 2.666 | 2.000 | 1.600 | 1.333 | 1.143 | 1.000 | 0.888 |
| 9 | 9.000 | 4.500 | 3.000 | 2.250 | 1.800 | 1.500 | 1.286 | 1.125 | 1.000 |
Apart from the quotients for three, six and nine which have a recurring last digit (so we already know what a higher-precision version would look like) the only other loss of precision in our table that results from limiting the quotient's output to three positions after the decimal place is for numbers divided by seven where the result is not a whole number. Essentially, any whole number with a prime number other than five or two as a factor, when used as a divisor for division operations not resulting in a whole number quotient, will produce a quotient with a fractional part that cannot be expressed as a finite decimal fraction. In the case of division by seven (or any multiple thereof), there is in fact a recurring sequence that can be seen if we extend the number of places after the decimal point sufficiently, as shown below.
1 ÷ 7 = 0.142857142857142857 (...)
1 ÷ 14 = 0.071428571428571428 (...)
There are other interesting things that we can clearly see from the above table. First of all, if the divisor is bigger than the dividend, the quotient will have a value of less than one. Secondly, if the dividend and divisor are equal, the quotient will have a value of exactly one. If the dividend is bigger than the divisor, the quotient will always be greater than one. You may feel at this point that this is stating the blindingly obvious, and maybe it is. However, you should also note that in the majority of cases the division of one single-digit number by another results in either a fraction, or a number with a fractional part. It is interesting to note the patterns that emerge. For example, dividing any whole number by three always results in a either a whole number, a number with a fractional part of one-third (.333), or a number with a fractional part of two-thirds (.666). You can find similar patterns throughout the table. More interesting is the fact that these patterns hold true even if you scale the dividend or the divisor (or both) up or down by a factor of ten, or multiple factors of ten. You can obtain the correct quotient by taking the quotient value given in the table and shifting the decimal point left or right by the appropriate number of places. Let's look at a couple of examples using the table:
6 ÷ 70 = 0.0857
300 ÷ 0.8 = 375
In the first example, I took the quotient for a dividend of six and a divisor of seven given in the table as 0.857. Because the divisor I am using is actually seventy (7 × 10) rather than seven, a tenfold increase in magnitude, the quotient will need to be reduced by a factor of ten (remember that as the divisor gets bigger in relation to the dividend, the quotient gets smaller). In the second example, I took the quotient for a dividend of three and a divisor of eight (0.375). In this example, the dividend is 3 × 102, while the divisor is 8 × 10-1. The quotient we get from the table therefore needs to be multiplied by 103 to obtain the correct value of 0.375 × 103 = 375. The reasons for this may or may not be immediately obvious to you, but think of it in terms of having divided a significantly larger dividend (a hundred times larger, in fact) by a smaller divisor (one tenth of the size).
Sometimes we are interested only in finding the whole numbers that will divide into another whole number an exact number of times without leaving any remainder. These numbers are usually called factors. Prime numbers (e.g. 5, 7, 11 etc.) are of special interest in this respect, because the only numbers that can be divided an exact number of times into a prime number without leaving a remainder are the prime number itself and one. For other numbers, it is often useful to be able to find the factors (the numbers that will divide into them an exact number of times). For any numbers up to 144, we can use the condensed version of the Twelve Times Tables (see below) as a kind of reverse lookup table to find the factors for a particular number. We can see from the illustration that the factors of fifty-six (other than one and fifty-six itself) are seven and eight, because the number fifty-six lies at the intersection of the rows and columns labelled with these numbers. It follows that the factors of both seven and eight are also factors of fifty-six, as are the factors of these factors. All of the factors of fifty-six (1, 2, 4, 7, 8, and 56) are shown highlighted in the table.
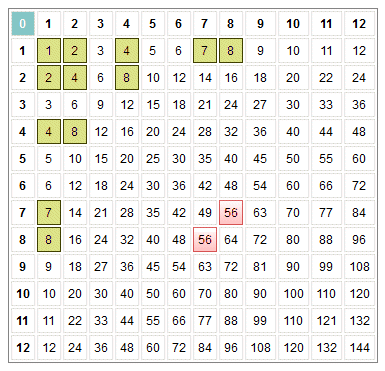
The basic multiplication facts table
Although the "division facts" we have looked at so far are useful, and familiarity with them will allow us to carry out many basic division operations as mental arithmetic, there will inevitably be occasions when somewhat more complex problems must be solved. There are of course methods available for solving these problems using pen and paper, and we will be looking at one of these ("Long Division") shortly. Before we do, there are a few more points that are of interest relating to division. First of all, we should look at divisions involving zero. Just as we can say that zero multiplied by any number equals zero, we can also state that zero divided by any number (including zero) also equals zero. Dividing any non-zero number (positive or negative) by zero is said to have an undefined outcome. In fact, if a computer programmer writes a piece of code that inadvertently results in an attempt to divide a non-zero value by zero, the most likely outcome is that the program will unceremoniously cease to function (a condition known as a crash ). Because of the way that computer logic circuits carry out division, the code essentially enters an endless loop from which it cannot exit.
Unlike multiplication, division is neither associative nor commutative. The order in which the dividend and divisor appear will obviously affect the outcome unless both numbers are the same. Furthermore, where more than two terms are involved in a single expression involving only division, the order in which each division operation is carried out is also critical to the outcome. The following expressions illustrate the point:
16 ÷ (8 ÷ 4) = 8
(16 ÷ 8) ÷ 4 = 0.5
An interesting relationship exists between division and multiplication however, in the sense that the quotient multiplied by the divisor is always equal to the dividend. This sounds (once again) like stating the blindingly obvious, but can be used to good advantage when rearranging algebraic equations. Consider the expression: "c = a ÷ b". We can use what we know about the relationship between division and multiplication to derive the following expressions:
a = b × c
b = a ÷ c
The relationship between a, b and c in the above expressions will hold true even if the terms a, b and c each represent complex expressions in their own right. Being able to rearrange the equation in this manner means that we can always isolate the term that we want to evaluate on one side of the equation (i.e. to the left or right of the equals sign).
We now come to the process of long division, which provides a means of carrying out more complex division operations (i.e. those involving relatively large numbers) using pen and paper. Let's start with a relatively easy example. We will divide eight hundred and sixty-one by seven (861 ÷ 7). We will write the problem using a specific format. The divisor (7) is written first, followed by a vertical bar (or sometimes a right-hand parenthesis), followed by the dividend with a line drawn above it as follows:
7 0 8 6 1
We will first consider whether the first digit of the dividend (eight) can be divided by seven. In this case the answer is yes. Eight divided by seven gives a result of one, but there will also be a remainder. We therefore write the result (one) above the dividend so that it is vertically aligned with the eight. Below the eight we put the result of multiplying seven by the number of times it can be divided into eight (one), which is seven. We then take the seven away from the eight to get the remainder (which is one), and write this remainder beneath the seven, separated from it by a horizontal line. We then bring down the next digit of the dividend (six) and place it to the right of the one. Our long division calculation now looks like this:
0 0 1
7 0 8 6 1
0 0 7
0 0 1 6
The next question to ask ourselves is, can sixteen be divided by seven, and if so how many times will seven go into sixteen? The answer in this case is yes it will, twice, so write the number two above the dividend directly over the six, and write the number fourteen (two multiplied by seven) below the sixteen. The remainder is found as before, by subtracting fourteen from sixteen and writing the answer (two) below the fourteen, again separated from it by a horizontal line. The next step is to bring down the last digit (one) and place it next to the two, to give us the following:
0 0 1 2
7 0 8 6 1
0 0 7
0 0 1 6
0 0 1 4
0 0 0 2 1
Seven goes into twenty-one three times. We know from having memorised the Twelve Times Tables that three multiplied by seven equals twenty-one. We can therefore write the three directly above the last digit of the dividend, and twenty-one directly below the number twenty-one at the bottom of our long division calculation. This time, the subtraction will result in zero, and there are no more digits to bring down from the dividend. Our calculation is complete, and the answer is one hundred and twenty-three. Here is the whole calculation, with the answer at the top above the dividend:
0 0 1 2 3
7 0 8 6 1
0 0 7
0 0 1 6
0 0 1 4
0 0 0 2 1
0 0 0 2 1
0 0 0 0 0
Of course the above example was somewhat contrived in the sense that we deliberately chose a dividend and divisor that would not result in any remainder. Here is another example, this time with seven (7) as the divisor and eight hundred and sixty-five (865) as the dividend:
0 0 1 2 3 R4
7 0 8 6 5 0 0
0 0 7
0 0 1 6
0 0 1 4
0 0 0 2 5
0 0 0 2 1
0 0 0 0 4
As you can see from the above, the answer is the same but this time when we bring down the last digit, subtracting twenty-one from the resulting number (twenty-five) leaves four, a number that cannot be divided by seven. Since there are no more digits to bring down, we are left with four as the remainder. This is denoted by the letter "R", followed by the number four, on the right-hand side of the answer. We do not have to accept this situation, however. Assume that we have reached the part in the calculation where we have a four at the bottom that is indivisible by seven. We can extend our calculation to include the remainder as a fractional part of the answer. Start by placing a decimal point after the three in the answer, and adding a zero next to the four:
0 0 1 2 3 .
7 0 8 6 5 0
0 0 7
0 0 1 6
0 0 1 4
0 0 0 2 5
0 0 0 2 1
0 0 0 0 4 0
We know of course that seven will divide into forty a number of times, and because we have learned the Twelve Times Tables we know that seven multiplied by five equals thirty-five. We shall therefore put a five after the decimal point, write thirty-five below the forty, subtract as before to leave five, and (since five obviously cannot be divided by seven) add a zero next to the five:
0 0 1 2 3 . 5
7 0 8 6 5 0 0
0 0 7
0 0 1 6
0 0 1 4
0 0 0 2 5
0 0 0 2 1
0 0 0 0 4 0
0 0 0 0 3 5
0 0 0 0 0 5 0
Fifty divided by seven gives us seven remainder one (seven multiplied by seven equals forty-nine). By now you should be able to see how the calculation will progress, so here are the remaining stages of the calculation, taking the answer to six places after the decimal point:
0 0 1 2 3 . 5 7 1 4 2 8
7 0 8 6 5 0 0 0 0 0 0 0
0 0 7
0 0 1 6
0 0 1 4
0 0 0 2 5
0 0 0 2 1
0 0 0 0 4 0
0 0 0 0 3 5
0 0 0 0 0 5 0
0 0 0 0 0 4 9
0 0 0 0 0 1 0
0 0 0 0 0 0 7
0 0 0 0 0 0 3 0
0 0 0 0 0 0 2 8
0 0 0 0 0 0 0 2 0
0 0 0 0 0 0 0 1 4
0 0 0 0 0 0 0 0 6 0
0 0 0 0 0 0 0 0 5 6
0 0 0 0 0 0 0 0 0 4
At this stage you can probably see that the calculation could continue indefinitely. In fact we now have another four left at the bottom of our calculation, so we can deduce that the pattern of numbers following the decimal point will now repeat itself ad infinitum. The only reason we continued the calculation beyond three places after the decimal point is so that you could see this pattern emerge. Normally (in most exam scenarios, for example) answers are only required to an accuracy of three places after the decimal point. The screenshot below shows the result of doing this calculation on the calculator included with Microsoft Windows. You can clearly see the repeating pattern, although note that the output is limited to thirteen places after the decimal point, so the last digit has been rounded up to a six.
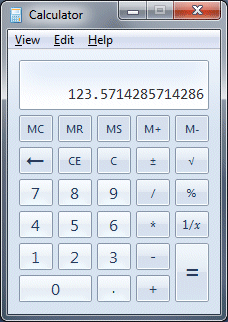
The result of calculating 865 ÷ 7 using the Ms Windows Calculator
Long division can in theory be used to carry out division operations involving very large numbers and multiple-digit divisors. The example below shows how you would go about dividing a five-digit dividend by a two-digit divisor. Note that because the divisor has two digits, we must start by looking at the number comprising the first two digits of the dividend, to see if this number can be divided by the divisor. Here is our calculation for ninety-eight thousand, seven hundred and sixty-five divided by twenty-five (98,765 ÷ 25):
0 0 0 0 3 9 5 0 . 6
2 5 0 9 8 7 6 5 0 0
0 0 0 7 5
0 0 0 2 3 7
0 0 0 2 2 5
0 0 0 0 1 2 6
0 0 0 0 1 2 5
0 0 0 0 0 0 1 5
0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 5 0
0 0 0 0 0 0 1 5 0
0 0 0 0 0 0 0 0 0
In the above example, there is again a remainder that results in a fractional part to the answer. This time however, we only need to go to one place after the decimal point to get an accurate answer. Like the other manual techniques we have looked at, long division is a useful skill to have and is essential for some exam scenarios where you are not allowed a calculator. It is often simply more convenient to use a calculator, and even before the availability of cheap pocket calculators there were simple methods for carrying out division involving very large (or very small) numbers using a slide rule or logarithmic tables. Nevertheless, you should be familiar with the technique, if only because an over-reliance on technology can sometimes lead to a blind acceptance of what a calculator or a computer tells us even if it is wrong (which it will be, of course, if someone has entered one or more of the numbers incorrectly).
It is good practice to do a rough calculation, either in your head or on a piece of paper, to check that the answers given by your favourite electronic gadget are at least in the right ball park. Taking the last calculation (98,765 ÷ 25) as an example, I could reason that since the dividend has a value that is close to one hundred thousand in magnitude, and since twenty-five goes into one hundred four times, then I could get a very rough answer by multiplying one thousand by four, which would give me four thousand. There are lots of ways to do these rough calculations, and choosing which method to use is usually a case of finding out what works best for you.