| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The factors of a whole number a are the whole numbers by which a can be divided exactly. In other words, the result of dividing a by any of its factors will be another whole number, which will itself be a factor of a. There are some whole numbers that only have two factors - the number itself and one. These numbers are called prime numbers, and they are of special interest for various reasons, some of which we will be touching on here. The multiples of a whole number a are the numbers that result when we multiply a by any other whole number. It should be obvious from this that, whereas there will always be a finite number of factors for a whole number (just two in the case of a prime number), the number of possible multiples for any given whole number cannot be quantified, since theoretically, any whole number could have an unlimited number of multiples. Two values that are of particular interest to us are the highest common factor (HCF) for two numbers (i.e. the largest number by which they can both be divided exactly), and the lowest common multiple (LCM) for two numbers, which is the smallest number that is a multiple of both numbers. We will start by looking at factors.
As we said above, the factors of a whole number a are the set of whole numbers by which a can be divided exactly. These factors will obviously include a itself, and one (indeed for prime numbers, a and one will be the only factors). For a relatively small value of a, it is easy to find all of the factors simply by going through all of the numbers from one to a, and determining whether or not they will divide exactly into a. In fact, it is only necessary to go through half of the numbers, since any number larger than a divided by two is obviously not going to be a factor of a. Let's use this (somewhat unsophisticated) method to find the factors of twelve. We already know that twelve and one are factors, so we can write these numbers on a line, at opposite ends and in numerical order (i.e. with the lowest number at the left-hand end and the highest number at the right-hand end):
1 12
Is two a factor? Yes, twelve divided by two gives us six (we know this because we know from our times tables that two multiplied by six equals twelve!), so we know that both two and six are factors. We can write these numbers on the line, so that they appear in their correct numerical order left-to-right.
1 2 6 12
Is three a factor? Yes of course, we know that twelve divided by three gives us four, so we know that both three and four are factors. We can add these numbers to the line, again making sure that they appear in their correct numerical order left-to-right.
1 2 3 4 6 12
The only number left to try is five, and you should recall from your twelve times tables that twelve is not a multiple of five, so five cannot be a factor of twelve. This highlights one of the characteristic of factors and multiples by the way, which is that any factor of a number a has a as one of its multiples. Conversely, any multiple of a number a has a as one of its factors. My apologies to those who feel I am stating the blindingly obvious, but sometimes we need to have our attention drawn to things that are "obvious", because not everybody looks at the world in the same way. Some people can see the relationships between numbers immediately, for example, while others take a little more time. You can, in theory, use the method shown above to find the factors for any number. However, as the numbers become larger this method rapidly becomes rather cumbersome, to say the least.
Fortunately, we are rarely asked to find all of the factors of a large number. It is however useful on occasion to know if a number is divisible by a particular number (say two, or three for example). To this end there are various rules we can apply to check the divisibility of one number by another, which will help us to find the factors of a number. Some of these rules are listed below.
| Divisor | A number is divisible by the divisor if: |
|---|---|
| 2 | Last digit is 0, 2, 4, 6, or 8 |
| 3 | Sum of digits in number is divisible by three (e.g. 456) |
| 4 | Number comprising last two digits is divisible by four (e.g. 312) |
| 5 | Last digit is 0 or 5 |
| 6 | Number is divisible by both two and three |
| 8 | Number comprising last three digits is divisible by eight (e.g. 123,168) |
| 9 | Sum of digits in number is divisible by nine (e.g. 8,514) |
| 10 | Last digit is 0 |
| 100 | Last two digits are both 0 |
The rule for divisibility by six highlights a more general rule, which is that if a number is divisible by two factors, it is also divisible by the product of those factors, so long as the product does not exceed the value of the number divided by two. For example, ninety is divisible by both three and five, so it must also be divisible by the product of three and five, which is fifteen (3 × 5 = 15, 90 ÷ 15 = 6).
With two notable exceptions (zero and one), all non-negative integers (whole numbers) are either prime numbers or composite numbers. A prime number, as we have mentioned before, has only two factors - the number itself, and one. The prime numbers between one and twenty include two, three, five, seven, eleven, thirteen, seventeen and nineteen (2, 3, 5, 7, 11, 13, 17, and 19). Note that neither zero nor one are considered to be prime numbers. A composite number is a number that has at least one other factor besides itself and one. The number twenty-one (21), for example has four factors - one, three, seven and twenty-one (1, 3, 7 and 21). When we express a number as a product of two or more of its factors, it is said to be factorised. We could for example factorise the number twenty-one in two ways - by expressing it as the product of one and twenty-one, or as the product of three and seven, as shown here:
21 = 1 × 21
21 = 3 × 7
We already know that a prime number is the product of itself and one. There is a fundamental theorem of arithmetic that states that all composite numbers can be written as a unique factorisation of prime numbers. In other words, any composite number can be written as the product of a set of prime number factors. The order in which these prime number factors are arranged is not important (multiplication is commutative, which means that the evaluation of an expression involving only multiplication will be the same regardless of the order in which the factors appear). The composition of the set of prime number factors that produce a particular composite number, on the other hand, is unique to that number. Furthermore, there is only one set of prime numbers that can be multiplied together to produce that number. Take the number forty-two (42) as an example. The factors of forty two are one, two, three, six, seven, fourteen, twenty-one, and forty-two (1, 2, 3, 6, 7, 14, 21, and 42). If we are allowed to use all of these factors, we can factorise forty-two in the following ways:
42 = 1 × 42
42 = 2 × 21
42 = 3 × 14
42 = 6 × 7
42 = 2 × 3 × 7
Looking at these factorisations, there is only one that involves only prime numbers (the last one, in fact). You can play around with the numbers for as long as you like, but the only set of prime numbers that can be multiplied together to produce forty-two is the set comprising two, three and seven (2, 3 and 7). In examinations, a question often crops up that asks the candidate to express a composite number as the product of prime numbers only, a process known as a prime factorisation. One way of finding the prime factors of a composite number is to systematically carry out division on the number using prime numbers, starting with the smallest prime number (which is two). An example will illustrate how this works. We will find the prime factors of the number three hundred and sixty (360) as follows:
360 ÷ 2 = 180 (2 is the first prime factor)
180 ÷ 2 = 90 (2 is the second prime factor)
90 ÷ 2 = 45 (2 is the third prime factor)
45 ÷ 3 = 15 (3 is the fourth prime factor)
15 ÷ 3 = 5 (3 and 5 are the fifth and sixth prime factors)
Let's analyse how this works. We start by dividing by two, since two is the smallest prime number. We continue by dividing the result of each division by the smallest prime number possible. When we get a result that is not an even number (forty-five), we cannot divide by two any more, so we try three (the next largest prime number), which produces a result of fifteen. Fifteen can also be divided by three, but this produces a result of five. Since five is itself a prime number, there are no more factors to find, and we can write the prime factorisation of three hundred and sixty as follows:
360 = 2 × 2 × 2 × 3 × 3 × 5
Those of you who prefer a more graphical approach to problem solving will be pleased to hear that there is a graphical method for finding the prime factors of a composite number. This method involves the creation of something called a factor tree. A factor tree is used to break a composite number down by stages into its prime factors. An example will best serve to illustrate how this works. We will use the same number as before (three hundred and sixty) to demonstrate the factor tree method. The diagram might start something like this:
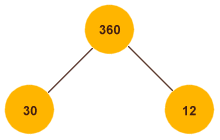
Two arbitrary factors of 360 are chosen
The circle at the top of the diagram is the root of the factor tree and contains the number we want to factorise (in this case three hundred and sixty). The two circles immediately below the root contain two factors of three hundred and sixty that, when multiplied together, produce three hundred and sixty. The choice of factors is purely arbitrary, as long as their product is three hundred and sixty, and they are both either prime or composite numbers (in other words, you can't use one). Each branch of the tree that does not already contain a prime number must itself give rise to two new branches, each of which must hold a factor of the number contained by their parent branch (i.e. the branch to which they are directly connected). The next stage of our tree might look like this:
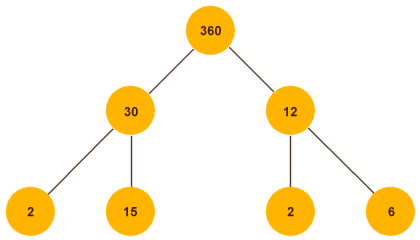
Each branch that does not contain a prime number is factorised
We now have four branches to our factor tree, although two of these now contain the number two, which is a prime number and cannot be factored further. The process continues until each branch of the tree terminates (i.e. contains a prime number and cannot be broken down any further). Here is the complete factor tree:
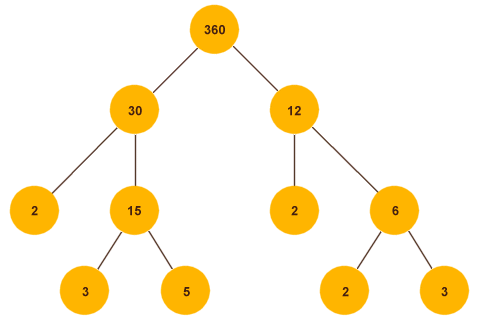
The complete factor tree for 360
Examine the end of each branch, and make a note of the prime factors. Placing them in numerical order we have two, two, two, three, three, and five (2, 2, 2, 3, 3, and 5). This is exactly the same number sequence that we found using the first method of prime factorisation. Why, though, would we want to find the prime factors of a composite number? The short answer is that this is usually just a means to an end. If we know the prime factors of two numbers, we can use that information to determine the highest common factor of those numbers - which is what we will talk about next.
If we factorise two numbers, we often find that there are certain factors that are common to both numbers. We call them common factors (what else!). Take the numbers ninety and one hundred and five (90 and 105) as an example. The factors of ninety are:
1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45 and 90
and the factors of one hundred and five are:
1, 3, 5, 7, 15, 21, 35 and 105
so the common factors for ninety and one hundred and five are:
1, 3, 5, and 15
Maybe you are familiar with fractions (you probably are but if not, have a look at the page entitled "Fractions" in this section). We are often required to re-write a fraction in order to reduce the numerator and denominator to the lowest possible values, in other words simplify the fraction as far as possible. A fraction such as "90/105" can clearly be simplified, because there are numbers that will divide into both the numerator (ninety) and the denominator (one hundred and five). The question is, since we have several options, which of the common factors should we use to simplify the fraction to the fullest extent possible? When you think about it, dividing both the numerator and denominator by the largest number possible will achieve the greatest degree of simplification. In this case, we can see from the list of common factors that the largest number we can use is fifteen. The calculation to simplify the fraction goes like this:
| 90 | = | 90 ÷ 15 | = | 6 |
| 105 | 105 ÷ 15 | 7 |
By definition then, the highest common factor (HCF) of two composite numbers is the largest number by which they can both be divided exactly, i.e. without leaving any remainder. As we have seen, one way to find the highest common factor is to list the factors of both numbers, make a separate list of the factors that appear in both lists, and take the highest number from this new list. For relatively small numbers, this works well enough. For two much larger numbers however, finding all of the common factors in this manner can be somewhat time-consuming. Fortunately, we can carry out the process more efficiently using prime factorisation.
To demonstrate the principle, we will find the highest common factor of two relatively large numbers: four hundred and ninety-five (495) and seven hundred and twenty (720). Let's start by finding the prime factors of four hundred and ninety-five (you can use whatever method you prefer, but we will use factor trees for this exercise). Here is the factor tree for four hundred and ninety-five:
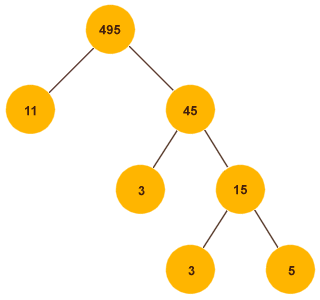
The factor tree for 495
and here is the factor tree for seven hundred and twenty:
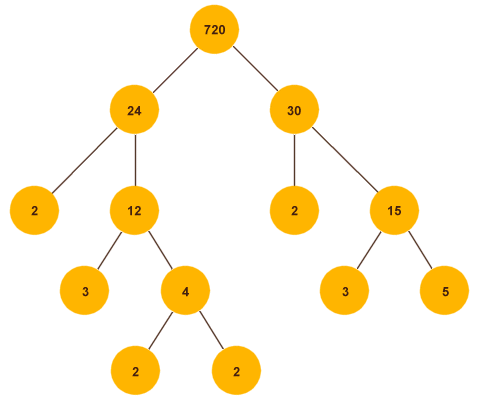
The factor tree for 720
We can now list the prime factors for each number as follows:
Prime factors of 495: 3, 3, 5, 11
Prime factors of 720: 2, 2, 2, 2, 3, 3, 5
If the two numbers have any common factors (which they obviously do, just from looking at the factor trees), then they will have at least one prime factor in common. If this is the case, the sequence of prime factors for each number will overlap at some point. We can demonstrate this overlap using a Venn diagram, as shown below (a Venn diagram is essentially used to represent the overlap between two or more sets of values).
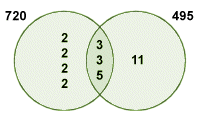
A Venn diagram showing the common prime factors for 495 and 720
The highest common factor for two numbers is the product of the prime factors they have in common (note that if the highest common factor turns out to be one, the numbers are said to be co-prime). The highest common factor for four hundred and ninety-five and seven hundred and twenty can now be calculated by multiplying together the common prime factors for the two numbers (these are the numbers shown within the intersecting area of the Venn diagram), and the result can be written formally as follows:
HCF (495, 720) = 3 × 3 × 5 = 45
The method shown above for finding the highest common factor of two numbers is not particularly efficient, especially when the numbers we are dealing with become significantly large. Furthermore, this method does not translate particularly well into an efficient computer algorithm. In the page entitled "Fractions" in this section, we make reference to the Greek mathematician Euclid, who among other things devised an efficient algorithm for deriving the highest common factor for two numbers. The algorithm is based on the principle that, providing both numbers are multiples of at least one common factor other than one, then the highest common factor will not change when the smaller number is subtracted from the larger number. The resulting number pair will still have the same highest common factor, and the smaller number is again subtracted from the larger number. The process of subtraction continues until one of the numbers is zero, at which point the remaining number is the highest common factor.
Substituting division for subtraction makes the algorithm far more efficient. With this approach, the larger number is divided by the smaller number, and the remainder becomes the smaller number for the next iteration of the cycle. When a division operation results in a remainder of zero, the remainder from the preceding division operation is the lowest common factor. Using the same pair of numbers we used to demonstrate the previous method, we can apply Euclid's algorithm as follows:
720 ÷ 495 = 1 remainder 225
495 ÷ 225 = 2 remainder 45
225 ÷ 45 = 5 remainder 0
HCF (495, 720) = 45
If we wanted to write a computer program to find the lowest common factor of two numbers, it would be relatively easy to implement Euclid's algorithm in code (for the programmers among you, the algorithm is ideal for implementation using a recursive function).
Factors and multiples and are really just two ways of looking at the same thing. A multiple of a number, a, is any number that a will divide into exactly (including itself). By definition, therefore, a is a factor of any of its multiples. For example, the first five multiples of three (3) are three, six, nine, twelve and fifteen (3, 6, 9, 12, and 15). You can see the first twelve multiples of each number from one to twelve by looking at the twelve times tables. By definition, multiplying a by any whole number will result in a multiple of a. When we apply the divisibility rules (see above) to see if one number can be divided by another, we are essentially testing to see whether the first number is a multiple of the second. Thus, according to the divisibility rules, a multiple of five must have a last digit that is either five or zero.
A number that is often of particular interest to us is the lowest common multiple (LCM) of two numbers. As the name suggests, this is the smallest number that is a multiple of both numbers. The lowest common multiple of two numbers, a and b, is often expressed as LCM (a, b). For any pair of whole numbers, there will be an indefinite number of common multiples. We could find common multiples of two numbers simply by listing a given number of multiples for each number, and finding the multiples that appeared in each list. Supposing, for example, we wanted to find the common multiples for the numbers two and three with a value of twenty or less. We can list the multiples of each number up to and including twenty (if applicable) as follows:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20
3, 6, 9, 12, 15, 18
By comparing these lists we can identify the following common factors:
6, 12, 18
Obviously if we are looking for the lowest common multiple, we can clearly see that the smallest multiple shared by both numbers is six (6). This method works reasonably well for small numbers but will become less efficient as the numbers become larger. Before proceeding to look at a more systematic approach to finding the lowest common multiple of two numbers, maybe we should consider why we would want to do this. In the page on fractions, we look at the problem of adding or subtracting fractions that have different denominators. In short, we cannot add or subtract fractions unless they have the same denominator, so we have to proceed by converting each fraction to an equivalent fraction, such that both fractions have the same denominator.
One approach is to multiply the denominators of the fractions together to obtain a common denominator. If just two fractions are being added, we then multiply the numerator of each fraction by the original denominator of the other fraction. If more than two fractions are involved, the numerator of each fraction is multiplied by the product of the original denominators of the other fractions. The problem here is that the result of our addition (or subtraction) will often be a fraction that is not in its simplest form, which means that we then have to find the highest common factor of the numerator and denominator in order to simplify the result (if this is not making sense to you at the moment, have a look at the page entitled "Fractions" for clarification). An alternative approach when performing addition or subtraction involving two fractions would be to find the highest common multiple of the fractions in order to get the lowest common denominator (as opposed to the common denominator that results from multiplying the two denominators together, which is often not the lowest common denominator). Consider the following example:
| 5 | + | 1 | = | 30 + 8 | = | 38 |
| 8 | 6 | 48 | 48 |
The denominator of the result has been obtained by multiplying the denominators of the fractions to be added. We obtain a result that is correct, but not in its simplest form. Consider this alternative version:
| 5 | + | 1 | = | 15 + 4 | = | 19 |
| 8 | 6 | 24 | 24 |
We have used the highest common factor of eight and six (twenty-four) as the denominator for the result. We then multiply the five in the first fraction by three (because the denominator eight goes into twenty-four three times), and the one in the second fraction by four (because the denominator six goes into twenty-four four times) and add them together to give us a new numerator of nineteen. This result is also correct, but is now in its simplest form. Whether this is actually a better way of tackling addition and subtraction involving fractions is probably questionable. Ultimately, you should use whatever method you find easiest. For now we will simply concentrate on how we can obtain the lowest common multiple of two numbers. As we have already seen, listing the multiples of two numbers and finding the smallest multiple they both have in common is one method, and works well enough for small numbers. What, though, if we want to find the lowest common multiple for two quite large numbers?
Think again about how we found the highest common factor of four hundred and ninety-five (495) and seven hundred and twenty (720). Here once more are the factor trees for these numbers:

The factor tree for 495

The factor tree for 720
And here are the prime factors for each number:
Prime factors of 495: 3, 3, 5, 11
Prime factors of 720: 2, 2, 2, 2, 3, 3, 5
You will recall that we constructed a Venn diagram, as shown below, to list the prime factors for each number and the overlap between them.

A Venn diagram showing the prime factors for 495 and 720
When we were attempting to determine the highest common factor for these two numbers, we were only interested in the sequence of common prime factors, the product of which gives us the highest common factor. It just so happens that the product of all of the prime factors in the Venn diagram will give us the lowest common multiple for four hundred and ninety-five and seven hundred and twenty, and the result can be written formally as follows:
HCM (495, 720) = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 11 = 7920
This expression can be written more concisely in index form (if you are unfamiliar with this notation, see the page entitled "Powers and Roots") as follows:
HCM (495, 720) = 24 × 32 × 5 × 11 = 7920
We mentioned before that the use of factor trees and Venn diagrams was not particularly efficient for finding the highest common factor (HCF) of two numbers, and does not translate particularly well into an efficient computer algorithm. We suggested using Euclid's algorithm as a more efficient method (see above). In this spirit, and based on the assumption that we are able to compute the highest common factor of two numbers, a and b, the following formula can be used to find the lowest common multiple (LCM) of a and b:
| LCM (a, b) = | a | × |b| = | b | × |a| |
| HCF (a, b) | HCF (a, b) |
The vertical bars ("|") on either side of the values a and b denote absolute values. We have already seen how to derive the highest common factor of four hundred and ninety-five and seven hundred and twenty using Euclid's algorithm, as shown below:
720 ÷ 495 = 1 remainder 225
495 ÷ 225 = 2 remainder 45
225 ÷ 45 = 5 remainder 0
HCF (495, 720) = 45
We can now apply the formula above to obtain the lowest common multiple:
| LCM (495, 720) = | 495 | × 720 = | 720 | × 495 = 7,920 |
| 45 | 45 |