| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The fundamental theorem of calculus links together the concepts underpinning the two main branches of calculus - differential calculus and integral calculus. The theorem is actually in two parts, rather imaginatively called the first fundamental theorem of calculus and the second fundamental theorem of calculus. It seems logical to start by looking at the first fundamental theorem of calculus, although be advised that, in text books and online sources dealing with the subject, there seems to be some difference of opinion among authors as to which of the two parts of the theorem is actually the first part, and which is the second.
In what appears to be the slightly more widely held view, the first fundamental theorem of calculus is the part that tells us that integration and differentiation are inverse operations. We know, for example, that taking the indefinite integral of a function gives us another function. If we then take the derivative of this second function, we get our original function back. The indefinite integral of a function is therefore said to be an antiderivative of that function. We can express this idea somewhat more formally. Suppose ƒ is a function that is continuous on the closed interval [a, b], and F is a function defined for all x in [a, b] so that:
| F(x) = | ∫ | x | ƒ(t) dt |
| a |
F will be continuous on the closed interval [a, b], differentiable on the open interval (a, b), and the following will be true for all x in (a, b):
F ′(x) = ƒ(x)
Note that we use t as the variable of integration here rather than x, because x is used as the variable upper limit of integration (apart from that, it doesn't really matter what we call the variable of integration).
The first fundamental theorem of calculus tells that if a function is continuous, it will also be integrable - i.e. it will have antiderivatives. In fact, as you may recall if you have read the page "The Indefinite Integral", it will have an infinite number of antiderivatives which differ only by a constant value known as the constant of integration. Differentiating any one of these antiderivatives will give us back our original function, because the derivative of a constant value is always zero. The same cannot be said of the reverse process. If we differentiate a function, integrating the derivative will not give us back the original function. We must always include the constant of integration C, which has an unknown value.
It is, of course, no coincidence that the area under the graph of a function - a function that represents the rate at which some quantity is changing - reflects the amount by which that quantity changes. It actually makes sense, when you think about it. Consider, for example, the relationship between speed and distance. Speed is a measure of how fast something is moving. The faster something moves, the more distance it covers in a given amount of time. Suppose a train leaves a station with a uniform acceleration of zero-point-five metres per second per second (0.5 m/s 2). How far will it actually travel in the first twenty seconds? Let's look at a graph of the speed of the train as a function of time:
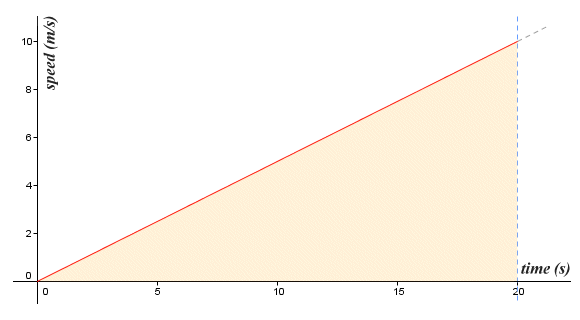
The graph of speed as a function of time with uniform acceleration of 0.5 m/s 2
Since the train is undergoing uniform acceleration, its average speed over the initial twenty second interval will be exactly half of its instantaneous speed at the twenty second mark:
Average speed = 0.5 m/s 2 × 20 s ÷ 2 = 5 m/s
And, since the distance travelled is obtained by multiplying the average speed by the elapsed time, we have:
Distance = 5 m/s × 20 s = 100 metres
This agrees with the figure we get if we calculate the area of the triangular region under the graph for the interval [0, 20]. Since the area of a triangle is calculated as base multiplied by height, all over two, and given that the speed of the train after twenty seconds will be ten metres per second (10 m/s), we have:
Area under graph = 20 × 10 ÷ 2 = 100
So, we have a speed function which we'll call ƒ(x), and which is given by:
ƒ(x) = 0.5x
If we apply the power rule for integration to ƒ(x) in order to obtain the indefinite integral F(x), we get:
| F(x) = | ∫ | 0.5x dx = 0.5 | x 2 | + C = 0.25x 2 + C |
| 2 |
This function will give us the total distance moved for a given value of x. In this particular situation, it is safe to assume that the value of C is zero, since the train is stationary when we start the clock. So, for x = 20 we have:
F(x) = 0.25 × 20 2 = 100
This is consistent with our earlier calculations. We can think of the indefinite integral F(x) as an area function. It represents the area of the region under the graph of ƒ(x) - and hence the total amount by which some quantity has changed - over the interval [0, x]. The original function ƒ(x) is the derivative of F(x). As such, it gives us the instantaneous rate of change of the quantity at some value of x within the domain of integration. It is this relationship that is defined by the first fundamental theorem of calculus.
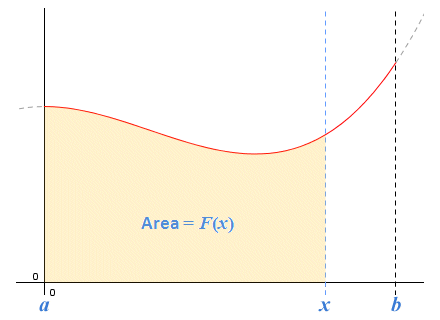
The indefinite integral can be thought of as an area function
Although the example we have used here is a linear function, you will find that the principles described apply to non-linear functions as well. They also lead us directly to the second part of the theorem.
The second fundamental theorem of calculus tells us that if a function is defined on some closed interval and is continuous over that interval, then we can use any one of its infinite number of antiderivatives to calculate the definite integral for the interval, i.e. the area of the region bounded by the graph of the function, the x axis, and the vertical lines that intersect the endpoints of the interval. We do this by evaluating the indefinite integral at the end points of the interval, and finding the difference between the resulting values. To put this a little more formally, if ƒ(x) is a continuous function defined on the closed interval [a, b], and F(x) is an antiderivative of ƒ(x), then:
| ∫ | b | ƒ(x) dx = F(b) - F(a) |
| a |
Let's go back to the example we looked at earlier, of a train leaving a station under uniform acceleration. We have already calculated how far the train moved in the initial twenty-second interval. Let's suppose that we want to find out how far our train moves in the next twenty seconds. We can do this by applying the second fundamental theorem of calculus. With any problem of this nature, the first thing we normally need to do is to find the indefinite integral F(x). In this case, we have already obtained the indefinite integral. Just as a reminder, we present it once more here:
| F(x) = | ∫ | 0.5x dx = 0.5 | x 2 | + C = 0.25x 2 + C |
| 2 |
The definite integral is therefore calculated as follows:
| ∫ | 40 | 0.5x dx = F(40) - F(20) |
| 20 |
| ∫ | 40 | 0.5x dx = (0.25 × 40 2 + C) - (0.25 × 20 2 + C) |
| 20 |
| ∫ | 40 | 0.5x dx = (400 + C) - (100 + C) = 300 |
| 20 |
So the train has moved a further three hundred metres. The illustration below shows once more the graph of the train's speed as a function of time. If you calculate the area of the shaded trapezoidal region under the graph, you will see that it is three hundred units.
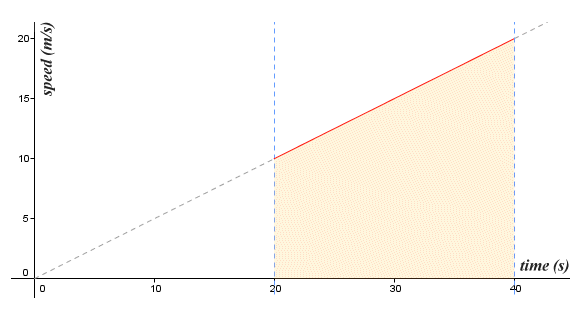
Between 20 and 40 seconds, the train moves a further 300 metres
The definite integral can be thought of as the sum of all the infinitesimal changes that have occurred over an interval. Indeed, there is another way of expressing the second fundamental theorem of calculus, known as the net change theorem, that captures this idea. The net change theorem essentially tells us that the definite integral of a function - a function that gives us the rate of change of some quantity over an interval - represents the net change in that quantity over the same interval. We know that if F(x) is the indefinite integral (antiderivative) of a function ƒ(x) defined on the closed interval [a, b], then ƒ(x) must be the derivative of F(x), i.e. ƒ(x) = F′ (x). This can be formally stated as follows:
| ∫ | b | F ′(x) dx = F(b) - F(a) |
| a |
The definite integral is a geometric concept, because it gives us the area of a bounded region under a curve. The indefinite integral, on the other hand, is an algebraic concept - it is the function that we evaluate in order to find the definite integral. When we integrate a function, we end up with an indefinite integral that includes an unknown constant of integration, C. We don't need to worry about C when calculating a definite integral, however. We will be evaluating the indefinite integral F(x) at the two end points of a closed interval [a, b] and finding the difference between the two. We know that both F(a) and F(b) will include the constant of integration C. Consequently, when we subtract F(a) from F(b), C will disappear. In fact, we can usually just leave it out of the calculation altogether.