| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
A logic gate is an electronic circuit that accepts one or more inputs, performs some kind of logical operation based on the input(s) received, and produces a single logical output. The logical operation is based on Boolean logic. Logic gates are usually implemented as digital circuits using diodes and transistors. Large numbers of logic gates are found in integrated circuits and micro-controllers.
In electronic logic circuits, inputs and outputs take the form of a voltage or current, and the output from one logic gate can be used as input to another logic gate. In fact, the output from a single logic gate can provide input for several other logic gates, although the number will limited by the physical properties of the device in question (primarily the maximum current that can be output).
The inputs and outputs for a logic gate are said to be high (a positive voltage is present) or low (zero voltage is present). A third state is possible in which the input or output exhibits high impedance, making it impossible for any significant current to flow. This is usually the case when the logic gate is in a disconnected state, and does not have any bearing on its logical operation. In most systems, a high represents the Boolean value true (1), while a low represents the Boolean value false (0).
Logic gates can be used in isolation, but are more commonly coupled together to create complex logic circuits. Some of the most common forms of logic gate are described below, together with the symbols used to denote their use on circuit diagrams (note that the "traditional" symbols are still the most widely used).
| Name | Description | Traditional Symbol | Modern Symbol |
|---|---|---|---|
| AND | An AND gate can have two or more inputs. The output is 1 only if all inputs are 1, otherwise it will be 0. | ||
| OR | An OR gate can have two or more inputs. The output is 1 if at least one of the inputs is 1. | ||
| NOT | A NOT gate has only one input. The output is 1 if the input is 0, and 0 if the input is 1. For this reason a NOT gate is also called an inverter. | ||
| NAND | NAND (NOT AND) is essentially an AND gate that has its output inverted. This time, the output is 0 only if all inputs are 1. Otherwise it will be 1. | ||
| NOR | NOR (NOT OR) is essentially an OR gate that has its output inverted. This time, the output is 0 if at least one of the inputs is 1. | ||
| XOR | An XOR (Exclusive OR) gate can only have two inputs. The output is 1 only if the inputs are different. | ||
| XNOR | XNOR (Exclusive NOR) is essentially a NOR gate that has its output inverted. This time, the output is 1 only if the inputs are the same. |
You will note from the above that most logic gates must have two or more inputs (shown above on the left-hand side) except for the NOT gate, which can have only one. Note also that the XOR and XNOR gates can only have two inputs. All logic gates have only one output (shown above on the right-hand side).
One widely used convention is to label the inputs A, B, C and so on. The output is commonly labelled Q. The small circle shown on the output of a logic gate means that the output is inverted, as you can see by comparing the symbols for the AND and NAND gates. The NAND gate is essentially an AND gate with a NOT gate applied to its output.
A truth table lists the output values that will result from all possible combinations of inputs for a particular logic gate. The symbols 1 (true) and 0 (false) are used to signify a logic high or logic low value respectively. The truth tables for the logic gates we have described are given below.
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| A | Q | |
|---|---|---|
| 0 | 1 | |
| 1 | 0 | |
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
The summary truth tables shown below give all of the possible inputs and outputs for 2-input and 3-input logic gates. Note that the XOR and XNOR logic gates cannot have more than two inputs.
| Inputs | Outputs | ||||||
|---|---|---|---|---|---|---|---|
| A | B | AND | OR | NAND | NOR | XOR | XNOR |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| Inputs | Outputs | |||||
|---|---|---|---|---|---|---|
| A | B | C | AND | OR | NAND | NOR |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Logic gates are often combined, either to create one of the other types of logic gate, or to create a more complex logic circuit. Two or more NAND gates, for example, can be used to create any other kind of logic gate. This can be quite useful, since NAND gates are relatively easy to manufacture. In the simple logic circuit below, a NOR, AND and OR gate are used in combination. A truth table can be used to determine the possible intermediate and final outputs for any combination of inputs.
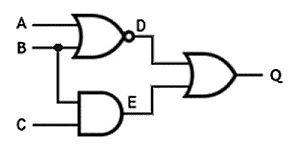
A logic circuit that uses a NOR, AND and OR gate
D = NOT (A OR B)
E = B AND C
Q = D OR E
| Inputs | Outputs | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | Q |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |