| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
A linear equation is defined as an algebraic equation in which each term is either a constant or the product of a variable and a constant, with the variable being restricted to the first power. In other words, you can have a variable such as x (= x 1), but not x 2 or x 3, or any other higher power. In addition, linear equations may not include terms that are the product of two variables (such as xy, for example). Linear equations can have one or more variables, although the ones most frequently encountered are probably those with two variables. These variables are often designated as x and y. You will often see a linear equation in two variables written in the form:
y = mx + b
This notation is called the slope-intercept form. The graph of a linear equation is a straight line (hence the name linear). The constant m will determine the slope of the line (i.e. how steeply it rises from left to right, or vice versa). The constant b determines the y-intercept (the point at which the line crosses the y axis). Linear equations are sometimes referred to as equations of the straight line. Perhaps more important to note is the fact that the slope-intercept form of the equation is sometimes written using different labels for the constants, depending on what part of the world you are in. In Australia, for example, it is written as y = mx + c. Don't let this throw you, as it is the exact same equation. Note that the slope intercept form cannot be used to describe vertical lines, since the slope would be undefined for such a line. It can however describe horizontal lines (m becomes zero, and y is therefore effectively a constant with the same value as b for any value of x). Here is the graph for the linear equation y = 0.5x + 1:
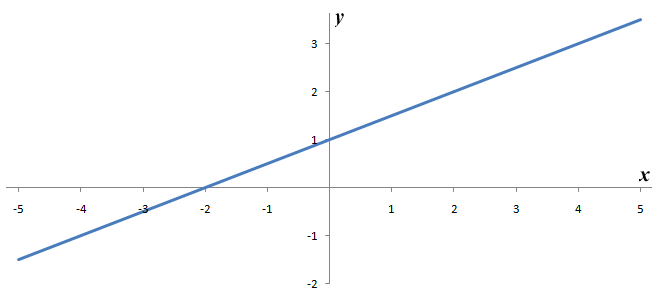
The graph of the linear equation y = 0.5x + 1
Note that the equation y = 0.5x + 1 is in the slope-intercept form, so the constant m here takes the value 0.5. For any equation in this format that has a positive value of m, the slope of the line will be positive (i.e. the line will slope upwards from left to right). If m takes a negative value, the slope will be negative (i.e. the line will slope downwards from left to right). If the slope is zero, the line will be horizontal. In the same equation, the value of b is one (1), which means that the point where the line crosses the y axis (the y-intercept) is at y = 1. If we have a graph in the form of a straight line and wish to derive an equation in the slope-intercept form (y = mx + b), we can obtain the value of b simply by finding the value of y at the point where the line intersects the y axis. The value of m can be found by getting the x and y coordinates of any two points on the line, and applying the following formula:
| m = | Δy | = | y2 - y1 |
| Δx | x2 - x1 |
The triangular symbol here (Δ), for those who are unfamiliar with it, is the capital form of the Greek letter Delta, which is used in mathematics to denote difference (as in the difference in values for y, or the difference in values for x, between two points on the line). If the line is horizontal, y2 - y1 (Δy) will equal zero, and therefore m will also equal zero. The equation y = mx + b will then describe a line that is parallel with the x axis at a distance of b above it (if b is positive) or below it (if b is negative). If we have values for m (the slope of the graph) and b (the y-intercept) we can calculate the x-intercept (the point where the line crosses the x axis) by re-arranging the slope-intercept form of the slope-intercept equation to find the value of x for which y is equal to zero. For the equation y = 0.5x + 1, this would go as follows:
0.5x + 1 = y ⇒ 0.5x + 1 = 0 ⇒ x + 2 = 0 ⇒ x = 0 - 2 = -2
What we did here was to re-arrange the equation to get y on the right-hand side, substitute 0 for y, multiply both sides by two to get rid of the rational number (0.5), and then re-arrange the equation again to get x on its own on the left-hand side. If you look once more at the graph, you can see that the answer is correct. We could, of course, find the x-intercept by checking where the line crosses the x axis on the graph, but if we are given values for m and b in an equation we can always calculate the x-intercept. This is probably going to result in a more accurate answer in cases where the values of m and b are not integers, simply because the accuracy with which we can say exactly where a line crosses an axis can vary.
The general form of the equation of a straight line is written as follows:
ax + by + c = 0
In the general form of the equation, a, b and c are integers. Either a or b may equal zero, but not both. The convention is for a to take a value that is equal to or greater than zero. Not only is the graph of this equation a straight line, but the any straight line (including the horizontal and vertical varieties) can be represented by an equation in this form. It can be shown that for the graph of an equation in this form, if b is not equal to zero, the slope of the graph will be equal to -(a/b), and the y-intercept will be equal to -(c/b). Whether these values are positive or negative will depend on whether a, b and c are positive or negative. Although y is normally the dependent variable in linear equations, we can manipulate the equation to get x on the left-hand side instead:
| ax + by + c = 0 ⇒ ax = - (by + c) ⇒ x = - | by + c |
| a |
If b is equal to zero, the equation reduces to:
| x = - | c |
| a |
If we produce a graph of this equation, we will get a vertical line at a distance of -(c/a) units away from the y-axis. The general form of the equation of a straight line (ax + by + c = 0), unlike the slope-intercept form (y = mx + b), is therefore able to represent the case of a vertical line. We can also look at what happens when y is the dependent variable.
| ax + by + c = 0 ⇒ by = - (ax + c) ⇒ y = - | ax + c |
| b |
If a is equal to zero, the equation reduces to:
| y = - | c |
| b |
If we produce a graph of this equation, we will get a horizontal line at a distance of -(c/b) units away from the x axis. The general form of the equation of a straight line is therefore also able to represent the case of a horizontal line. If a is non-zero, the x-intercept will be equal to -(c/a). Here is an example of a linear equation written in the general form:
3x + 4y - 12 = 0
In this equation, a is equal to three (a = 3), b is equal to four (b = 4) and c is equal to minus twelve (c = -12). Since x and y are both on the same side of the equation, either variable could be the dependent variable or the independent variable. We could re-arrange the equation to make y a function of x, or vice versa. From what we have established about the general form of the equation of a line however, we can determine the slope, x-intercept and y-intercept of the line (any two of which will enable us to draw the graph) as follows:
Slope = - (a/b) = - 3/4
y-intercept = - (c/b) = - (-12/4) = 3
x-intercept = - (c/a) = - (-12/3) = 4
In slope intercept form, the equation is:
y = -0.75x + 3
Here is the graph:
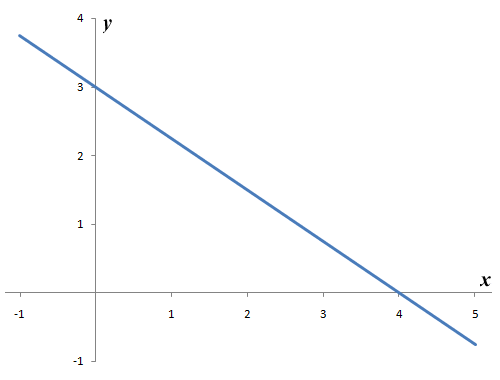
The graph of the linear equation (in general form) 3x + 4y - 12 = 0
In a system of two or more linear equations (sometimes called a linear system), the equations are related to each other by common variables. Although each equation may be different, any variable that appears in more than one of the equations will have the same value in each. Furthermore, the equations are consistent with one another in the sense that they can all be true simultaneously. In one of the simplest kinds of linear system, we are typically asked to find solutions for two equations with two variables. Take the following pair of equations as an example:
2x + 3y = 6 [1]
4x + 9y = 15 [2]
Taking either of these equations on their own, we could find any number of values for x and y that would satisfy that equation. What we want to find, however, is a pair of values that will satisfy both equations. One way in which we can proceed is to solve equation [1] for x in terms of y. We can then substitute this derived term for x into equation [2]. The revised version of the second equation will then have only one variable, and should be easy enough to solve using the standard techniques described in the page "Solving Algebraic Equations". Let's see how this works:
2x + 3y = 6 ⇒ 2x = 6 - 3y ⇒ x = 3 - 1.5y
Here, we subtracted 3y from both sides of the equation and then divided both sides of the equation by two to get x on its own on the left hand side. We can now substitute the term 3 - 1.5y for x in equation [2] as follows:
4 (3 - 1.5y) + 9y = 15 ⇒ 12 - 6y + 9y = 15 ⇒ 12 + 3y = 15
⇒ 3y = 15 - 12 ⇒ 3y = 3 ⇒ y = 1
We now have a value for y (y = 1) that we can substitute into equation [1]:
2x + 3 = 6 ⇒ 2x = 6 - 3 ⇒ 2x = 3 ⇒ x = 1.5
You can check the correctness of the solution by substituting the values of x and y into both equations and checking that they are both identities (i.e. that they are both mathematically correct statements):
2x + 3y = 6 ⇒ 3 + 3 = 6
4x + 9y = 15 ⇒ 6 + 9 = 15
We could also try a somewhat different approach to solving this linear system. The idea behind this second approach is to isolate terms involving one of the two variables on one side of the equation, and then manipulate one or both of the equations until either the left hand side or the right hand side of both equations is identical. Here are the two equations again:
2x + 3y = 6 [1]
4x + 9y = 15 [2]
We can easily re-write both equations to isolate the expressions involving x on the left-hand side of both equations as follows:
2x = 6 - 3y [3]
4x = 15 - 9y [4]
If we now multiply equation [3] by two, we get two equations in which the left hand side of the equations are identical:
4x = 12 - 6y [5]
4x = 15 - 9y [4]
Because by definition both sides of an equation are equal, then if the left-hand sides of equations [4] and [5] are equal, the right-hand sides must also be equal. Therefore we can derive a new equation with only one variable (y) as follows:
12 - 6y = 15 - 9y
Gathering like terms together we get:
3y = 3 ⇒ y = 1
We can now substitute the value obtained for y into either of the original equations to obtain a value for x. Taking equation [1] as before, we get:
2x + 3 = 6 ⇒ 2x = 6 - 3 ⇒ 2x = 3 ⇒ x = 1.5
Using this second approach, we get exactly the same solution as before, so there is no need to check the correctness of the solutions again. It would appear from the foregoing that there is only one solution for this particular system of linear equations, but this is not always the case for a linear system of two equations. There are in fact three options for such a system:
This can best be illustrated by looking at the graphical representation of a linear system. We can represent the system by drawing the graph of both equations on the same pair of axes. If there is no solution, we should see a pair of parallel lines (i.e. lines that will never meet). If there is a single solution, what we are looking for is two lines that intersect at a single point. The x and y coordinates of that point will be the values of x and y that satisfy both equations simultaneously. If there are an infinite number of solutions, the two equations will produce the same line (the two equations are effectively equivalent), and every point on the line will have x and y coordinates with values that satisfy both equations. Here is the graph for equations [1] and [2] in the above example:
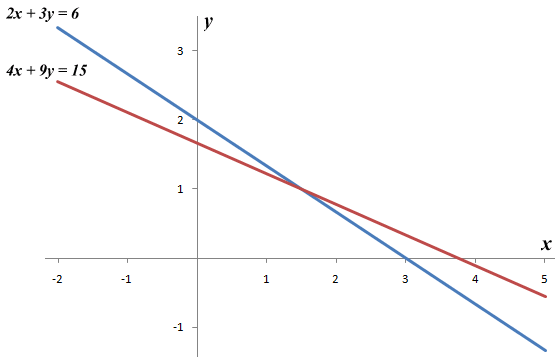
The graphs of the linear equations 2x + 3y = 6 and 4x + 9y = 15
We can see from the graphs that the two lines do indeed intersect at coordinates x = 1.5, y = 1, so there is a single solution for this particular linear system. Another way of expressing this is to say that the solution set (the set of all possible solutions) consists of the single point defined by the coordinates {1.5, 1}). Now consider the following pair of linear equations:
3x + 2y = 6 [1]
3x + 2y = 12 [2]
If the linear system has a single solution that works for all of the equations in it, the equations are said to be consistent with one another. In equations [1] and [2] above, the left-hand side of the equation in both cases is equal to 3x + 2y, which means that the right-hand side of both equations should also be equal to one another. If the equations were consistent with one another, the following statement would be true:
6 = 12
Clearly there is a problem here, since six does not equal twelve. The two equations are clearly not consistent with one another, which means that there is no solution to this particular linear system. This being the case, we would expect to see that, when we draw the graph of both equations on the same pair of axes, the resulting lines will be parallel. Here are the graphs for equations [1] and [2]:
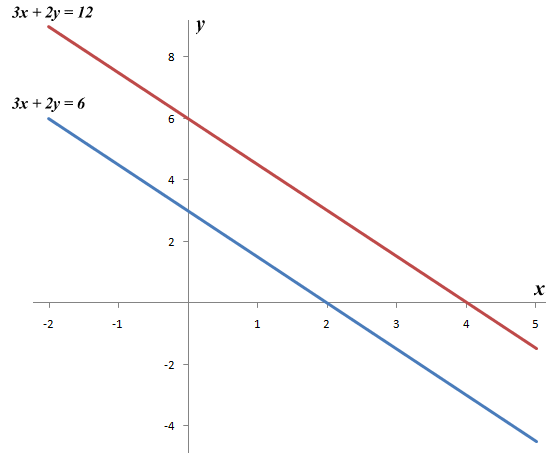
The graphs of the linear equations 3x + 2y = 6 and 3x + 2y = 12
Suppose for a moment that we are asked to solve three equations involving two variables (x and y) simultaneously. On the face of it, this is more complicated than solving two equations, but things are not always what they seem. We are looking for values of x and y that satisfy all three equations at the same time, as before. In graphical terms, the system will only have a solution if the graphs of all three equations intersect each other at a common point. When you think about it however, we only need two of the equations to find values for x and y. We will start by looking at a linear system involving three equations in two variables that does have a solution, and then examine a system that does not. Consider the following equations:
x - 2y = -1 [1]
3x + 5y = 8 [2]
4x + 3y = 7 [3]
Looking at any two of these equations in isolation, we can say that they are independent of one another, because one equation cannot be derived from the other algebraically. Note however that equation [3] is in fact the sum of equations [1] and [2], which means that any one equation in this linear system can be derived from the other two using addition or subtraction. The fact remains that if there is a single solution to a linear system involving three equations in two variables, we can always find it using just two of the equations, although it will be necessary to ensure that the values of x and y found will satisfy the third equation as well. If they do not, then there is no solution to the system. To solve the above linear system using equations [1] and [2], we will start by re-writing equation [1] to get an expression that we can substitute for x in equation [2]:
x = -1 + 2y
Now we will re-write equation [2], substituting for x:
3 (-1 + 2y) + 5y = 8
Now multiply out the brackets and gather like terms:
-3 + 6y + 5y = 8 ⇒ 11y = 11 ⇒ y = 1
Now substitute for y in equation [2]:
3x + 5 = 8 ⇒ 3x = 8 - 5 = 3 ⇒ x = 1
To check that equation [3] is satisfied by the values we have obtained for x and y, substitute these values (x = 1, y = 1) into equation [3]:
4 + 3 = 7
Since "four plus three equals seven" is a mathematically correct statement (in mathematical terms, an identity), we have found the solution set. It is a single point defined by the coordinates x = 1, y = 1. Just to underline this result, here are the graphs of all three equations drawn on a common set of axes:
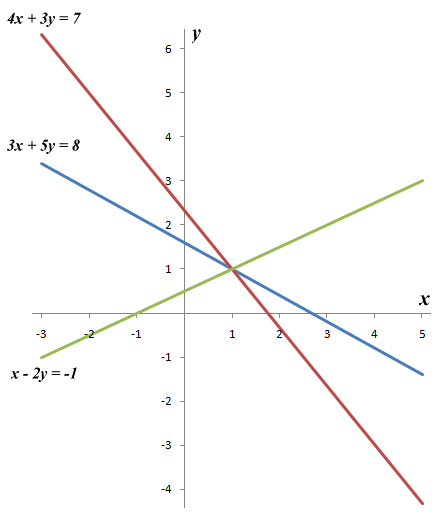
The graphs of the linear equations x - 2y = -1, 3x + 5y = 8 and 4x + 3y = 7
Now consider the following set of equations:
x + y = 1 [1]
2x + y = 1 [2]
3x + 2y = 3 [3]
The linear system defined by equations [1], [2] and [3] here does not have a solution. There appears to be an obvious inconsistency between equations [1] and [2], since x + y and 2x + y are both equal to one, but bear in mind that this is in fact possible if x equals zero. If we add equations [1] and [2] together however, we get the following:
3x + 2y = 2 [4]
If we now subtract equation [4] from equation [3], we get:
0 = 1
Clearly this statement cannot be true (in mathematical terms, it is not an identity). The linear system is therefore said to be inconsistent, and will have no solution. Just to prove the point, we present below the graphs of all three equations drawn on a common axis. There is a single solution for each pair of equations, but no solution for the system as a whole.
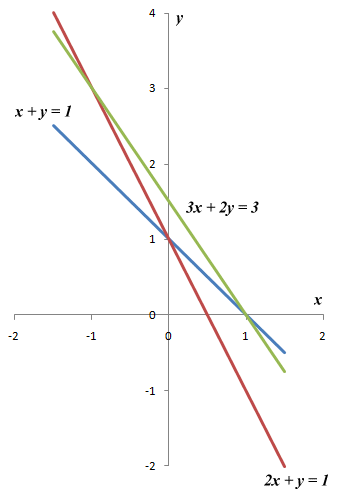
The graphs of the linear equations x + y = 1, 2x + y = 1 and 3x + 2y = 3
We will look here at solving systems of linear equations involving three equations, and three variables (x, y and z). Linear systems can involve a large number of equations, and a system consisting of up to four equations may be solved simultaneously using manual methods. Beyond that, the aid of a computer is normally required. This page is intended to be a basic introduction to linear equations, so we will not be looking at linear systems involving more than three linear equations or three variables (it should be noted, however, that quite complex systems involving non-linear equations can often be simulated using systems of linear equations). Let's suppose we have three linear equations, each involving the variables x, y and z. Our goal is to find the values of x, y and z that satisfy all three equations at the same time. Consider the following equations:
x + y - z = 4 [1]
x - 2y + 3z = -6 [2]
2x + 3y + z = 7 [3]
Our primary objective should be to reduce the complexity of the problem by reducing the number of equations and the number of variables until we have a single linear equation which we can solve using the standard methods. We can normally achieve this through a process of elimination. The choice of where to start is often somewhat arbitrary, since there are usually several possibilities. In this case, we can observe that in equation [1] we have -z, while in equation [3] we have +z. We can therefore eliminate the variable z from these equations simply by adding them together to get:
3x + 4y = 11 [4]
We can use equation [1] again, this time to eliminate z from equation [2]. First, we have to multiply equation [1] by three to get:
3x + 3y - 3z = 12 [1a]
We have labelled this equation [1a], because it is derived from, and essentially equivalent to, equation [1]. We can now add equation [2] and equation [1a] together to get:
4x + y = 6 [5]
We now have two equations instead of the original three, and have eliminated the variable z. We can now eliminate y from equations [4] and [5]. First we need to multiply equation [5] by minus four (-4) to get:
-16x + -4y = -24 [5a]
Next, we add equation [4] and equation [5a] together to get rid of y:
-13x = -13 ⇒ x = 1
We can now solve equation [4] for y by substituting one for x:
3 + 4y = 11 ⇒ 4y = 11 - 3 = 8 ⇒ y = 2
We now have values of x and y (x = 1, y = 2), so we can solve for z by substituting these values into one of the original equations. Simply because it is the first equation on the list, and for no other reason, we will use equation [1]:
x + y - z = 4 ⇒ 1 + 2 - z = 4 ⇒ -z = 4 - 3 ⇒ z = -1
The solution set is therefore x = 1, y = 2, z = -1. Because we have three variables however, we cannot represent the graphs of the three equations on a two-dimensional plane. The three-dimensional graphs of the equations would each describe a different plane, and the solution to the linear system would be the x, y, and z coordinates of the point at which all three planes intersect. The illustration below shows a three dimensional representation of the planes and the point at which they intersect (note that the planes that describe the three equations could be extended indefinitely, but we have limited the representation here to plus and minus ten units on all axes). Note that the intersection of any two planes will be a straight line. Note also that any two planes, if extended, will eventually intersect each other unless they are parallel to one another.
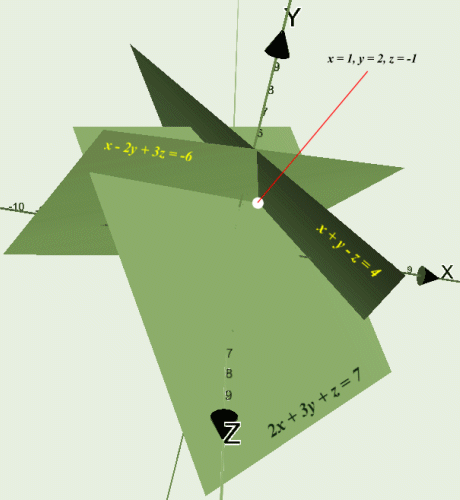
The graphs of the linear equations x + y - z = 4, x - 2y + 3z = -6 and 2x + 3y + z = 7