| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Polynomials of one kind or another occur in just about every branch of mathematics and science, in engineering and electronics, and in financial analysis. In fact they crop up just about everywhere. A polynomial expression is an algebraic expression consisting of a finite number of terms that include variables (or unknowns) and constants.
The terms of a polynomial expression may be related by addition, subtraction and multiplication operations only. The polynomial may be zero, or can be written as the sum of one or more non-zero terms. An individual term may consist of the product of a constant and one or more variables (in which case the constant is known as the coefficient of the term), or a constant on its own (in which case it is known as a constant term or simply as a constant). Coefficients may be integers, real numbers, or complex numbers (for the examples used in this page, the coefficients will all be integers).
Coefficients and constant terms are expressed as numerical values, while variables are (usually) represented by letters of the alphabet. Each variable may have an exponent, which must be a non-negative integer. The degree of a variable is the value of the exponent of that variable (if there is no exponent shown, an exponent of one is implied, and the variable has a degree of one). The degree of a term is the sum of the degrees (i.e. the exponents) of the variables it contains (the degree of a constant is zero). The degree of the polynomial is that of the term within the polynomial that has the largest degree. Consider this example of a polynomial expression:
3x 2 - 6x - 9
This polynomial expression (which you might recognise as a quadratic expression) has a single variable (x). The term with the highest degree is the quadratic (or squared) term 3x 2. This term includes a variable called x and a coefficient of three (3). The term has an exponent of two (2), which means that the variable, the term, and the expression all have a degree of two. The second term in the expression is the linear term 6x, which has a coefficient of six (6) and a degree of one (1). The last term in the expression is the constant term (or just constant) nine. The constant term has a degree of zero. Note that by convention, the terms in a polynomial expression are arranged from left to right in descending order of degree. The general form of a univariate polynomial expression (that's a polynomial expression that contains only one variable) is as follows:
anxn + an-1xn-1 + ..... + a3x3 + a2x 2 + a1x + a0
The letter a in the general form of the expression shown above represents the coefficient of each term in the expression (the final instance, a0, is the constant term). The subscripted and superscripted values in each term (n, n-1 etc.) represent the degree of the term in which they occur. Although we will not really be discussing multivariate polynomials in this page (a multivariate polynomial expression is one that contains more than one variable), it is worth noting (as mentioned above) that the degree of a term in a multivariate polynomial is equal to the sum of the degrees of each of the variables included in the term. For example, the term 4x3y 2 has a coefficient of four (4), and includes two variables, x and y. The variable x has an exponent (and hence degree) of three (3), while y has an exponent (and hence degree) of two (2). The degree of the term is therefore five (3 + 2 = 5).
Polynomials may be classified according to a number of different criteria. One way of differentiating between polynomial expressions is by the number of distinct variables they contain. A polynomial with only one variable is called univariate. Polynomials with more than one variable are called multivariate, and may additionally be classified according to the specific number of variables (bivariate for two variables, trivariate for three variables, and so on). Polynomials may also be classified by degree. The zero polynomial (which has no terms) is normally said to have a degree of minus one or minus infinity (-1 or -∞). As mentioned above, the degree of a polynomial expression is determined by whichever of its terms has the highest degree. Examples of polynomials up to the fourth degree are shown below.
Polynomials may also be classified according to the number of (non-zero) terms they contain. The zero polynomial has no terms. Polynomial expressions with one, two, and three terms are called monomial, binomial and trinomial expressions respectively. The quadratic expression 2x 2 - 3x + 4 is thus a univariate second degree trinomial expression. As mentioned above, the convention with a polynomial that has only one variable (i.e. a univariate polynomial) is for the terms to be written from left to right in descending order of degree. The coefficient of the first term must therefore be non-zero, since this is the term that determines the degree of the expression as a whole. If the coefficient of any term is zero, the term itself will evaluate to zero. Any term other than the first term is allowed to have a coefficient of zero. Such terms can effectively be removed from the expression without affecting its value. Note also that coefficients may be integers, rational numbers (fractions), real numbers, or complex numbers.
Polynomial functions take the value of one or more variables as input and produce a corresponding value as output. For a polynomial function that takes a single variable x as its input and produces an output y, there will be a single value of y for any given value of x. Successive values of x and y may be plotted as a graph to produce a smooth and continuous line or curve. The graphs of typical polynomial functions of degree zero (constant function), one (linear function), two (quadratic function), three (cubic function) and four (quartic or biquadratic function) are shown below (note that the graph of the zero polynomial, whose degree is generally considered to be undefined, is the x-axis itself).
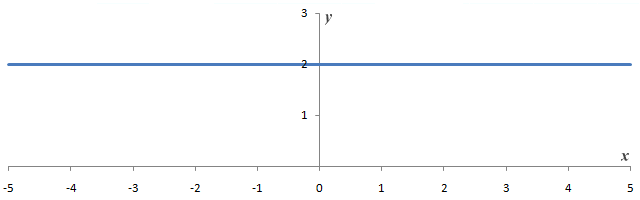
Graph of constant function y = ƒ(x) = 2
The first graph is that of the constant polynomial function y = ƒ(x) = 2, which has a degree of zero. This means that for any value of x, the output of the function ƒ(x) will be the constant value two. The graph is thus a horizontal line that intercepts the y-axis at y = 2.
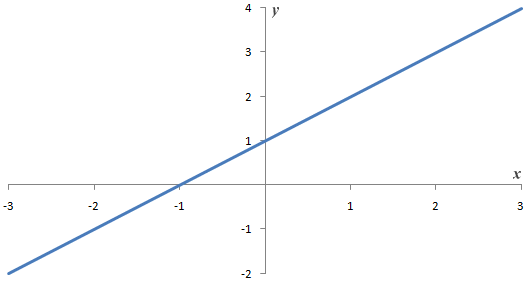
Graph of linear function y = ƒ(x) = x + 1
The second graph represents the linear polynomial function y = ƒ(x) = x + 1. A linear polynomial function is a first degree function and always produces a straight, sloping line that intersects the x-axis at a single point.
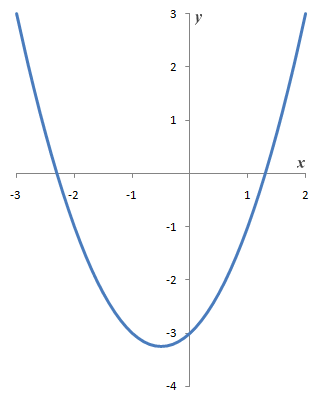
Graph of quadratic function y = ƒ(x) = x 2 + x - 3
The third graph is that of the quadratic polynomial function y = ƒ(x) = x 2 + x - 3. A quadratic polynomial function is a second degree function and always produces a parabola. The graph may intercept the x-axis at up to a maximum of two points. If the graph does intercept the x-axis, the function will have either one or two real roots (i.e. values of x for which y equals zero), depending on whether the graph crosses the x-axis at two points or just touches it at a single point. If not, the roots will be complex numbers (the subject of complex numbers will be dealt with elsewhere in these pages).
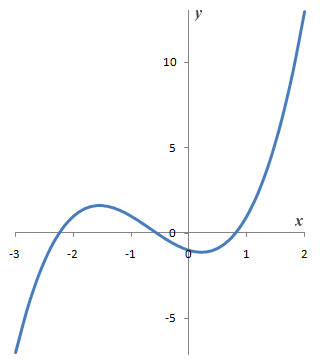
Graph of cubic function y = ƒ(x) = x3 + 2x 2 - x - 1
The fourth graph is that of the cubic polynomial function y = ƒ(x) = x3 + 2x 2 - x - 1. A cubic polynomial function is a third degree function and usually produces a curve like the one illustrated, with two critical points (points where the line changes direction). The graph may intercept the x-axis at up to a maximum of three points, and will always intercept the x-axis at least once. A cubic polynomial function will therefore always have at least one real root. In fact, a cubic function will either have three distinct real roots, a single multiple real root, or a single real root and two complex (non-real) roots.
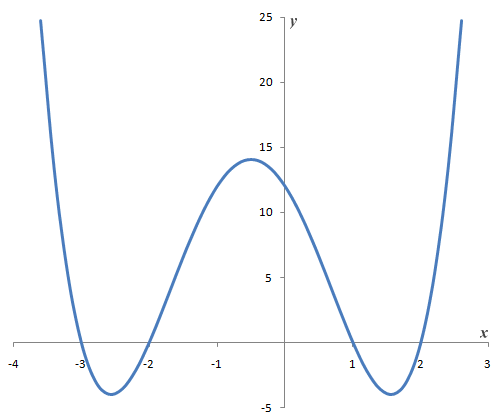
Graph of quartic function y = ƒ(x) = x4 + 2x3 - 7x 2 - 8x + 12
The fifth and final graph is that of the quartic polynomial function y = ƒ(x) = x4 + 2x3 - 7x 2 - 8x + 12. A quartic (or bi-quadratic) polynomial function is a fourth degree function and usually produces a curve like the one illustrated, with three critical points. The graph may intercept the x-axis at up to a maximum of four points, but may not intercept it at all. A quartic polynomial function will always have an even number of real or complex roots, in the sense that it will either have four real roots, two real roots and two complex roots, or four complex roots. Note that if real roots exist, they may be multiple roots.
We will not be looking at polynomials of degree five or higher, which are beyond the scope of this discussion, but you should be aware that any polynomial function with an odd-numbered degree will have at least one real root (i.e. its graph will intercept the x-axis at least once.
Polynomials can be added together using the commutative, associative and distributive laws that normally apply to arithmetic operations. Without going into lengthy explanations, this essentially means that they can be added together in any order, and like terms can be collected together. For example, supposing we had two polynomial expressions P and Q such that:
P = 5x 2 + 3x - 4xy + 7
Q = -2x 2 - x + 3y 2 - 5
We could add these expressions together as follows:
P + Q = 5x 2 + 3x - 4xy + 7 + -2x 2 - x + 3y 2 - 5
This can be simplified to give:
P + Q = 3x 2 + 2x - 4xy + 2 + 3y 2
Note that the sum of two polynomials is also a polynomial.
Polynomials can be multiplied together using the same laws as for addition. To find the product of two polynomials, we have to multiply every term of one polynomial by every term of the other polynomial. Taking the same two polynomial expressions P and Q that we used before:
P = 5x 2 + 3x - 4xy + 7
Q = -2x 2 - x + 3y 2 - 5
We could multiply these expressions together as follows:
PQ = (5x 2 · -2x 2) + (5x 2 · -x) + (5x 2 · 3y 2) + (5x 2 · -5)
+ (3x · -2x 2) + (3x · -x) + (3x · 3y 2) + (3x · -5)
+ (4xy · -2x 2) + (4xy · -x) + (4xy · 3y 2) + (4xy · -5)
+ (7 · -2x 2) + (7 · -x) + (7 · 3y 2) + (7 · -5)
This can be simplified to give:
PQ = -10x4 - 11x3 + 15x 2y 2 - 42x 2 + 9xy 2 - 8yx3 - 4x 2y + 12xy3 - 20xy - 22x + 21y 2 - 35
Note that the product of two polynomials is also a polynomial. In fact, a quadratic polynomial is the product of two linear polynomials, while a cubic polynomial is either the product of a linear polynomial and a quadratic polynomial, or three linear polynomials. The product of two or more polynomials will always be a polynomial of a degree equal to the sum of the degrees of the multiplicand polynomials.
Dividing one polynomial by another does not generally yield a polynomial (unless the divisor polynomial is a factor of the dividend polynomial). A polynomial quotient is an expression in the form of a fraction in which both the numerator and the denominator are polynomials. Such a quotient is sometimes called an algebraic fraction, but is not usually a polynomial as such. A polynomial may, however, be divided by a number, since a polynomial can have rational coefficients:
| 2x 2 + 3x - 9 | = | 2 | x 2 + x - 3 |
| 3 | 3 |
We will be looking here at various methods that can be used to solve univariate polynomial equations (i.e. polynomial equations that have a single unknown value, x). A polynomial equation is one in which one polynomial expression is set equal to another. When attempting to solve a polynomial equation for x, we are looking for one or more values of x that satisfy the polynomial function y = ƒ(x) = 0. We have already seen (above) that we can construct a graph of a polynomial function. When we attempt to solve a polynomial equation, we are looking for the value (or values) of x for which y equals zero. In other words, to solve the polynomial equation derived from a given polynomial function, we need to find the value (or values) of x at which the graph of the function intersects the x-axis. Consider the following polynomial function:
y = ƒ(x) = 3x 2 + 4x - 5
Here is the corresponding polynomial equation:
3x 2 + 4x - 5 = 0
Note that we have set the polynomial expression 3x 2 + 4x - 5 equal to zero (i.e. the zero polynomial). We must write the equation like this, with zero on the right-hand side of the equals sign, in order to be able to solve the equation (i.e. find values of x for which y equals zero). Elsewhere in these pages, we have already looked at some of the methods used to solve first-degree (linear) and second-degree (quadratic) polynomial equations, so we will concentrate here on methods of solving higher-order polynomial equations.
Before we proceed, there are a couple of points to note here. First, the number of possible solutions (or roots) for an equation increases with degree. A first-degree (linear) equation has only one solution, while a second-degree (quadratic) equation may have up to two solutions, a third-degree (cubic) equation can have up to three solutions, and so on. If both complex and multiple roots are taken into account, the number of solutions is always equal to the degree of the polynomial (this is known as the fundamental theorem of algebra). We have already mentioned the number and type of roots (e.g. real, complex, multiple etc.) that you might encounter with cubic and quartic functions (for polynomials that have two or more variables, the idea of a root does not exist, since there are usually an infinite number of possible values that variables could take that would allow the polynomial function to evaluate to zero). Secondly (and fairly obviously) while there are a number of methods of solving various kinds of polynomial equations, solutions become more difficult to find as the degree of the polynomial equations increases.
When attempting to solve a polynomial equation, the first method that should be tried is factorisation. All polynomials can be expressed in a factored form in which they are written as the product of some number of linear polynomials. Consider for example the fourth degree (quartic) function whose graph we saw above, from which we can derive the following polynomial equation:
x4 + 2x3 - 7x 2 - 8x + 12 = 0
This equation can be re-written in factored form as:
(x - 2)(x - 1)(x + 2)(x + 3) = 0
From which we can derive possible values for x (and hence the roots of the equation) of two, one, minus two and minus three (x = 2, x = 1, x = -2 or x = -3). An examination of the graph confirms that these are indeed the x-intercepts (i.e. the values of x for which y equals zero). The number of factors that need to be found will be determined by the degree of the polynomial equation. Note also that if we can find a linear factor for a high order polynomial expression, we can divide the original expression by that factor. This will result in a polynomial expression that is one degree lower than the original expression. For example, if we find a linear factor for a third degree polynomial expression, we can divide the original expression by that factor to obtain a quadratic expression. We can then either factorise the quadratic expression further to obtain the remaining roots, or apply the quadratic formula.
Note that there are also formulae available for solving cubic and quartic equations (which were originally derived in the sixteenth century), but the cubic formula is unwieldy (to say the least), and the quartic formula is the stuff of nightmares. These formulas should only be used only as a last resort, and are not dealt with in these pages. For polynomial equations of degree five and above, it was proved early in the nineteenth century that the solution of such equations is not possible using a standard algebraic formula. For those interested in investigating the cubic and quartic formulae further, there are numerous sources on the web that deal with them. The following links might be of interest:
https://planetmath.org/CubicFormula
https://planetmath.org/QuarticFormula
The first step in factorisation should always be to examine the polynomial equation to see if there are any obvious factors. Start by looking for monomial factors. A monomial factor is a single term by which all of the other terms in the polynomial expression can be divided, and takes the general form axn, where a is the (non-zero) coefficient of the term, x is the name of a variable, and n is an exponent. A monomial factor may simply consist of the constant a. Consider the following polynomial equation:
2x6 + 8x5 + 6x4 + 4x3 = 0
This can be factored as:
2x3(x3 + 4x 2 + 3x + 2) = 0
We have thus reduced a sixth degree polynomial to two factors, both of which are third degree (i.e. cubic) polynomials. The monomial factor (2x3) immediately gives us three of the roots for the original sixth degree function (x = 0 with a multiplicity of three), and simplifies the remaining third degree polynomial (we have divided all of the coefficients by two). We still have a problem in the sense that we still need to find factors for the remaining third degree polynomial. Candidate roots may not always be obvious, but there are ways and means of finding a solution.
One of the methods we can use to help us find the roots of a polynomial expression is called the rational root test. This procedure can provide us with a finite number of possible roots when we have a polynomial expression of the form:
anxn + an-1xn-1 + ..... + a3x3 + a2x 2 + a1x + a0
The rational root theorem states that if the polynomial has a rational root, and if the coefficients are all integers, then the rational root must be a fraction p/q such that p is a factor of the constant term a0, and q is a factor of the leading coefficient an. Taking the polynomial x3 + 4x 2 + 3x + 2 from the example above, we have possible values for p of one or two (1 or 2), and a single possible value for q of one (1). The rational root (if it exists) is therefore either one or two (1/1 = 1, 2/1 = 2). Of course, the number of possible rational roots increases as the possible values of p and q get larger. Consider the following expression:
2x4 - 7x3 - 3x 2 + 8x + 16
The factors of the leading coefficient are one and two (1 and 2), while the factors of the constant term are one, two, four, eight, and sixteen (1, 2, 4, 8, and 16). The possible rational roots are therefore (plus or minus) 1/2, 1/1, 2/2, 2/1, 4/2, 4/1, 8/2, 8/1, 16/2 and 16/1, which gives possible roots of (plus or minus) one half, one, two, four, eight and sixteen (±1/2, ±1, ±2, ±4, ±8 and ±16). No other rational number can be a root of the above expression.
Bearing in mind that complex numbers will be dealt with elsewhere, the focus here is on finding the real roots of high order polynomials, if they exist. Descartes' rule of signs can be used to determine the number of positive and negative real roots for a given univariate polynomial. To apply the rule, the polynomial must be written in standard form with the terms arranged in descending order of degree from left to right. What we are looking for here is any variation in sign. This means we must look at the sign (i.e. whether it is positive or negative) of the coefficient of each term, and determine whether it is the same as that of the previous term, or the opposite sign (zero coefficients may safely be ignored, since they effectively remove the term from the polynomial). To illustrate what we mean, consider the following expression:
x5 - 3x3 + 2x 2 - 5x + 8
This expression has four variations in sign. The first term (x5) has a positive coefficient (one). We then have a negative coefficient (minus three), followed by a positive coefficient (two), followed by a negative coefficient (minus five) and finally a positive constant term (eight). The sign thus varies four times in total. According to the rule of signs, the number of positive roots is either equal to the number of variations in sign, or less than the number of variations in sign by an even number (including multiple roots). Thus in the above example, the fact that we have four variations in sign means that we could have four, two or zero positive roots. We can think of the above expression as a function of x, i.e. ƒ(x) = x5 - 3x3 + 2x 2 - 5x + 8. In order to find out how many negative roots the expression might have, we need to look at the function ƒ(-x), which would negate the value of x each time it appears in our expression. We must therefore rewrite the expression as:
(-x)5 + 3(-x)3 + 2(-x) 2 - 5(-x) + 8
Simplifying this gives us:
-x5 - 3x3 + 2x 2 + 5x + 8
Note that for even-numbered exponents of x, the sign will stay the same. The possible number of negative roots can now be derived from this rewritten expression by again counting the number of variations in sign. The number of negative roots is either equal to the number of variations in sign, or less than the number of variations in sign by an even number (including multiple roots). In this case, there is only one variation in sign, so there is one negative root.
Note that the maximum possible number of positive roots plus the maximum number of negative roots is always equal to the degree of the polynomial expression, which in this case is five (5). We have already established that a polynomial equation will have a total number of roots equal to the degree of the polynomial, and that some of these roots may be complex (as opposed to real) numbers. Given that complex roots always occur in pairs for polynomial expressions with real coefficients, and that we already know that there will be one negative root for the polynomial x5 - 3x3 + 2x 2 - 5x + 8, we can summarise the possibilities in the following table:
| Positive | Negative | Complex |
|---|---|---|
| 4 | 1 | 0 |
| 2 | 1 | 2 |
| 0 | 1 | 4 |
Using the rational root test to find possible rational roots for this polynomial, we get 1/1, 2/1, 4/1 and 8/1 which gives us possible rational roots of (plus or minus) one, two, four or eight (±1, ±2, ±4 or ±8). Since the one thing we are sure of is that we have a single negative root, we could use a brute-force approach by substituting each of the negative values from our list of rational roots into the polynomial until we find one that evaluates to zero. There is however a more scientific method available. This method is called synthetic division.
Before we look at synthetic division, it is worth bearing in mind that the rational root test has certain limitations. One that we have already mentioned is that it only works if all of the coefficients are integers. Another is that it will not reveal roots that are either not rational (i.e. irrational numbers such as ±√2) or are complex numbers. A belt and braces approach to finding the roots of a polynomial can be taken in which the graph of the function is drawn, either by hand, using a graphing calculator, or in a suitable spreadsheet program. While a graph may not produce highly accurate results, it will tell you approximately where the real roots lie (assuming they exist), and how many of them there are.
Synthetic division can be used to determine whether or not a candidate root will cause a polynomial expression to evaluate to zero (i.e. whether it is indeed a root of the polynomial or not). It is a shorthand method for dividing a polynomial expression by a linear factor. If the operation is successful and the candidate is indeed a root, it will also produce the reduced polynomial (i.e. a polynomial expression one degree lower than the original expression). This should make finding the remaining roots considerably easier. Let's revisit the polynomial x5 - 3x3 + 2x 2 - 5x + 8, for which the rational root test gave us possible rational roots of (plus or minus) one, two, four or eight (±1, ±2, ±4 or ±8). We also know, thanks to the rule of signs, that there will be a single negative root. On the basis of that fact, we will use synthetic division to determine whether any of the (negative) candidate rational roots we have identified are factors of our polynomial, starting with minus one (-1).
We start the process by drawing a kind of inverted long-division symbol like the one shown below:
The candidate root is written to the left of this symbol, level with the top of the symbol, as follows:
| -1 | ||||||
The coefficients of the polynomial are written inside the symbol in line with the candidate root as shown below. Note that the terms in our polynomial include descending powers of x, from x5 down to 5x. Since there is no term involving x4 however, we must place a zero in the second column.
| -1 | 1 | 0 | -3 | 2 | -5 | 8 |
The leading coefficient is carried below the inverted long-division symbol, vertically in line with its original position:
| -1 | 1 | 0 | -3 | 2 | -5 | 8 |
| 1 |
Now we multiply the value we carried down by the candidate root, and write the result in the next column directly under the second coefficient:
| -1 | 1 | 0 | -3 | 2 | -5 | 8 |
| -1 | ||||||
| 1 |
Next, we add the values in the second column and carry the result of this addition directly below the second column:
| -1 | 1 | 0 | -3 | 2 | -5 | 8 |
| -1 | ||||||
| 1 | -1 |
Multiply the carried value by the candidate root, and write the result in the next column directly under the third coefficient:
| -1 | 1 | 0 | -3 | 2 | -5 | 8 |
| -1 | 1 | |||||
| 1 | -1 |
Now add the values in the third column and carry the result of this addition directly below the third column:
| -1 | 1 | 0 | -3 | 2 | -5 | 8 |
| -1 | 1 | |||||
| 1 | -1 | -2 |
You should see a pattern emerging here. Repeat the previous two steps to get the value beneath column four:
| -1 | 1 | 0 | -3 | 2 | -5 | 8 |
| -1 | 1 | 2 | ||||
| 1 | -1 | -2 | 4 |
Continue with the procedure to get the values beneath the last two columns:
| -1 | 1 | 0 | -3 | 2 | -5 | 8 |
| -1 | 1 | 2 | -4 | 9 | ||
| 1 | -1 | -2 | 4 | -9 | 17 |
The figure beneath the last column is the all-important one, because if it is not zero then our candidate root is, in fact, not a root of the polynomial. This synthetic division procedure tells us that if we divide the polynomial x5 - 3x3 + 2x 2 - 5x + 8 by x + 1, there will be a remainder (in this case a remainder of seventeen), so x + 1 is not a factor of x5 - 3x3 + 2x 2 - 5x + 8, which means that minus one (-1) is not a root of our polynomial. Let's try minus two (-2):
| -2 | 1 | 0 | -3 | 2 | -5 | 8 |
| -2 | 4 | -2 | 0 | 10 | ||
| 1 | -2 | 1 | 0 | -5 | 18 |
Even without carrying out the procedure for the remaining candidate roots (minus four and minus eight), it should have become apparent to you by now that we are not going to find a rational root. Drawing a graph of the function confirms that the graph does not intercept the x-axis at any of the candidate values of x. In fact, it crosses the x-axis at a value of x that lies close to minus two-point-three-three (-2.33), as shown below. Looking at this graph, it is clear that we have a single negative, non-rational real root, and four complex roots.
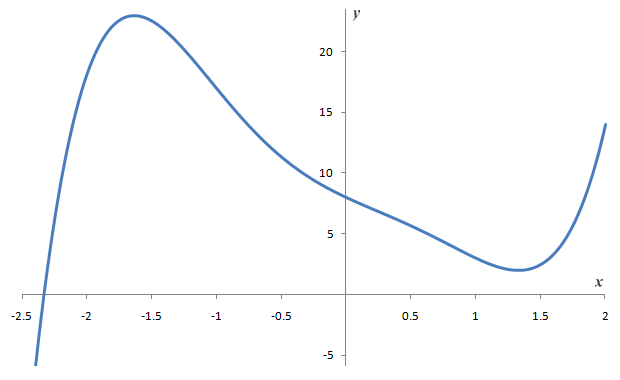
The graph of y = ƒ(x) = x5 - 3x3 + 2x 2 - 5x + 8
Even if the synthetic division process does not yield a root, it may provide us with further information about the roots that can help to narrow the search, for example by revealing upper and lower bounds for real values of x that satisfy a polynomial equation in standard form. The following general rules apply to synthetic division:
If we now carry out the synthetic division process for our third negative candidate root (which was minus four), we get the following result:
| -4 | 1 | 0 | -3 | 2 | -5 | 8 |
| -4 | 16 | -52 | 200 | -780 | ||
| 1 | -4 | 13 | -50 | 195 | -772 |
Obviously minus four is not a root of the polynomial x5 - 3x3 + 2x 2 - 5x + 8, but you may have noticed that the signs of the numbers on the bottom row alternate. According to the synthetic division rule detailed above relating to negative candidate rational roots, this means that all of the real roots of our polynomial are equal to or greater than minus four, which we can see from the graph is indeed the case. Compare that with the following example of synthetic division:
| -2 | 1 | 2 | -3 | -4 |
| -2 | 0 | 6 | ||
| 1 | 0 | -3 | 2 |
In this case, we have established that minus two is not a rational root of the polynomial because there is a remainder of two, but there is also no evidence that it represents a lower bound for the real roots. Looking at the bottom row of numbers, we have a positive value of one followed by a zero. The zero can of course be considered to be negative in this instance, but as it is followed by a negative value (minus three), this does not help us. The negative candidate root is only a lower bound if the signs of the bottom row of numbers alternate, which in this case they do not, whichever sign we choose for the zero.
We will now apply the techniques described above to solving the polynomial equation corresponding to a function that we have already seen, namely y = ƒ(x) = x4 + 2x3 - 7x 2 - 8x + 12 = 0. The equation is written in standard form as:
x4 + 2x3 - 7x 2 - 8x + 12 = 0
The expression on the left-hand side of the equation is a fourth degree polynomial. There are no obvious factors here, and certainly no monomial factors to make life easier for us. All we know for certain at this stage is that there will be four roots of one kind or another in total. This expression has two variations in sign. You may recall that, according to the rule of signs, the number of positive roots is either equal to the number of variations in sign, or less than the number of variations in sign by an even number (including multiple roots). This means that we either have two positive roots or none at all. To find out how many negative roots the expression might have, we need to look at the function ƒ(-x), which would require us to rewrite the expression as:
(-x)4 + 2(-x)3 - 7(-x) 2 - 8(-x) + 12
Simplifying this gives us:
x4 - 2x3 - 7x 2 + 8x + 12
We still have two variations in sign. Since the rule of signs tells us that the number of negative roots is either equal to the number of variations in sign, or less than the number of variations in sign by an even number (including multiple roots), there are either two negative real roots or none at all. Now we need to carry out the rational root test to see what the possible rational roots might be. This is perfectly possible, since our coefficients are all integers. Remember that the rational root must be a fraction p/q such that p is a factor of the constant term (in this case twelve), and q is a factor of the leading coefficient (which is one). There is only one possible value for q, which is one (1). Potential positive or negative rational roots therefore include all possible values of p, which gives candidate roots of (plus or minus) one, two, three, four, six and twelve (±1, ±2, ±3, ±4, ±6 and ±12).
We can now carry out synthetic division to determine which, if any, of the candidates satisfies our polynomial equation. We will begin by looking for the negative roots, starting with the candidate that has the lowest absolute value (which is minus one):
| -1 | 1 | 2 | -7 | -8 | 12 |
| -1 | -1 | 8 | 0 | ||
| 1 | 1 | -8 | 0 | 12 |
Since we have a remainder, minus one is not a rational root of our polynomial. Furthermore, the signs of the numbers on the bottom row do not alternate, so minus one does not represent a lower bound for the real roots, if they exist (bear in mind here that we have already established that there will either be two negative real roots or none at all). Let's move on to the next candidate, which is minus two:
| -2 | 1 | 2 | -7 | -8 | 12 |
| -2 | 0 | 14 | -12 | ||
| 1 | 0 | -7 | 6 | 0 |
Now we have a positive result! The remainder of zero tells us that minus two is indeed one of the roots of our polynomial. Furthermore, since there is one negative rational root there must be a second. This is borne out by the fact that the signs of the numbers on the bottom row do not alternate, so minus two is not a lower bound for the real roots of our polynomial (which we now know must exist). Let's try the next candidate, minus three:
| -3 | 1 | 2 | -7 | -8 | 12 |
| -3 | 3 | 12 | -12 | ||
| 1 | -1 | -4 | 4 | 0 |
Another positive result! The remainder of zero tells us that minus three is also one of the roots of our polynomial. Furthermore, since we have already established that there will be either exactly two negative rational roots or none at all, we can now stop looking for negative rational roots. Let's try the first positive candidate, which is one:
| 1 | 1 | 2 | -7 | -8 | 12 |
| 1 | 3 | -4 | -12 | ||
| 1 | 3 | -4 | -12 | 0 |
Yet another positive result, since the remainder of zero tells us that one is also one of the roots of our polynomial. This also means that there will be a second positive rational root, so we will try the next positive candidate, which is two:
| 2 | 1 | 2 | -7 | -8 | 12 |
| 2 | 8 | 2 | -12 | ||
| 1 | 4 | 1 | -6 | 0 |
So we have one final positive result that gives us our fourth rational root (two). We now have a full set of rational roots, which means we can rewrite the polynomial equation in factorised form as follows:
x4 + 2x3 - 7x 2 - 8x + 12 = 0 ⇒ (x + 2)(x + 3)(x - 1)(x - 2) = 0
Of course, not every polynomial equation will work out as conveniently as the previous example. Most will not, in fact. With high order polynomials, the aim should be to find as many factors as are required in order to reduce the problem to one of solving a second degree (i.e. quadratic) polynomial, since we can always use the quadratic formula, even if some or all of the roots are complex numbers. Finding just one root of a polynomial will reduce the overall complexity of our problem. Consider the following example:
x3 - 17x 2 + 54x - 8
The expression on the left-hand side of the equation is a third degree polynomial, so there will be three roots of one kind or another in total. The expression has three variations in sign, so according to the rule of signs, the number of positive roots will be either three or one. Looking at the function ƒ(-x), we can rewrite the expression as:
(-x)3 - 17(-x) 2 + 54(-x) - 8
Simplifying this gives us:
-x3 - 17x 2 - 54x - 8
For ƒ(x), there is no variation in sign, so according to the rule of signs there are no negative roots. The rational root test gives us candidate rational roots of (plus or minus) one, two, four and eight (±1, ±2, ±4 and ±8). Since we already know there are no negative roots, we can concentrate on the four positive candidates, the first of which is one:
| 1 | 1 | -17 | 54 | -8 |
| 1 | -16 | 38 | ||
| 1 | -16 | 38 | 30 |
Since we have a remainder, and since one of the numbers on the bottom row is negative, one is neither a rational root of our polynomial nor an upper bound for the real roots (we have already established that there will be either one or three positive real roots). Let's move on to the next candidate, which is two:
| 2 | 1 | -17 | 54 | -8 |
| 2 | -30 | 48 | ||
| 1 | -15 | 24 | 40 |
This is a similar result to the previous one. The remainder tells us that two is not one of the roots of our polynomial, and the negative value that appears on the bottom row means that two is not an upper bound for the real roots. Let's try the next candidate, four:
| 4 | 1 | -17 | 54 | -8 |
| 4 | -52 | 8 | ||
| 1 | -13 | 2 | 0 |
A positive result! The remainder of zero tells us that four is one of the roots of our polynomial, although the negative value on the bottom row also tells us it is not an upper bound, so there may be further real roots. Let's try the final candidate, which is eight:
| 8 | 1 | -17 | 54 | -8 |
| 8 | -72 | -144 | ||
| 1 | -9 | -18 | -152 |
So eight is not a rational root, but at least we have identified one rational root. We can now say with confidence that x3 - 17x 2 + 54x - 8 can be expressed as the product of (x - 4) and a second degree (quadratic) polynomial expression. We can use various means to find out a bit more about our missing quadratic expression. We can start by equating our third degree polynomial with the product of our newly discovered (linear) factor and the general form of the quadratic, as follows:
x3 - 17x 2 + 54x - 8 = (x - 4)(ax 2 + bx + c)
We need to find the values of a, b and c. We can start by multiplying out the brackets on the right:
x3 - 17x 2 + 54x - 8 = ax3 + bx 2 + cx - 4ax 2 - 4bx - 4c
Gathering like terms together we get:
x3 - 17x 2 + 54x - 8 = ax3 + (b - 4a)x 2 + (c - 4b)x - 4c
We can now use a process of equating coefficients to deduce the values of a, b and c. This means that we compare the coefficients of each term on the left-hand side of the equation with each corresponding term on the right-hand side. The coefficient of x3 on the left-hand side, for example, is one (if no coefficient explicitly appears in front of a variable, we can safely assume that the coefficient is one). This means that for the term ax3 on the right-hand side of the equation, the value of the coefficient a must also be one (1). We can apply the same principle to get the value of b by looking at the coefficient of x 2 on the left hand side which is minus seventeen (-17). We can therefore derive a value for b as follows:
b - 4a = -17 ⇒ b - 4 = -17 ⇒ b = -17 + 4 ⇒ b = -13
The coefficient of x on the left-hand side of the equation is fifty-four (54), so we can derive a value for c as follows:
c - 4b = 54 ⇒ c - (-52) = 54 ⇒ c + 52 = 54 ⇒ c = 2
Substituting values for a, b and c into the quadratic expression, we now get:
x3 - 17x 2 + 54x - 8 = (x - 4)(x 2 - 13x + 2)
A quick inspection shows that the quadratic expression cannot be factorised, although we had effectively already established that, and the graph of the third degree polynomial function y = ƒ(x) = x3 - 17x 2 + 54x - 8 appears to confirm that the remaining roots are non-rational (see below).
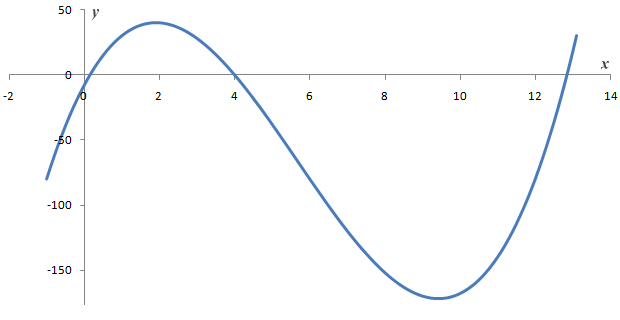
The graph of y = ƒ(x) = x3 - 17x 2 + 54x - 8
Our best option here is probably to use the quadratic formula to solve the quadratic equation and find the last two roots of our third degree polynomial. Applying the quadratic formula and plugging in the known values of a, b and c, we get:
| x = | -b ± √(b 2 - 4ac) |
| 2a |
| x = | -(-13) ± √((-13) 2 - 4(1)(2)) |
| 2(1) |
| x = | 13 ± √(169 - 8) |
| 2 |
| x ≈ | 13 ± 12.689 |
| 2 |
| x ≈ | 25.689 | or x ≈ | 0.311 |
| 2 | 2 |
| x ≈ 12.844 or x ≈ 0.156 |
Note that the discriminant (that's the expression under the radic or square root symbol) tells us what kind of roots we can expect. If the discriminant evaluates to a positive value, there will be two real roots. If the discriminant evaluates to zero, there will be a single real root (sometimes called a double root). If the discriminant evaluates to a negative number, there will be two complex roots.
Even ignoring the multivariate forms of polynomials, when we talk about polynomial equations we are talking about a very large family of equations indeed. As we have seen from the foregoing discussion and worked examples, second degree polynomials do not really present a problem because we have various tried and tested (and relatively straightforward) methods for solving them. Indeed, we have formulae that work for third and fourth degree polynomials, albeit of a complexity that means they are not really suitable for use in solving problems by hand.
If by factorising a high-order polynomial we can reduce it to the product of first and second degree (i.e. linear and quadratic) polynomial expressions, we are pretty much home and dry. We have looked at some of the methods that can be used to find suitable factors. Sometimes these methods can't help us, although there are various numerical methods (not covered here) that can be used to obtain approximate values for x that will satisfy a high order polynomial. We have also seen that we can graph the function corresponding to a particular polynomial equation to find the approximate location of the x-intercepts (if any), which will at least give us some idea of what kind of roots an equation has, and where they lie. In fact, the only limitation to using this method is the accuracy with which you can draw and interpret the graph.
This page is not intended to provide a panacea for solving all of the polynomial equations you are ever likely to encounter. Hopefully however, it has given you some insight into the nature of the problems you may face, and provided an introduction to a few of the methods that can be applied to solving them.