| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
"We have a society that is founded on science, but educationally we provide a university system that offers far more scope for studying the media than for studying physics." These words were spoken by MP Tony McWalter, in a Commons debate on the subject of quadratic equations that took place on June 26th 2003. Those interested in the content of this debate can find the relevant Hansard pages at the link below (for those that don't know, Hansard is the name given to the archived transcripts of parliamentary debates).
http://www.publications.parliament.uk/pa/cm200203/cmhansrd/vo030626/debtext/30626-21.htm
The debate was motioned in response to a suggestion by the president of the National Association of Schoolmasters Union of Women Teachers, in a televised interview that was part of a BBC Today program aired in April 2003, that mathematics should be dropped from the school curriculum as a compulsory subject at the age of fourteen. Mr. Bladen said during the interview:
For a significant number of pupils things like quadratic equations have absolutely no relevance to them, they can't see how they would ever use them and in fact they probably never would use them.
Mr. McWalter was moved to propose the debate as much by the lack of a government rebuttal to this statement as by the statement itself. Like most children, I was not overly fond of the quadratic equation (or mathematics in general) when I was at school. Nevertheless, to dismiss the quadratic equation as being irrelevant to any sector of society, especially when it comes from someone in such an elevated position in the educational world (and a former teacher of mathematics to boot!), suggests a profound lack of understanding of how important the quadratic equation (and of course mathematics in general) is to our modern society. In short, whether one appreciates the fact or not, civilisation as we know it would simply not exist if we had no understanding of the quadratic equation.
Whether your future career ambitions are centred on a job in science, telecommunications, or business, you cannot entirely avoid quadratic equations in the course of your studies. Quadratic equations have been used in one form or another for at least four thousand years, and their origins can be traced back to the ancient Babylonian civilisation where they were used for (among other things) calculating taxes. Quadratic equations are used to describe such diverse things as the orbits of the planets around the sun, the trajectory of an artillery shell, or the stopping distance of a motor vehicle travelling at a certain speed. They lie at the heart of many modern technological wonders that most of us take for granted but would sorely miss if we had to forego them, such as satellite TV and the mobile phone.
In fact, some of the greatest scientific discoveries made throughout history would not have been possible without an understanding of quadratic equations. Furthermore, much of the critical technology we rely on in our daily lives would simply not exist. And of course the other really good thing about the quadratic equation is that, like many things in life, once you become familiar with the basic principles it is really not so bad. So, even though some of us can probably get through life without using quadratic equations, it would seem like a good idea to at least have a working knowledge of what they are, what they might be used for, and how they work. So what is a quadratic equation used for? Here are just a few examples:
So what is a quadratic equation? A quadratic equation is a second order polynomial equation, i.e. a polynomial equation in which the highest order term has an exponent of two (2). The general form of a quadratic equation is:
ax 2 + bx + c = 0
There is a single variable (x) in the equation, with a, b and c representing constants. The constant a is called the quadratic coefficient, and is not allowed to be zero (otherwise, the equation simply reduces to a linear equation). The constant b is called the linear coefficient, and the constant c is called the constant term (or free term). One of the interesting things about quadratic equations is that they can have two solutions. This is because, providing the term ax 2 is positive, it can have two roots, either of which can be positive or negative (a negative value of x 2 would cause a problem, since negative numbers cannot have a square root, but we will deal with that subject elsewhere). Because the value (or values) of x will obviously be the root (or roots) of x 2, we sometimes refer to the solution(s) of a quadratic equation as the root(s) of the equation. We will be looking at various ways of solving quadratic equations in this section, but it is worth first considering the possible outcomes. This can be visualised by looking at the graph of a typical quadratic function. Here is the graph of the function y = ƒ(x) = x 2 - 4x - 5:
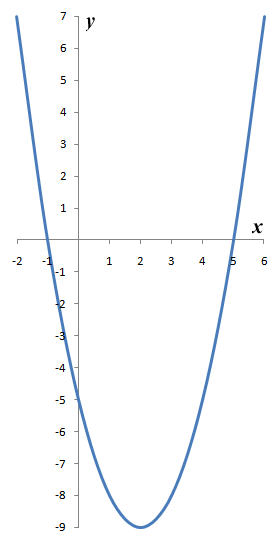
The graph of y = ƒ(x) = x 2 - 4x - 5 has two roots
We would write the corresponding quadratic equation as x 2 - 4x - 5 = 0. The solutions to this equation (i.e. the roots of the equation) are the values of x for which y is equal to zero. From the graph, we can see that there are two values of x (minus one and five) for which y is equal to zero. These are the values of x at which the graph intersects the x-axis. If we have a situation in which the graph does not intersect the x-axis, then the equation has no solutions. If the graph touches the x-axis at a single point, then the equation has a single solution (sometimes this is known as a double root). These scenarios are illustrated below.
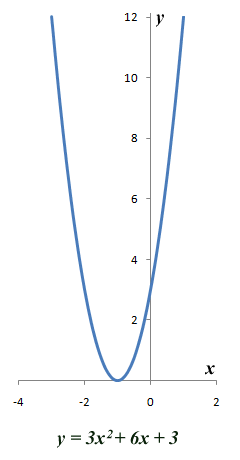
The quadratic equation 3x 2 + 6x + 3 = 0 has one solution (x = -1)
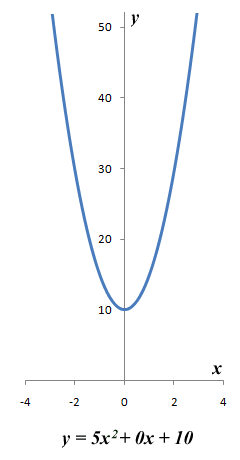
The quadratic equation 5x 2 + 0x + 10 = 0 has no solution