| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
We know that we can find the derivative of a non-linear function for some value of the independent variable x using the delta method of differentiation. This method works, but requires an algebraic approach that involves quite a lot of work. Fortunately, there are some basic rules that allow us to differentiate non-linear functions much more easily, once we have learnt how to apply them. Applying these rules to a non-linear function produces a formula into which we can plug any value of x for which we want to find the derivative.
Before we start looking at the rules, we should say something about notation. Something that often confuses students when they first encounter calculus is the use of different forms of notation to represent the same thing. You should bear this in mind when studying texts or online material dealing with differential calculus. The notation we will be using here is essentially that developed by the German mathematician and philosopher Gottfried Wilhelm Liebniz (1646-1716). For some function ƒ(x), we express the derivative of the function as:
| dy | = | d | (ƒ(x)) |
| dx | dx |
For example, if we take the function ƒ(x) = x2, we could express the derivative as:
| dy | = | d | (x2) = 2x |
| dx | dx |
Alternatively, we could just write:
| d | (x2) = 2x |
| dx |
The other form of notation you are likely to encounter for the derivative of a function is that developed by the Italian mathematician and astronomer Joseph-Louis Lagrange (1736-1813). This notation uses the function symbol (ƒ) together with the prime symbol (′) to denote the derivative of a function. The derivative of the function ƒ(x) = x2 would be written as:
ƒ′(x2) = 2x
The power rule (or polynomial rule or elementary power rule) is perhaps the most important rule of differentiation. It allows us to differentiate a term of the form xn, where x is the independent variable and n is the exponent (the power to which x is raised). The rule requires us to decrement the exponent by one and then multiply the term by n. We can express this formally as:
| d | (xn) | = nxn-1 |
| dx |
Let's look at a couple of examples to see how this works.
| d | (x2) | = 2x |
| dx |
| d | (x3) | = 3x2 |
| dx |
That was easy, wasn't it? Admittedly we used examples in which n is a positive integer, but things are just as straightforward if n is negative. Consider the following examples:
| d | (x-1) | = -x-2 |
| dx |
| d | (-x3) | = -3x2 |
| dx |
| d | (-x-1) | = x-2 |
| dx |
Supposing we must differentiate the function ƒ(x) = 1/x? Can we apply the power rule here? The answer is yes, but we must rewrite 1/x so that it becomes x raised to a power. There is a basic algebraic relationship you should be familiar with here, which is:
| 1 | = x-n |
| xn |
In the term 1/x the exponent of x is one, so we have:
| 1 | = x-1 |
| x |
We can now obtain the derivative:
| d | (x-1) | = -x-2 |
| dx |
We can apply the same principle to differentiate the function ƒ(x) = 1/x2. First we rewrite 1/x2 so that it becomes x raised to a power:
| 1 | = x-2 |
| x2 |
Then we find the derivative:
| d | (x-2) | = -2x-3 |
| dx |
We can do the same thing with functions that involve roots. Suppose we want to differentiate the function ƒ(x) = √x. This is not a problem, since we can express the nth root of x as a power using the following formula:
n√x = x1/n
This allows us to find the derivative of √x:
| d | (√x) = | d | (x1/2) = | 1 | x-1/2 = | 1 | · | 1 | = | 1 |
| dx | dx | 2 | 2 | √x | 2(√x) |
Let's look at one more example. We will differentiate the function ƒ(x) = 3√x:
| d | ( 3√x) = | d | (x1/3) = | 1 | x-2/3 = | 1 | · | 1 | = | 1 |
| dx | dx | 3 | 3 | x 2/3 | 3(x 2/3 ) |
As you can see, the power rule is fairly versatile. In addition to differentiating powers of x, we can also use it to differentiate terms that are reciprocals or roots, providing we can express these terms as some power of x. This does of course require a reasonable grasp of algebra, but that is a prerequisite for studying calculus.
A constant term in a function makes no difference to the shape of the function's graph. The graphs of the non-linear functions ƒ(x) = x3 - 2x and ƒ(x) = x3 - 2x + 3 are shown below. You can see that the addition of a constant term shifts the position of the graph vertically, but does not alter the shape of the graph. To emphasise the point, we have included the tangents to the graphs at points P and P', both of which have an x coordinate of one. As you can see, the tangents are parallel - they both have the same slope.
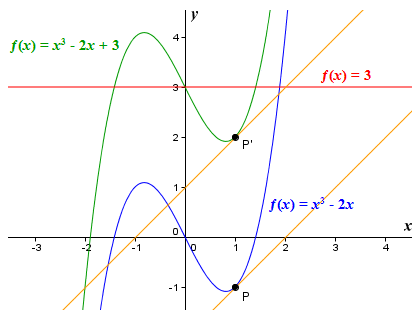
A constant term does not affect the shape of the graph
The graph of ƒ(x) = 3 is included here to illustrate the fact that the graph of any function ƒ(x) = c where c is a constant will be a horizontal line. The derivative of a constant term is therefore zero, and we can effectively ignore it. We can express this formally as:
| d | (c) = 0 |
| dx |
The derivatives of the functions ƒ(x) = x3 - 2x and ƒ(x) = x3 - 2x + 3 are therefore identical:
| d | (x3 - 2x) = 3x2 - 2 |
| dx |
| d | (x3 - 2x + 3) = 3x2 - 2 |
| dx |
One word of caution when differentiating functions. Suppose you are asked to find the derivative of the function ƒ(x) = π ln(5 + √2). At first glance this might look a little daunting, but the derivative is actually zero:
| d | (π ln(5 + √2)) = 0 |
| dx |
If you look again at the expression π ln(5 + √2) you will realise that it evaluates to a constant value of approximately five-point-eight-four (5.84). It is just pi multiplied by the natural logarithm of five plus the square root of two. Even if you encounter a term such as π3, the derivative will still be zero and not 3π2, because pi is a constant and not a variable. It is not always immediately obvious that an expression is in fact a constant, but you should take the time to check - it could save you a lot of unnecessary effort.
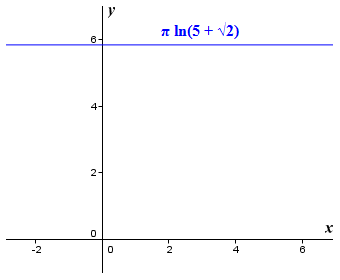
The graph of the constant function ƒ(x) = π ln(5 + √2)
The constant coefficient rule is sometimes called the constant multiple rule. It essentially states that the derivative of c·ƒ(x), where ƒ(x) is some function and c represents a constant coefficient, is equal to the derivative of ƒ(x) multiplied by c. We can express this formally as follows:
| d | (c · ƒ(x)) = c · | d | (ƒ(x)) |
| dx | dx |
The constant coefficient rule essentially allows us to ignore the coefficient in an expression while we differentiate the rest of the expression. Suppose we have a function ƒ(x) = 3x2. The constant coefficient rule tells us that the derivative of this function is equal to the derivative of x2 multiplied by three. In other words:
| d | (3x2) = 3 · | d | (x2) = 3(2x) = 6x |
| dx | dx |
For any function of the form ƒ(x) = cxn where c is a constant coefficient, we can express the derivative as follows:
| d | (cxn) = cnxn-1 |
| dx |
Let's look at another example. Applying the constant coefficient rule to the function ƒ(x) = 4x we get:
| d | (4x) = 4 · | d | (x) = 4(1) = 4 |
| dx | dx |
For the function ƒ(x) = x, both the coefficient and the exponent of x will be one, so using the power rule to find the differential of x gives us one multiplied by x to the power zero (x0). Since anything to the power of zero is one, the derivative will also be one. For any function of the form ƒ(x) = cx where c is a constant coefficient, we can express the derivative as follows:
| d | (cx) = c |
| dx |
A function may consist of a single term, or it may be a polynomial function - i.e. a function that consists of the sum (or difference) of several terms. The additive rule (sometimes called the sum rule) essentially tells us that, for a polynomial function, we must differentiate each term separately. The plus or minus sign in front of each term does not change. Consider the following function:
ƒ(x) = 2x3 + 3x2 - x + 7
Applying the additive rule we get:
| d | (2x3 + 3x2 - x + 7) = 6x2 + 6x - 1 |
| dx |
We use the power rule for each of the first three terms and the constant rule for the final term. We can apply the additive rule regardless of the sign in front of each term. Just think of a polynomial function as the sum of all its positive and negative terms. Note that we can also apply the additive rule to sum or difference of separate functions. Suppose we want to find the derivative of the sum of the functions ƒ(x) and g(x). We can express this formally as:
| d | (ƒ(x) + g(x)) = | d | (ƒ(x)) + | d | (g(x)) |
| dx | dx | dx |
Finding the derivative of the difference of these two functions works the same way:
| d | (ƒ(x) - g(x)) = | d | (ƒ(x)) - | d | (g(x)) |
| dx | dx | dx |
This is actually not so strange if you consider that each term in a polynomial function can be regarded as a function in its own right - even a term that consists of a constant value. Thus, when we differentiate a polynomial function, we are effectively differentiating the sum of two or more separate functions.