| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The intermediate value theorem is often associated with the Bohemian mathematician Bernard Bolzano (1781-1848). Much of Bolzano's work involved the analysis of functions, and is thought to have been inspired by the work of the Italian mathematician and astronomer Joseph-Louis Lagrange (1736-1813). Bolzano appears to have been the first mathematician to prove that the theorem worked for all continuous functions, although the Flemish mathematician and military engineer Simon Stevin (1548-1620) had provided proof nearly two centuries earlier that the theorem worked for polynomial functions. The French mathematician Augustin-Louis Cauchy (1789-1857) later provided his own proof of the theorem in his Cours d'Analyse, a celebrated text book on infinitesimal calculus published in 1821.
The intermediate value theorem essentially makes a statement about a function that is continuous over some defined interval. Remember that if a function is continuous, it has no gaps or breaks. In other words, you can draw a graph of the function by hand without taking your pencil off the paper. Suppose we have a function ƒ(x) that is continuous on some interval [a, b]. The function will take the value ƒ(a) at one end of the interval, and ƒ(b) at the other end of the interval. The intermediate value theorem states that the function must take every value between ƒ(a) and ƒ(b) at least once somewhere within the interval. The principle is illustrated below.
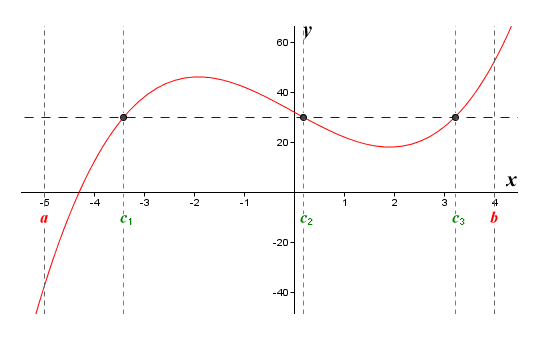
The graph of the function ƒ(x) = x 3 - 11x + 32
The illustration shows the graph of the function ƒ(x) = x 3 - 11x - 32 defined on the interval [a, b], where a is equal to minus five (-5), and b is equal to four (4). The value of the function at a will be:
ƒ(a) = a 3 - 11a + 32 = -125 + 55 + 32 = -38
and the value of the function at b will be:
ƒ(b) = b 3 - 11b + 32 = 64 - 44 + 32 = 52
According to the intermediate value theorem, the function must take every value between minus thirty-eight (-38) and fifty two (52) at least once somewhere within the interval [a, b]. To demonstrate the principle, we have taken an arbitrary value of thirty (30), which fits the requirement of being between minus thirty-eight and fifty two. According to the intermediate value theorem, there must be at least one value c between a and b for which the function will return the value thirty. In other words:
ƒ(c) = 30
Another way of thinking about this is that if we draw the horizontal line that represents the constant function y = 30, the line must intercept the graph of the function ƒ(x) = x 3 - 11x + 32 at least once within the interval [a, b]. In fact, as you can see from the illustration, there are three values between a and b (we have labelled these c1, c2 and c3) for which the function will return a value of thirty. You can clearly see that the dashed line representing the constant function y = 30 intercepts the graph at these three points.
The intermediate value theorem essentially just tells us something that we can grasp intuitively by looking at the graph of any continuous function defined on an interval [a, b], which is that the function will return every value between ƒ(a) and ƒ(b) at least once. What the theorem doesn't tell us is where a particular value will occur, or how many times that value will occur - just that it will occur somewhere within the interval. In addition, the theorem cannot tell us that a function does not take a particular value at some point within the interval - it can only tell us that a value definitely is taken by the function.
Although Bolzano is credited with providing the first proof of the intermediate value theorem, he was primarily interested in a special case of the theorem that could be used to determine that, at some point, the function would take the value zero (0). This special case of the intermediate value became known as Bolzano's theorem. We are still dealing with a function ƒ(x) that is continuous on some interval [a, b], for which the function takes the value ƒ(a) at one end of the interval, and ƒ(b) at the other end of the interval. This time, however, the values of ƒ(a) and ƒ(b) must be of opposite signs. That being the case, Bolzano's theorem states that the function must take a value of zero at least once somewhere within the interval. The principle is illustrated below.
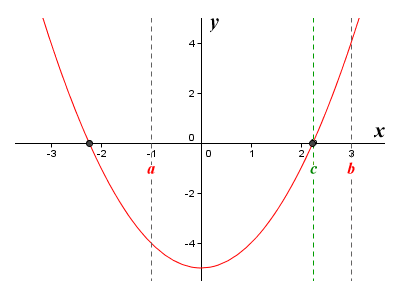
The graph of the function ƒ(x) = x 2 - 5
The illustration shows the graph of the function ƒ(x) = x 2 - 5 defined on the interval [a, b], where a is equal to minus one (-1), and b is equal to three (3). The value of the function at a will be:
ƒ(a) = a 2 - 5 = 1 - 5 = -4
and the value of the function at b will be:
ƒ(b) = b 2 - 5 = 9 - 5 = 4
According to the Bolzano's theorem, since the values of ƒ(a) and ƒ(b) satisfy the requirement that they must be of opposite signs, the function must take a value of zero at least once somewhere within the interval [a, b]. There must therefore be at least one value c between a and b for which the function will return the value zero. In other words:
ƒ(c) = 0
You can see from the illustration that such a value does indeed exist. As with the intermediate value theorem, however, Bolzano's theorem does not tell us anything else, such as where the value occurs, or how many occurrences there might be. You may therefore be wondering just how useful the intermediate value theorem (of which Bolzano's theorem is just a special case, remember) really is. After all, it doesn't give us any concrete results, in the form of actual numbers. There are however various ways in which the intermediate value theorem can be usefully applied. For example, we can use it to confirm that a continuous function has at least one real root. We can even use it as part of a somewhat rough and ready method of finding the real roots of a continuous function.
A real root of a function is a value of x for which the function takes the value zero (0). You can of course determine whether a function has any real roots and find approximate locations for them if they do exist by drawing the graph of the function. The real roots will be the values of x at which the curve intersects or touches the x axis. At the moment, however, we are more interested in how we can apply the intermediate value theorem to verify the existence of or locate the real roots of a continuous function. We will use polynomial functions for this purpose, because all polynomial functions are continuous. What else do we know about polynomial functions? Well, you might remember that the number of roots of a polynomial is never more than its degree, and that every polynomial of odd degree will have at least one real root. That knowledge can help us to narrow the search.
Supposing we have the function ƒ(x) = 2x 3 - 5x 2 - 10x + 5, defined on the interval [-1, 2]. We know that the function will be continuous on the interval because it is a polynomial function. And, because it is a third degree polynomial, we know that it could have up to three real roots. The question is, does the interval [-1, 2] contain a real root? In other words, does the function take the value zero somewhere within the interval? If we compute the values taken by the function at each end of the interval we get the following:
ƒ(-1) = (2)(-1) 3 - (5)(-1) 2 - (10)(-1) + 5 = -2 - 5 + 10 + 5 = 8
and
ƒ(2) = (2)(2) 3 - (5)(2) 2 - (10)(2) + 5 = 16 - 20 - 20 + 5 = -19
Remember that the intermediate value theorem tells us that a function ƒ(x) that is continuous on some interval [a, b] must take every value between ƒ(a) and ƒ(b) at least once somewhere within the interval. The function ƒ(x) = 2x3 - 5x2 - 10x + 5, defined on the interval [-1, 2], must therefore take every value between eight (8) and minus nineteen (-19), which will of course include the value zero. Consequently, we can say with absolute certainty that the function has at least one real root within the defined interval. The graph of the function is shown below, and confirms this conclusion.
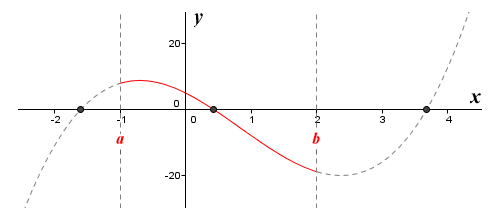
The graph of the function ƒ(x) = 2x 3 - 5x 2 - 10x + 5
You may already have realised that there is a potential problem with using the intermediate value theorem to confirm the presence of a real root of a function. It is perfectly possible, for example, to define a polynomial function on an interval for which real roots exist, but for which applying the intermediate value theorem (by calculating the function values at the endpoints) does not confirm this fact. Consider the illustration below, which once again shows the function ƒ(x) = 2x 3 - 5x 2 - 10x + 5, this time defined on the interval [-1, 4].
![The graph of the function f(x) = 2x^3 - 5x^2 - 10x + 5 defined on the interval [-1, 4]](images/differential_calculus_0043.gif)
The graph of the function ƒ(x) = 2x 3 - 5x 2 - 10x + 5 defined on the interval [-1, 4]
We have already established that the function will be continuous on the interval because it is a polynomial function. We can see from the illustration above that the graph of the function on the interval [-1, 4] intersects the x axis twice, which means that the function takes the value zero twice within the interval. The interval therefore contains not just one, but two real roots for the function ƒ(x) = 2x 3 - 5x 2 - 10x + 5. However, if we compute the values taken by the function at each end of the interval we get the following:
ƒ(-1) = (2)(-1)3 - (5)(-1)2 - (10)(-1) + 5 = -2 - 5 + 10 + 5 = 8
and
ƒ(4) = (2)(4)3 - (5)(4)2 - (10)(4) + 5 = 128 - 80 - 40 + 5 = 13
The intermediate value theorem tells us that the function must take every value between ƒ(a) and ƒ(b) at least once somewhere within the interval. It must therefore take every value between eight (8) and thirteen (13). Unfortunately, this range of values does not include zero. So, even though we know from looking at the graph of the function that it has two real roots on the interval defined, we cannot use the intermediate value theorem to verify this fact.
Clearly, there are some constraints we need to be aware of. If we want to use the intermediate value theorem to prove the existence of a real root of a function on an interval, we must choose suitable endpoints for the interval. An interval that contains an even number of real roots, for example, will always have end points for which the function values will have the same sign (i.e. both positive or both negative). If so, using the intermediate value theorem will not enable us verify the presence of real roots within the interval.
We said earlier that we can use our knowledge of the intermediate value theorem to locate the real roots of a continuous function. The method we use is essentially one that involves a fair amount of trial and error, and is called the bisection method. Let's consider the polynomial function ƒ(x) = x 3 - x + 1, defined on the interval [-2, 2]. We know that the function is continuous, because it is a polynomial function. If we compute the values taken by the function at each end of the interval we get the following:
ƒ(-2) = (-2) 3 - (-2) + 1 = -8 + 2 + 1 = -5
and
ƒ(2) = (2) 3 - (2) + 1 = 8 - 2 + 1 = 7
The intermediate value theorem tells us that the function must take every value between minus five (-5) and seven (7), which will include zero. We can therefore say for certain that the function has a real root within the interval [-2, 2]. Let's see what happens if we bisect the interval. This essentially means that we are going to calculate the value taken by the function at x = 0 (the midpoint of the interval [-2, 2]):
ƒ(0) = (0) 3 - (0) + 1 = 0 + 0 + 1 = 1
Applying the intermediate value theorem to the interval [-2, 0], we can see that the function does have a root in this interval, since it must take every value between minus five (-5) and one (1), and this range of values will include zero. For the interval [0, 2], we cannot conclude that there is a real root in this interval, because the function will take positive values at both ends of the interval (on the other hand, we cannot say for certain that there is not a real root in the interval [0, 2]). Now let's bisect the interval [-2, 0] by finding the value taken by the function at x = -1 (the midpoint of the interval [-2, 0]):
ƒ(-1) = (-1) 3 - (-1) + 1 = -1 + 1 + 1 = 1
Once again, if we apply the intermediate value theorem to the interval [-2, -1], we can see that the function must have a root in this interval, since it must take every value between minus five (-5) and one (1), and this range of values will include zero. You should by now be able to see how the process of bisection can be repeated as often as necessary in order to obtain a good approximation for the location of a real root. The bisection method works, but it is a somewhat cumbersome way of finding the real roots of a function. Needless to say, there are more efficient methods available. The graph of the function ƒ(x) = x 3 - x + 1 is shown below. You can see from the graph that the function only has one real root. As our application of the bisection method has already shown us, this root is located within each of the (successively smaller) intervals [-2, 2], [-2, 0], and [-2, -1].
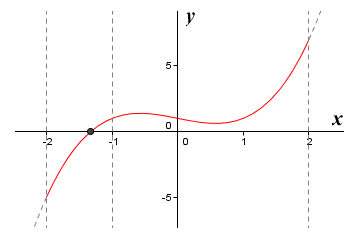
The graph of the function ƒ(x) = x 3 - x + 1