| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The law of cosines, sometimes called the cosine rule, is an equation that allows us to find the unknown length of one side of a triangle, providing the lengths of the other two sides and the size of the included angle are known. It also allows us to calculate the angles of a triangle if the lengths of all three sides are known. An explicit statement of the law of cosines first appears in the work of the Persian mathematician and astronomer Jamshīd al-Kāshī early in the fifteenth century CE. The geometric equivalent of the law of cosines goes back somewhat further however, to the work of the Greek mathematician Euclid. In his work the Elements, believed to have been written during the third century BCE, Euclid essentially extended Pythagoras' theorem to include triangles that were not right-angled triangles. Consider the triangle below.
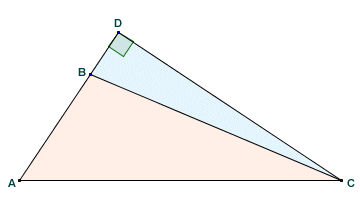
Triangle ABC is an oblique triangle
The triangle we are interested in here is triangle ABC, which is an oblique triangle (i.e. it is not a right-angled triangle). Angle ABC is in fact an obtuse angle (i.e. it is greater than ninety degrees). For right-angled triangle ACD, providing we know the length of two of the sides, we can apply Pythagoras' theorem to find the length of the third side:
AC 2 = AD 2 + CD 2
In Proposition 12 of Book II of the Elements, Euclid essentially said that in an oblique triangle containing an obtuse angle, the square of the longest side of the triangle (i.e. the side opposite the obtuse angle) is greater than the sum of the squares of the other two sides. The problem is to determine by how much. Euclid solved the problem by extending one of the shorter sides to create a right-angled triangle. In the diagram above, we have extended side AB to point D to create the right-angled triangle ACD. According to Euclid, if we take the area of a rectangle equal to AB · BD and double it, this gives us the difference in area that we are looking for. We can express this formally as:
AC 2 = AB 2 + BC 2 + 2 (AB · BD )
This does eventually make sense when you think about it. The diagram below should help to clarify matters. We know from Pythagoras' theorem that AC 2 is equal to the sum of AD 2 and CD 2. Applying Pythagoras' theorem to triangle BCD, you should be able to see that BC 2 is equal to BD 2 + CD 2, so squaring side BC has effectively given us a surplus equal to BD 2. Squaring side AB, on the other hand, leaves us with a deficit. In order to make up the total area of AD 2, we need to add the two rectangles shown, each of which has an area of AB · BD, plus a square with an area of BD 2, which we can "borrow" from BC 2 to balance things up.
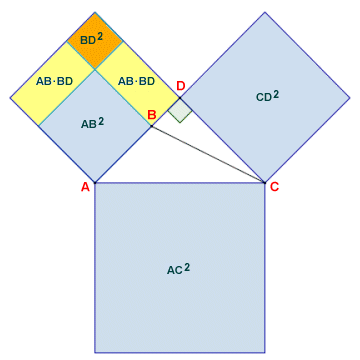
Euclid's Proposition 12, Book II
We can express all that a bit more formally as:
AC 2 = BC 2 - BD 2 + AB 2 + 2 (AB · BD ) + BD 2
Simplifying, we get:
AC 2 = BC 2 + AB 2 + 2 (AB · BD )
This is the same equation we saw earlier, apart from the fact that the terms are in a slightly different order. Euclid took a similar approach for oblique triangles in which all of the angles are acute (i.e. less than ninety degrees). He stated that the square of the side opposite one of the acute angles is less than the sum of the squares of the sides containing that angle. Again, the question is, by how much? Consider the diagram below, which represents Proposition 13 of Book II of the Elements.
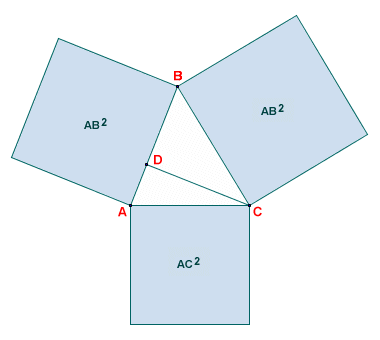
Euclid's Proposition 13, Book II
In this diagram we are again considering angle ABC, but this time the angle is acute. The side opposite angle ABC is side AC. Euclid's proposition involves drawing a line segment from either vertex A or vertex C to intersect one of the sides opposite the vertex (i.e. one of the sides containing angle ABC ) at right angles. In our example, we have drawn the line segment from vertex C to point D on side AB such that line segment CD is perpendicular to line segment AB. Euclid's proposition states that the sum of the squares of sides AB and AC is greater than the square of side BC by an amount equal to twice the area of the rectangle contained by side AB and line segment BD, which can be seen in the diagram below.
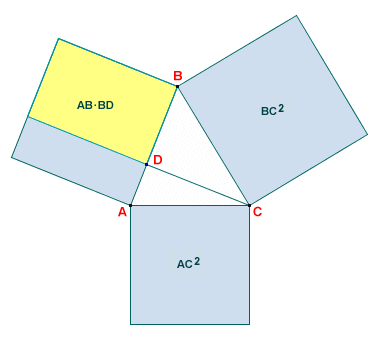
AC 2 = AB 2 + BC 2 - 2 (AB · BD )
For a triangle ABC in which all of the angles are acute, therefore, the geometric equivalent of the law of cosines, as described by Euclid, is very similar to that for a triangle containing an obtuse angle. The obvious difference is that line segment BD intersects side AB rather than extending it, and AC 2 is the result of subtracting twice the area of rectangle AB · BD from the sum of the square of the other two sides. Remember that for a triangle containing an obtuse angle, we had to add twice the area of rectangle AB · BD to the sum of the square of the other two sides in order to get AC 2. The equation for acute triangles is therefore:
AC 2 = AB 2 + BC 2 - 2 (AB · BD )
The law of cosines is another way of expressing this relationship between the sides of a triangle, and is therefore itself an extension of Pythagoras' theorem. The law of cosines, as its name suggests, uses the trigonometric cosine function to express the relationship. It is more powerful than its geometric equivalent because it allows us to find the size of missing angles, as well as the length of missing sides. The law of cosines can be stated algebraically as:
c 2 = a 2 + b 2 - 2ab · cos (C )
where a, b and c are the lengths of the sides of the triangle, and C is the angle opposite side c. We have assumed the conventional notation for labelling a triangle, so sides a and b are the sides opposite angles A and B respectively. You may have already deduced that the term ab · cos (C ) is equivalent to the area of rectangle AB · BD. Note that if angle C is obtuse (i.e. greater than ninety degrees), the cosine will be negative. We will therefore add twice this value to a2 + b2 to get c2. If angle C is acute (i.e. less than ninety degrees), the cosine will be positive. We will therefore subtract twice this value from a2 + b2 to get c2. Note that the equation for the law of cosines as expressed above will give us the square of side c. We can easily rearrange the equation in order to find the cosine of angle C:
| cos (C ) = | a2 + b2 - c2 |
| 2ab |
In the equations given above, we must assume that we are trying to find the length of side c or the size of angle C. However, the law of cosines can be applied in exactly the same formats to find the length of any side of a triangle, providing we know the lengths of the other two sides and the included angle, or the size of any angle provided we know the lengths of all three sides. Consider the triangle below, which we have labelled using conventional notation.
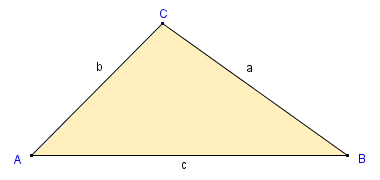
Conventional notation for labelling a triangle
We can solve for sides a, b or c of the triangle using one of the following equations:
a2 = b2 + c2 - 2bc · cos (A )
b2 = a2 + c2 - 2ac · cos (B )
c2 = a2 + b2 - 2ab · cos (C )
Similarly, we can solve for angles A, B or C using one of the following equations:
| cos (A ) = | b2 + c2 - a2 |
| 2bc |
| cos (B ) = | a2 + c2 - b2 |
| 2ac |
| cos (C ) = | a2 + b2 - c2 |
| 2ab |
As we have said, if we know the lengths of two of the sides of a triangle and the size of the included angle, we can find the length of the third side using the law of cosines. Let's look at a couple of examples. Consider the triangle below.
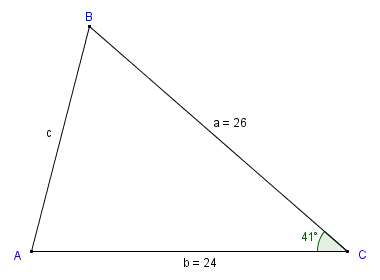
We want to find the length of side c
In the triangle above, we are given the length of sides a and b and the size of angle B (the included angle). Let's apply the law of cosines to the problem in the appropriate format:
c2 = a2 + b2 - 2ab · cos (C )
Substituting actual values, we get:
c2 = 676 + 576 - (1248 · cos (41)) = 1252 - (1248 × 0.755) = 309.76
c = √309.76 = 17.6
Now consider the triangle below.
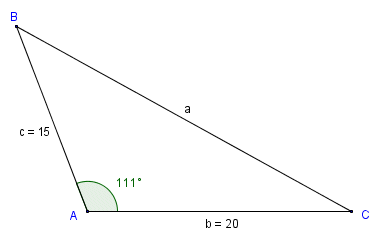
We want to find the length of side a
In the triangle above, we are given the length of sides b and c and the size of angle A (the included angle). Let's apply the law of cosines to the problem once more in the appropriate format:
a2 = b2 + c2 - 2bc · cos (A )
Substituting actual values, we get:
a2 = 400 + 225 - (600 · cos (111)) = 625 - (600 × -0.358) = 309.76
a = √839.8 = 28.98
Note that this time, because angle A is obtuse (i.e. greater than ninety degrees) the value of the cosine is negative. We therefore have to add the value of 2bc · cos (A ) to the sum of b2 and c2 to get a2.
As we said earlier, we can also use the law of cosines find any angle in a triangle if we know the length of all of the sides. Obviously, once we have found two of the angles, finding the size of the third angle is a trivial exercise, since the internal angles of a triangle must always sum to one hundred and eighty degrees. Consider the diagram below.
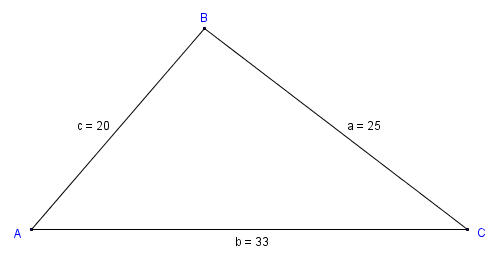
We want to find the size of angles A, B and C
Let's start by finding angle A. We'll use the law of cosine equations in the appropriate format for this type of problem, i.e. with the cosine of the angle we are trying to find on the left-hand side of the equation:
| cos (A ) = | b2 + c2 - a2 |
| 2bc |
Substituting actual values, we get:
| cos (A ) = | 1089 + 400 - 625 | = 0.655 |
| 1320 |
A = cos-1 (0.655) = 49.08°
Now we'll find angle B:
| cos (B ) = | a2 + c2 - b2 |
| 2ac |
Substituting actual values, we get:
| cos (B ) = | 625 + 400 - 1089 | = -0.064 |
| 1000 |
B = cos-1 (-0.064) = 93.67°
Finding the value of angle C is now a trivial exercise:
C = 180 - (49.08 + 93.67) = 37.25°
Note that the answers you get for these calculations may vary somewhat from those shown, depending on the number of decimal places used to record intermediate results. When performing calculations of this kind, it is a good idea to store intermediate results in their original format where possible, rather than using values that have been rounded up or down, particularly if the accuracy of the answer is critical.