| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
On this page we look at the last of the three main trigonometric functions (sine, cosine and tangent). The tangent function has a somewhat different history from the sine and cosine functions. Whereas the sine and cosine evolved from the need to make astronomical calculations, the tangent evolved more from things like the need to calculate the height of buildings. During the sixth century BCE, the Greek philosopher Thales is believed to have visited Egypt, where he learned of Egyptian methods for calculating heights and distances by measuring the lengths of shadows. He is said to have measured the height of a pyramid, for example, by measuring the length of the pyramid's shadow (measured from the centre of the pyramid) at the same time of day that the length of his own shadow was equal to his height.
The idea of using the length of shadows, both to obtain measurements of the height of physical objects and to mark time, had been used for thousands of years by the Egyptian and Babylonian civilisations. The instrument used to perform such measurements was called a shadow stick or gnomon, one form of which can still be seen as the upright component of a sundial. Thales recognised that, as the sun moves across the sky, the relationship between the length of an object's shadow and its height will be in the same proportion for all objects. However, the relationship between the height of an object, the length of the object's shadow, and the angle of elevation of the sun in the sky does not appear to have been expressed in terms of a trigonometric function until much later.
By the middle of the ninth century CE, Arab scholars had assimilated much of the astronomical and mathematical knowledge of the ancient world. They were familiar with all six trigonometric functions in modern use, and had compiled accurate trigonometric tables, including tables of tangents and cotangents, which they called tables of shadows. Indeed, the term tangent did not appear until towards the end of the sixteenth century CE, when it was used by the Danish mathematician and physicist Thomas Fincke, in his book Geometriae Rotundi. Prior to that, the tangent and cotangent had been known by their Latin names umbra recta and umbra versa, meaning straight shadow (the horizontal shadow cast by a vertical gnomon) and turned shadow (the vertical shadow cast by a gnomon attached to a wall) respectively.
The tangent function is related to the tangent line. A tangent line is a straight line that touches a curve at a single point. At the point where the tangent line touches the curve, we can say that the tangent line is "going in the same direction" as the curve at that point. More correctly, the tangent line has the same slope as the curve at the point of contact. The screenshot below shows the tangent line for the unit circle at the point where line segment OP intersects the circumference of the circle. Line segment OP is a radius of the circle, and also the hypotenuse of right-angled triangle OPE. Line segments EP and EO are the opposite and adjacent sides of the right-angled triangle in relation to angle θ. Since the unit circle has a diameter of one unit, the lengths of line segments EP and EO are also equal in value to the sine and cosine respectively.
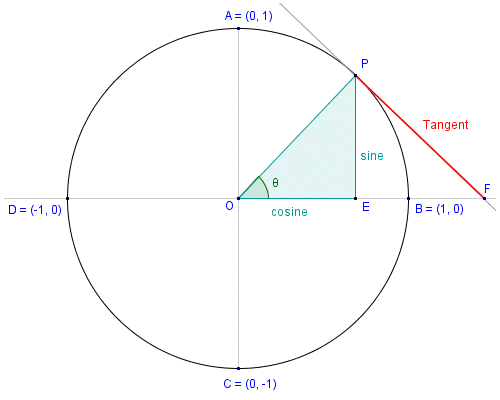
The tangent line touches the unit circle at point P
Note that the tangent line is perpendicular to the hypotenuse of the right angled triangle. The tangent function, like the sine and cosine functions, is the ratio of two sides of a right-angled triangle. It is also represented by a line segment associated with the unit circle. Unlike the sine and cosine however, the length of the line segment in question is not limited to values of between zero and one. As you can see from the illustration above, the tangent is represented by the line segment joining point P (the point on the circumference of the circle whose x and y coordinates represent the values of the cosine and sine respectively) and point F (the point where the tangent line intercepts the x-axis).
Click here to see an interactive demonstration that uses the unit circle to show how the sine, cosine and tangent relate to one another (note: your browser must support Java in order for the interactive page to work). You will see from the demonstration, if you have not deduced it already, that as the value of angle θ approaches ninety degrees (90°), the length of line segment PF will tend to infinity. You will also see that the same thing happens as the value of angle θ approaches two hundred and seventy degrees (270°). We will come back to the implications of this fact shortly. Meanwhile, consider the right-angled triangle illustrated below.
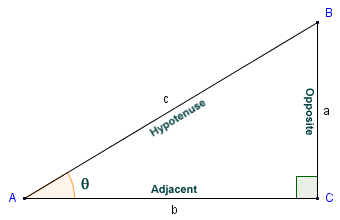
In triangle ABC, tan (θ ) = a/b
In triangle ABC, we are interested in angle θ. We have used the convention of labelling each vertex with an upper case character, and the side opposite each vertex with the corresponding lower-case character. The opposite in relation to angle θ is side a. The adjacent is side b, and the hypotenuse is side c. The tangent of an angle in a right-angled triangle is defined as the quotient of the lengths of the opposite and the adjacent. Thus, in triangle ABC, the tangent of angle θ is given as:
| tan (θ ) = | a |
| b |
If you have read the pages entitled "The Sine Function" and "The Cosine Function" (or maybe even if you haven't), you will be aware that the sides of a right angled triangle can be labelled in accordance with the way in which they relate to the acute angle in which we are interested, and the trick is to remember which of the sides to use in order to calculate the value of whatever trigonometric function we want to find. Here once again is the (relatively) easy-to-remember mnemonic SOH-CAH-TOA, which should remind you that:
Sine = Opposite over Hypotenuse
Cosine = Adjacent over Hypotenuse
Tangent = Opposite over Adjacent
Looking at the above definitions, and remembering that the hypotenuse is always the longest side in any right-angled triangle, it should be self-evident that the sine and cosine values for a right-angled triangle defined using Cartesian coordinates will always fall within the range minus one to one (-1 to 1). In fact, the sine and cosine values can be defined in terms of the y and x coordinates respectively of a point P on the circumference of the unit circle. The tangent, on the other hand, is defined as the quotient of those values:
| tan (θ ) = | y |
| x |
Since the coordinates y and x represent the sine and cosine respectively, we can also conclude that:
| tan (θ ) = | sin (θ ) |
| cos (θ ) |
Again, in terms of the unit circle, the hypotenuse of the right-angled triangle is the line segment connecting the centre of the circle to point P. If we consider the line segments representing the cosine and sine functions to be the run and rise respectively for the line segment connecting the centre of the circle and point P, then the value returned by the tangent function for angle θ represents the slope of the line segment (i.e. the slope of the hypotenuse). For those interested in such things, we have used Microsoft Excel to produce our own table of tangent values for angles ranging from zero degrees (0°) up to three hundred and sixty degrees (360°) in increments of one tenth of a degree. To see the table, click here.
If you study the table, you can see that there is a significant range of angles between zero and ninety degrees for which the value returned by the tangent function (i.e. the slope of the hypotenuse) changes only relatively slowly. As the size of angle θ approaches zero degrees (0°), the value returned by the tangent function tends to zero. Indeed, when angle θ reaches zero degrees, both the slope of the hypotenuse and the value of tan (θ ) will be zero. As the value of angle θ approaches ninety degrees (90°), however, the value returned by the tangent function tends rapidly to infinity. This is to be expected, since the value of cos (θ ) will tend to zero. In fact, the value returned by the tangent function for an angle of ninety degrees is considered to be undefined, since the equation tan (θ ) = sin (θ )/cos (θ ) will involve division by zero. The same is true for an angle of two hundred and seventy degrees (270°). In fact, it will apply to any angle for which the cosine value is zero. Similarly, whenever the value of sin (θ ) is zero, the value of tan(θ ) will also be zero. We present here the graph of the tangent function for angles of from zero to seven hundred and twenty degrees (720°):
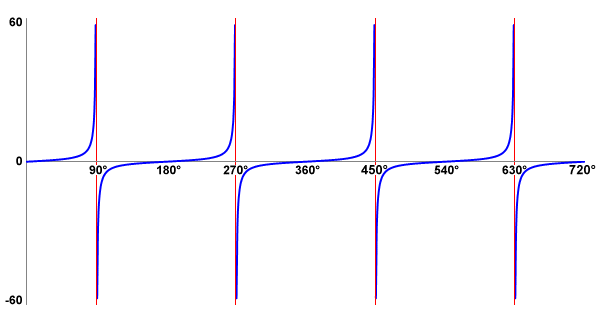
A graph of the tangent function for angles in the range 0° to 720°
The vertical red lines on the graph are asymptotes. The asymptote of a curve is a line such that as the distance between the curve and the line approaches zero, the value of the curve tends to infinity. In this case, the asymptotes can be considered to be the "gaps" in the graph where the value of tan (θ ) is undefined. Notice also that as the graph crosses the asymptote, the value of tan (θ ) goes from its maximum positive value to its maximum negative value. You can also see how the values differ on either side of the asymptote by studying the table of tangent values. One final thing to note here is that, like the sine and cosine functions, the tangent function is also periodic. Unlike the sine and cosine functions, however, the period of the tangent function is one hundred and eighty degrees (180°) rather than three hundred and sixty degrees (360°).
Fortunately, there is no longer any need to use tables or a slide rule to find the tangent of an angle (or the angle corresponding to a given tangent value), since any modern scientific calculator can do it for us. Finding the tangent of an angle with the built-in calculator provided in Microsoft Windows is relatively straightforward. Let's assume we want to find the tangent of an angle of thirty-five degrees (35°). You can find the Microsoft Windows built-in calculator by clicking on the start button in Windows 7 and selecting All Programs>Accessories>Calculator (other versions of Windows might require a different sequence of keystrokes). The scientific version of the calculator can be selected from the application's View menu. To find the tangent of thirty-five degrees using the Windows calculator, enter the following keystrokes (if you don't have the Windows calculator, use any available calculator that can perform trig functions):
Enter these keystrokes to find the tangent of 35°
Make sure, by the way, that you have the calculator set to the Degrees mode (unless you are planning to enter a value for the angle in radians or gradians). If you have entered the keystrokes correctly, you should now see the following display:
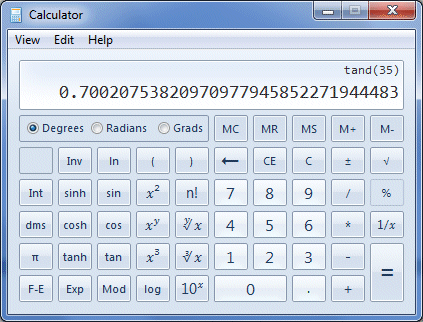
The calculator displays the value of tan (35° )
Let's assume that you want to find the size of an acute angle in a right-angled triangle by first finding the quotient of the opposite and adjacent (i.e. the angle's tangent). Providing you have values for the lengths of the sides of the triangle, you can find the value of the angle's tangent easily enough. Finding the angle is then simply a case of applying the arctangent function (which is the inverse of the tangent function) to the result. Let's find the value of angle θ for the right-angled triangle illustrated below.
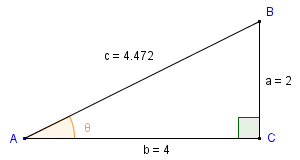
We want to find the size of angle θ
For angle θ, sides a and b are the opposite and the adjacent respectively. We can actually find the size of the angle in a single operation on the Windows calculator. We do this by using brackets in the key sequence entered, in order to get the calculator to find the quotient of the opposite and adjacent (i.e. the tangent of the angle) first. We then apply the arctangent function to the result. Here is the key sequence to use:
Enter these keystrokes to find the size of angle θ
If you have entered the keystrokes correctly, you should see the following display:
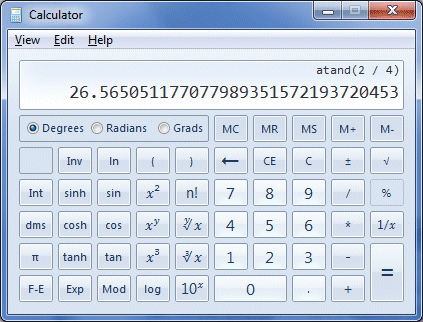
The calculator displays the value of angle θ
The three main trigonometric functions (sine, cosine and tangent) are usually studied in the order listed here. If you have read the pages in this section in order, you are now hopefully reasonably familiar with all three. At this point, therefore, it is probably worth looking at how the sign of the values returned by each of these trigonometric functions varies in relation to the quadrants of the unit circle. The illustration below should help to clarify matters.
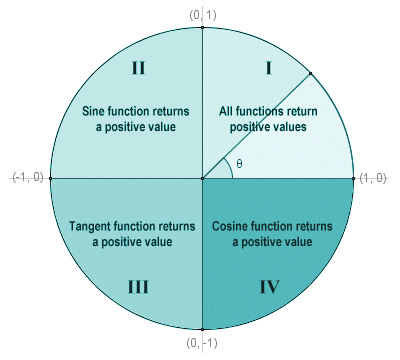
The quadrants of the unit circle
Remembering that the values returned by the cosine and sine functions will be equal to the x and y coordinates respectively of a point on the circumference of the circle, and that the value returned by the tangent function will be the quotient of the sine and cosine, then in Quadrant I, all three trigonometric functions will return positive values because x and y will both be positive. In Quadrant II, y is still positive but x will be negative, so only the sine function will return a positive value. In Quadrant III, both x and y are negative, so the sine and cosine functions will both return negative values. Only the tangent function (as the quotient of two negative values) will return a positive value. In Quadrant IV, x is positive but y is still negative, so the sine and tangent functions will return negative values and only the cosine function will return a positive value.
For completeness, it only remains to mention the fact that the tangent function, like the sine and cosine functions, can be represented as an infinite series. The value returned by a trigonometric function for a given angle cannot be calculated using a simple algebraic formula. For most angles, an exact value can only be obtained as the sum of an infinite number of terms, which is obviously impossible to achieve. A reasonably accurate approximation of the value is found using the sum of a limited number of terms from the function's infinite series. The greater the number of terms included, the greater the accuracy of the result. The number of terms used will depend on the accuracy required for a given application and on the computational resources available. The infinite series frequently given in trigonometry text books for the tangent function, for values of x (in radians) of less than π/2 (ninety degrees), looks like this:
| tan (x) = x + | 1 | x3 + | 2 | x5 + | 17 | x7 + | 62 | x9 + · · · |
| 3 | 15 | 315 | 2835 |