The Sine Function
The trigonometric sine function is closely related to the Greek chord function (if you are not familiar with the chord function, you may wish to read the page entitled "Chords"). In fact the sine function, sometimes known as the half-chord function, has the same relationship with the radius of a circle as the chord function has with the diameter of a circle. The first appearance of the sine function (as distinct from the chord function) appears in the Surya Siddhanta (the word Siddhanta means doctrine or tradition), sometimes described as a text book of Hindu Astronomy, and probably the best known of a number of Siddhantas. The exact origins of these writings are a matter for conjecture. The Surya Siddhanta is believed to have been influenced by the writings of Greek astronomers, Sanskrit translations of which were available in India by the third century CE, although it could be much older.
The properties of the sine (or half-cord) function were certainly known to the Indian mathematician and astronomer Aryabhata. His celebrated work, called the Aryabhativa, contained a collection of the teachings contained within the various Siddhantas. Written around the end of the fifth century CE, this work included a definition of the sine as the relationship between one half of a chord and one half of the central angle subtended by the chord. It also included tables of sine values from zero degrees (0°) up to ninety degrees (90°) in twenty-four increments of three and a quarter degrees (3.75°). They are believed to be the oldest surviving examples of sine tables, and are accurate to four decimal places. The relationship between the half-chord and the central angle θ that it subtends is illustrated below.
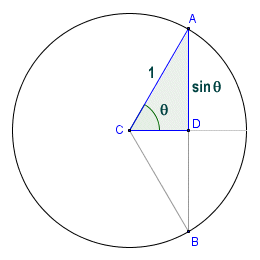
Angle θ is the central angle subtended by half-chord AD
As you can hopefully see from the diagram, the half-chord AD is one leg of right-angled triangle ADC. The other leg is line segment CD, which is the perpendicular bisector of chord AB. The hypotenuse AC of the right-angled triangle is a radius of the circle. We have used a unit circle here (i.e. a circle with a radius of one unit), which means that by definition, half-chord AD is equal to the sine of angle θ. For a circle of arbitrary radius r, the length of half-chord AD would be equal to sin (θ ) r. The relationship between the chord function and the sine function is given by the equation:
| crd (α) = 2 sin ( | α | ) = 2 sin (θ ) |
| 2 |
where α is the central angle subtended by the chord. Just as the chord function used by Greek astronomers and mathematicians is all about the properties of a right-angled triangle inscribed in a semi-circle, the sine function favoured by Indian scholars is all about the properties of a right-angled triangle in a quadrant.
Over the next few centuries, Indian scholars continued to develop their knowledge of trigonometry, compiling sine tables accurate to twelve decimal places. By the eighth century CE, however, much of the astronomical and mathematical knowledge of the Greeks, the Chinese, and the Indians had been translated into Arabic. Islamic scholars assimilated and extended this accumulated knowledge, and by the tenth century CE had established trigonometry as a branch of mathematics in its own right, and had produced comprehensive and accurate trigonometric tables, including tables of sine values. Although Islamic influence had begun to wane by the twelfth century CE, many of the writings of Islamic scholars had found their way to Europe, mainly via the Iberian peninsula which remained under Moorish rule until the fifteenth century CE.
The Sanskrit word for sine is jiya, which means bowstring. Arab scholars are thought to have used the word jiba, which is actually meaningless in Arabic, and then later translated (or possibly mistranslated) the word as jaib, which in Arabic means fold. European scholars translated the Arabic word into Latin as sinus (also meaning fold), from which we get the anglicised word sine. A more significant contribution of European scholars was to develop a representation of the sine function as the sum of an infinite number of terms (sometimes called an infinite series). Without going into too much detail here, we'll just consider one example of this kind of representation, which gives the sine of an angle x (expressed in radians) as:
| sin (x) = x - | x3 | + | x5 | - | x7 | + · · · |
| 3! | 5! | 7! |
Obviously, it is not practical, or even possible, to perform calculations using an infinite number of terms. The number of terms actually used will depend on the degree of accuracy required for the sine value.
Another development attributed to European scholars is the definition of trigonometric functions in terms of a right-angled triangle alone, rather than in terms of a right-angled triangle inscribed within a semi-circle or a quadrant. The way in which the sine function relates to the right angled triangle is illustrated below. In any right-angled triangle, one of the internal angles will always be ninety degrees (90°). Since the internal angles in any triangle must always sum to one hundred and eighty degrees (180°), the other two internal angles must both be acute angles (i.e. less than ninety degrees). The side opposite the right-angle is always the longest side, and is called the hypotenuse. In relation to either one of the acute angles, the side opposite the angle is referred to as the opposite. The remaining side (the side common to both the angle in which we are interested and the right angle) is called the adjacent.
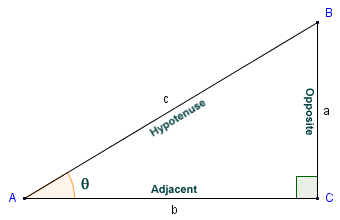
In triangle ABC, sin (θ ) = a/c
In triangle ABC, we are interested in angle θ. We have used the convention of labelling each vertex with an upper case character, and the side opposite each vertex with the corresponding lower-case character. The opposite in relation to angle θ is side a. The adjacent is side b, and the hypotenuse is side c. The sine of an angle in a right-angled triangle is defined as the quotient of the lengths of the opposite and the hypotenuse. Thus, in triangle ABC, the sine of angle θ is given as:
| sin (θ ) = | a |
| c |
In the illustration below, and using the same right-angled triangle, we show part of a circle with its centre at point A and a radius r = c. We have extended line segment BC to a point D on the perimeter of the circle, so that line segment BD becomes a chord of the circle. In relation to triangle ABC, side a (the opposite) becomes the half-cord subtending angle θ. Side b (the adjacent) becomes the chord's perpendicular bisector, and angle θ is half the central angle subtended by the chord. We include this diagram to emphasize the relationship between right-angled triangles and circles.
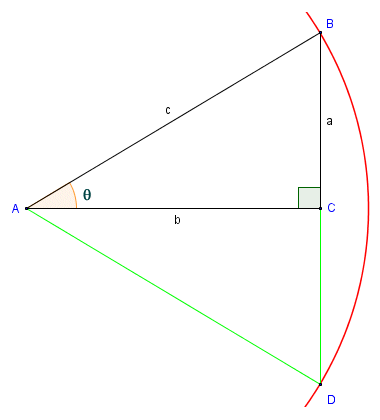
Angle θ is half of the central angle subtended by chord BD
Hopefully you can see that, despite trigonometry often being described as the branch of mathematics that studies the relationships between the sides and angles of triangles, it is also vitally important for the study of circles and cyclic phenomena. Note, by the way, that had we been interested in the sine of angle ABC, side b would have been the opposite and side a the adjacent. The circle would have been the same size (i.e. radius r = c), but this time point B would be the centre of the circle, and the circumference would pass through point A.
At this point, although we are at the moment really only interested in the sine function, it is worth mentioning that each of the three main trigonometric functions (sine, cosine and tangent) describes the ratio of two of the sides of a right-angled triangle with respect to one of its acute angles. The definitions of the sine, cosine and tangent functions with respect to right-angled triangles are very simple. The problem for many students of trigonometry seems to be in remembering which two sides of the right-angled triangle are used to calculate each of the trigonometric functions for the angle in question. English-speaking students often use the relatively easy-to-remember mnemonic SOH-CAH-TOA, which should remind them that:
Sine = Opposite over Hypotenuse
Cosine = Adjacent over Hypotenuse
Tangent = Opposite over Adjacent
Back in the days when I went to school we didn't have calculators. Finding the sine of an angle (or the angle corresponding to a given sine value) involved the use of trigonometric tables, and I have to confess that the use of such tables proved to be something for which I had absolutely no aptitude, although they seem perfectly straightforward to me now. I also vaguely remember a brief period during which I struggled to understand the mysteries of the slide rule, which allegedly made the use of trigonometric functions somewhat easier. Today, thankfully, we have sophisticated calculators that can instantly find the sine of an angle (or, conversely, the angle corresponding to a sine value) providing, of course, you know how to use the calculator. Using Microsoft Excel, we have produced own table of sines for angles ranging from zero degrees (0°) up to three hundred and sixty degrees (360°) in increments of one tenth of a degree. To see the table, click here.
Finding the sine of an angle with the built-in calculator provided in Microsoft Windows is relatively straightforward. Let's assume we want to find the sine of an angle of fifty degrees (50°). The screenshot below shows the scientific version of the Microsoft Windows built-in calculator. You can find this by clicking on the start button in Windows 7 and selecting All Programs>Accessories>Calculator (other versions of Windows might require a different sequence of keystrokes). The scientific version of the calculator can be selected from the application's View menu.
The Microsoft Windows built-in calculator
To find the sine of fifty degrees using the Windows calculator (if you have it, otherwise use whatever calculator you have available), enter the following keystrokes:
Enter these keystrokes to find the sine of fifty degrees
Make sure, by the way, that you have the calculator set to the Degrees mode (unless you are planning to enter a value for the angle in radians or gradians). If you have entered the keystrokes correctly, you should now see the following display:
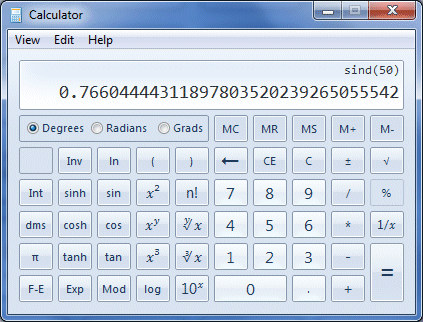
The calculator displays the value of sin (50°)
Let's assume that you want to find the size of an acute angle in a right-angled triangle by first finding the quotient of the opposite and hypotenuse (i.e. the angle's sine). Providing you have values for the lengths of the sides of the triangle, you can find the value of the angle's sine easily enough. Finding the angle is then simply a case of applying the arcsine function (which is the inverse of the sine function) to the result. Let's find the value of angle θ for the right-angled triangle illustrated below.
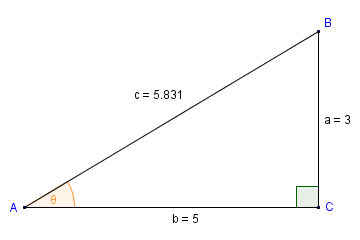
We want to find the size of angle θ
For angle θ, sides a and c are the opposite and the hypotenuse respectively. We can actually find the size of the angle in a single operation on the Windows calculator. We do this by using brackets in the key sequence entered, in order to get the calculator to find the quotient of the opposite and hypotenuse (i.e. the sine of the angle) first. We then apply the arcsine function (which is the inverse of the sine function) to the result. Here is the key sequence to use:
Enter these keystrokes to find the size of angle θ
If you have entered the keystrokes correctly, you should see the following display:
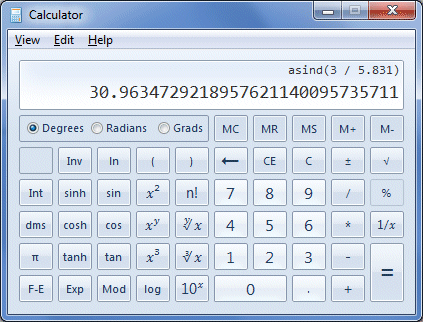
The calculator displays the value of angle θ
You may have been wondering about the sine value for an angle that is greater than ninety degrees (90°). To see an interactive demonstration of how sine values vary as the central angle subtended by a half-chord increases beyond ninety degrees, click here (note: your browser must support Java in order for the interactive page to work). The interesting thing to note here is that as the angle of rotation increases beyond ninety degrees, the half-chord moves into a new quadrant. The central angle subtended by the half-chord therefore actually starts to get smaller again. The series of screen shots below further illustrate the point (we have added the quadrant numbers to the screen shots for clarity). The demo makes use of the Unit Circle. This is a circle that has its centre (shown here as point O) at the origin of a Cartesian coordinate system. The circle has a radius of one unit, so the length of the half-chord at any point is equal to the (absolute) value of the sine of the central angle subtended by the half-chord.
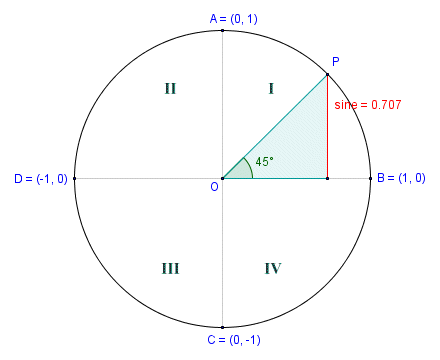
The half chord in Quadrant I
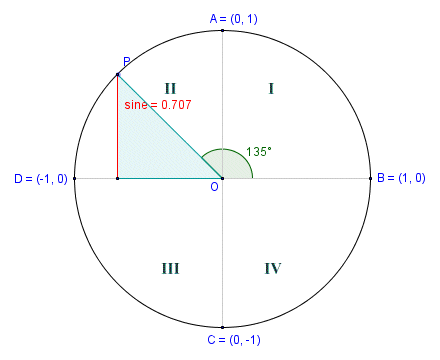
The half chord in Quadrant II
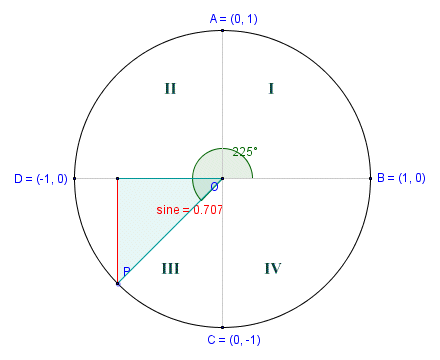
The half chord in Quadrant III
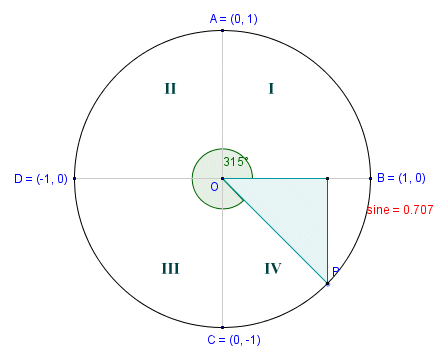
The half chord in Quadrant IV
The angle of rotation in the first quadrant is forty-five degrees (45°), and is therefore the same as the angle subtended by the half-chord. In the second screenshot, we have increased the angle of rotation by ninety degrees to one hundred and thirty-five degrees (135°). The half-chord is now in the second quadrant, but the central angle subtended by the half-chord is once again forty-five degrees. We see the same thing in the third and fourth quadrants. The angle of rotation continues to increase as we move point P anti-clockwise around the circumference of the circle, but the central angle subtended by the half-chord in each quadrant will never exceed ninety degrees.
This raises an interesting question about both the definition of the sine function and its sign in relation to the unit circle. Both the sine and the cosine functions can be defined in terms of a point lying on the circumference of the unit circle. That point is the point at which the half-chord touches the circumference of the unit circle (point P on the diagrams shown above). The angle θ to which the sine corresponds is the angle between the positive x-axis and the radius joining point P and the centre of the circle O, measured anti-clockwise. The sine of this angle is defined to be the y-coordinate of point P. We can express this simply as:
sin (θ ) = y
By definition, therefore, the sine function has values in the range one to minus one (1 to -1). In the first two quadrants (the two quadrants above the x-axis), those values will always be between zero and one, since y will always be equal to or greater than zero. In the third and fourth quadrants, (the two quadrants below the x-axis), the values will always be between zero and minus one, since y will always be equal to or less than zero. The sines of the angles zero degrees (0°), ninety degrees (90°), one hundred and eighty degrees (180°) and two hundred and seventy degrees (270°) will be zero (0), one (1), zero (0) and minus one (-1) respectively.
The sine function is frequently used in various scientific, engineering, and even business applications to model the behaviour of cyclic phenomena. A sine wave (one complete cycle of which is illustrated below) is used to represent a smooth, repetitive oscillation.
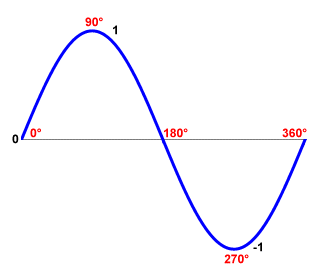
A single cycle of a sine wave
A sine wave is essentially a graph of the way in which the value of y varies over time. The cycle begins at an angle θ of zero degrees (0°), at which point both sin(θ ) and y are zero. Angle θ increases smoothly in the positive direction until it reaches ninety degrees (90°), at which point sin(θ ) is one (1) and y is at its maximum positive value. As the angle increases from ninety degrees to one hundred and eighty degrees (180°), both sin(θ ) and y will move back towards zero. Once the angle exceeds one hundred and eighty degrees, sin(θ ) and y both become negative. At two hundred and seventy degrees (270°), sin(θ ) is minus one (-1) and y is at its maximum negative value. As the angle increases from two hundred and seventy degrees to three hundred and sixty degrees (360°), both sin(θ ) and y will move back towards zero. The simple animation below illustrates how this works.

Sine wave animation
Note that, while an angle of three hundred and sixty degrees marks the end of one complete cycle, its position on the sine wave can also be defined as the starting point for the next full cycle (i.e. zero degrees). Sine waves can describe numerous kinds of cyclic phenomena, such as sound or electromagnetic waves, the movement of a pendulum, or the rotation of a wheel. In its most basic form, a sine wave is a function of time that is described by the formula:
y (t) = A · sin (ωt + φ)
where:
A = the amplitude of the function (the maximum absolute value of y)
ω = the angular frequency (usually measured in in radians per second)
t = the elapsed time
φ = the phase, i.e. the angle (in radians) when t = 0
The mains electricity supply that comes into your home is a good example of a sine wave. The AC (alternating current) electricity supply in the United Kingdom oscillates between peak positive and negative voltages of about three hundred and twenty five volts (325V), so its amplitude is three hundred and twenty five. Each complete cycle (i.e. the time required for the voltage to change from zero, through its peak positive and negative values, and back to zero) takes one fiftieth of a second (0.02 seconds). This gives an angular frequency of 2π radians multiplied by fifty hertz (i.e. 100π radians per second). Factors such as elapsed time and phase are not usually a significant issue for mains electricity, since the supply of electricity is continuous. It does however become critically important when we are dealing with things like high frequency synchronous or asynchronous communications signals.
