An angle is formed when two line segments or rays (the sides of the angle) meet at a common end point (the vertex). Actually, two angles are formed. Usually, one of these angles will be less than one hundred and eighty degrees (i.e. it will be an acute angle, a right angle or an obtuse angle), while the other angle will be greater than one hundred and eighty degrees (i.e. a reflex angle). Sometimes both angles will be straight angles (i.e. they will both be exactly one hundred and eighty degrees). If you need a more detailed perspective on angles generally, it might be helpful to read the page entitled "Angles" in the Geometry section. Trigonometry is primarily concerned with the measurement of angles.
Of course, we can measure angles drawn on paper easily enough using a protractor, although the accuracy of the measurement depends on both the skill of the person measuring the angle and on how accurate the drawing is to start with. There are many situations, however, where we can't use a simple device like a protractor to measure an angle. We must instead derive a value for the angle through calculations based on available information. Trigonometry provides a number of functions that allow us to make calculations involving angles. The trigonometric function (or functions) used for a particular situation will depend on what information we have, and what values we are trying to find.
The size of an angle is determined by how much one of the sides needs to be rotated about the vertex in order to lie directly over the other side. The amount of rotation required is usually measured in either degrees or radians. One degree of arc (to give it its full title) represents a rotation of one three hundred and sixtieth (1/360) of a full circular rotation. The degree can be further sub-divided into sixty equal intervals called arcminutes (or just minutes), and each arcminute can also be sub-divided into sixty equal intervals called arcseconds (or just seconds). There is a tendency nowadays to use decimal notation for the fractional part of a degree, but minutes and seconds are still sometimes used. The following angle values are equivalent (note that the arcminute and arcsecond are denoted by a tick mark and a double tick mark respectively):
45.16°
45° 9' 36"
A radian is the angle subtended at the centre of a circle by an arc of the circle whose length is equal to the radius of the circle. Conversion between angles measured in degrees and angles measured in radians is relatively straightforward. Since the total circumference of a circle is given as 2πr, and since one radian is the angle subtended by an arc of the circle of length r, then the value of one radian in degrees is given as:
Conversely, the value of one degree in radians is given as:
For problems involving trigonometry, the value of an angle may be stated in either degrees or radians. It is therefore useful to know how to convert between the two, should the need arise. Be aware also that most scientific calculators can perform trigonometric calculations in either degrees or radians. You should make sure that your calculator is set to the correct mode when using trigonometric functions, or you may get some unexpected results. The Microsoft Windows calculator (found under Programs>Accessories), when in Scientific mode, can be set to degrees, radians or gradians by selecting the appropriate radio button (the gradian is a rarely-used unit of angle that is equal to one four-hundredth of a turn).
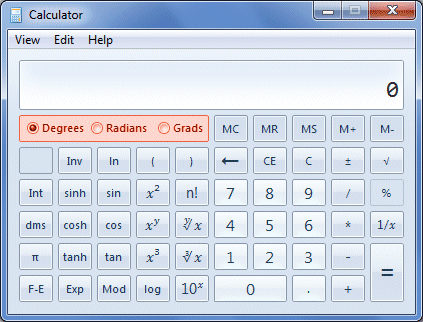
The Microsoft Windows calculator can be set to degrees, radians or gradians
The continued use of the degree as a unit of angle measurement in the modern age may seem a little strange when we take into account the fact that it originated some thousands of years ago. The division of a circle into three hundred and sixty parts is usually accredited to Babylonian astronomers. The number was probably chosen because it is compatible with the sexagesimal number system used by the Babylonians, and because it is almost the same as the number of days in the year. As it happens, three hundred and sixty (360) is actually a very convenient number to work with, because it allows various common fractions of a circle to be represented using a whole number of degrees.
The radian, on the other hand, is often considered to be the natural unit of measurement for angles when working with trigonometric functions. The reason for this is that it is often simply more convenient. The number of radians in a complete rotation is 2π. Trigonometric functions are often used to solve equations that involve the term 2π as a factor. Working in radians often means that we can eliminate the term 2π from our calculations altogether, simplifying the solution of the equation, and reducing the effect of rounding errors. If the outcome must be expressed in degrees, the conversion can be made at the end, after all of the calculations have been completed.
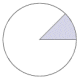
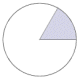
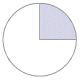
The following table shows the graphic representation of several frequently occurring angles as fractions of a circle, together with their values expressed in both degrees and radians. Familiarity with these angles, whilst not strictly essential to the study of trigonometry, can help students to understand the relationship between degrees and radians. It can also foster a better understanding of the way in which the various trigonometric functions actually work. For the angles shown, we have adopted the convention that the initial side of the angle is the x-axis in the Cartesian plane, and the angles are all positive angles (i.e. the degree of rotation is measured anti-clockwise from the initial side to the terminal side). Note that the radian values are expressed in terms of pi (π). This allows more precision than the equivalent decimal representations.
Common Fractions of a Circle
| Angle |
Fraction |
Degrees |
Radians |
Angle |
Fraction |
Degrees |
Radians |
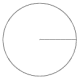 |
0 |
0° |
0 |
 |
|
135° |
|
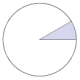 |
|
30° |
|
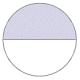 |
|
180° |
π |
 |
|
45° |
|
 |
|
225° |
|
 |
|
60° |
|
 |
|
270° |
|
 |
|
90° |
|
 |
|
315° |
|

|
|
120° |
|

|
1 |
360° |
2π |
Finding the size of an angle is relatively easy, if the angle is formed by two line segments or rays that converge at the centre of a circle of known radius, and the arc subtending the angle (known as the central angle) can be measured. Consider the illustration below. Angle θ is the central angle subtended by arc s at the centre of a circle of radius r. If we have values for r and s, we can find angle θ.
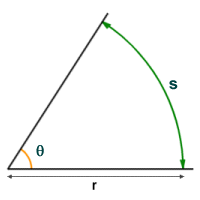
Arc s subtends angle θ
The value of angle θ in radians is given by:
We can also find the value of θ in degrees using:
Conversely, you can probably see from the above that if we know the radius of the circle and the value of angle θ in radians we can find the length of arc s as follows:
s = rθ
If the value of angle θ is given in degrees, the length of arc s would be:
Note that the size of an angle is unrelated to the length of its sides. Imagine a positive angle drawn in the x-y plane that has its vertex at the origin of the coordinate system (0, 0), with the initial side of the angle coincident with the x-axis, as shown in the illustration below. The sides of the triangle may extend away from the vertex indefinitely.
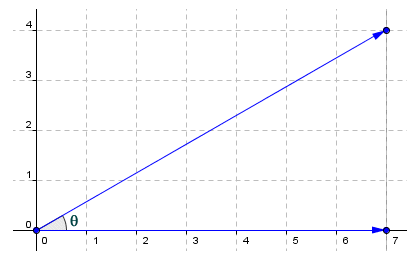
The sides of an angle may extend indefinitely away from the vertex
In order to calculate the value of angle θ, we need some numbers to work with. Of course we could find the x and y coordinates of two points on the terminal side of the angle, and then use algebra to find the slope of the line (see the page entitled "Linear Equations" in the Algebra section). This would give us the tangent of angle θ, and we could use the arctan function on the calculator to find the angle. That, however, would be getting way ahead of ourselves. For now, we will try and find the angle without actually using trigonometric functions. We can start by drawing a circle of known radius, centred at the origin of the coordinate system (which is also the vertex of angle θ). In the illustration below, a circle of radius r = 2 has been added. The arc that subtends angle θ is shown in red.
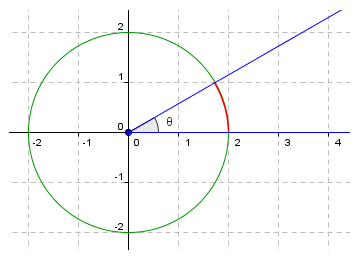
Angle θ is subtended by an arc of a circle of radius r = 2, centred at the origin
We know the radius of the circle (since we chose it!), so all we need to do is measure the length of the arc, and we will then have sufficient information to calculate the angle. Measuring the length of an arc, however, is not particularly easy to do. That's probably why the ancient Greeks chose instead to use to use chords to measure the angles subtended by an arc of a circle. A chord is the line segment that connects two points on the circumference of a circle. If those two points coincide with the ends of an arc, the chord is said to subtend the arc. The chord that subtends an arc will naturally subtend the same central angle, but is easier to measure because it is a straight line. For any given central angle, the ratio of the chord that subtends the angle and the diameter of the circle will be a constant value. The Greeks exploited this fact to derive a method for measuring angles. The page entitled "Chords" in this section explores these concepts further.















