| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The law of sines, sometimes called the sine rule, is an equation that expresses the relationship between the lengths of the sides of a triangle and the sines of its angles, regardless of the type of triangle involved. It is believed to have first been formally stated in the writings of Arab mathematicians dating back to the thirteenth century CE. The law of sines essentially states that for any triangle, the ratio of the length of one side of the triangle to the sine of the angle opposite that side will be the same for all three sides. Consider the triangle below.
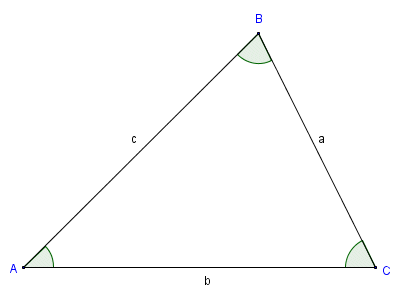
Conventional labelling of the sides and angles of a triangle
We have used the standard notation for labelling the triangle. The vertices are labelled using the upper case characters A, B and C. The side opposite each vertex is labelled with the corresponding lower case character, so that side a is opposite vertex A, side b is opposite vertex B, and side c is opposite vertex C. The upper case characters used to identify each vertex will also be used to identify the angle formed by the sides meeting at that vertex. We can therefore express the law of sines as follows:
| a | = | b | = | c |
| sin (A ) | sin (B ) | sin (C ) |
We can use the law of sines to find the lengths of two sides of a triangle, providing the length of the other side and the size of two angles are known. We can also use the law of sines to find the missing values when we are given the lengths of two of the sides and the size of one of the (non-included) angles, although in this situation there can sometimes be two possible results for the size of the enclosed angle. We will discuss how to deal with this scenario in due course. How do we know that the law of sines does what we say it can do? In other words, how do we actually arrive at the equation shown above? Let's look again at the triangle we saw earlier.
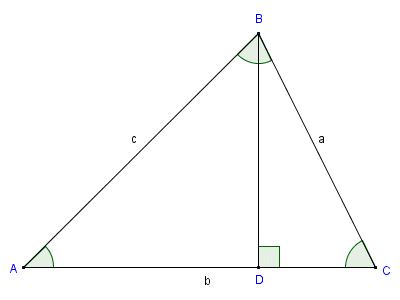
Line segment h is the altitude of triangle ABC
We have drawn the vertical line segment connecting angle B to side b, thereby creating two right-angled triangles. We can now use the definition of the sine of an acute angle θ in a right-angled triangle, which is:
| sin (θ ) = | opposite |
| hypotenuse |
Now consider these two right-angled triangles. Line segment h is common to both triangle ABD and triangle BCD. In fact, for angle A and angle C, in their respective right-angled triangles, line segment h will be the opposite. We can therefore conclude that:
| sin (A ) = | h |
| c |
and
| sin (C ) = | h |
| a |
therefore
h = c · sin (A ) = a · sin (C )
and
| a | = | c |
| sin (A ) | sin (C ) |
Let's repeat the exercise, but this time we will draw the line segment from vertex A to side a so that the line segment is perpendicular to side a.
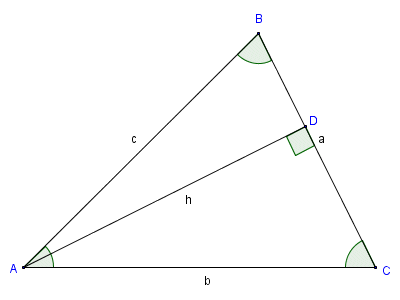
Line segment AD is perpendicular to line a
Once again, we have created two right-angled triangles, triangle ABD and triangle ACD. Again, line segment h is common to both. So, for angle B and angle C, in their respective right-angled triangles, line segment h will be the opposite. We can therefore conclude that:
| sin (B ) = | h |
| c |
and
| sin (C ) = | h |
| b |
therefore:
h = c · sin (B ) = b · sin (C )
and
| b | = | c |
| sin (B ) | sin (C ) |
We have seen how the law of sines works in theory. In order to show how it can be put to practical use, let's look at some examples. Consider the diagram below.
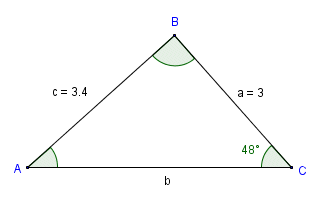
In triangle ABC, we know the length of two sides and the size of one non-included angle
Here, we are given the length of two sides (sides a and c) and one non-included angle (angle C ). We are going to find the length of side b and the sizes of angles A and B. We already know that a = 3, c = 3.4, and C = 48°. We'll start by finding the size of angle A. Using the law of sines, and substituting known values, we get:
| 3 | = | 3.4 |
| sin (A ) | sin (48) |
Rearranging gives us:
| sin (A ) = | 3 · sin (48) |
| 3.4 |
sin (A ) = 0.656
A = sin-1 (0.656) = 40.97°
Since the sum of the internal angles of a triangle must always add up to one hundred and eighty degrees, finding the size of angle B is relatively straightforward:
B = 180° - 48° - 40.97° = 91.03°
We can now apply the law of sines to find the length of side b:
| b | = | 3.4 |
| sin (91.03) | sin (48) |
Rearranging gives us:
| b = | 3.4 · sin (91.03) |
| sin (48) |
b = 4.574
Let's have a look at another example. Consider the diagram below.
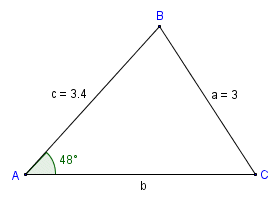
In triangle ABC, we know the length of two sides and the size of one non-included angle
Here, we are given the length of two sides (sides a and c) and one non-included angle (angle A ). We are going to find the length of side b and the sizes of angles A and B. We already know that a = 3, c = 3.4, and A = 48°. Wait a moment though. This scenario looks somewhat familiar! Didn't the previous example have sides a and c of exactly the same lengths? Did it not also have a non-included angle of forty-eight degrees? If you refer back to the previous example you will see that yes, it did indeed have two sides and a non-included angle with the same values. In the previous example, however, it was angle C that was given as forty-eight degrees and not angle A. Does all this mean we are going to get the same results for the missing side length and angles? Let's see.
As before, we are given the length of sides a and c. This time we are given the size of non-included angle A. We are therefore going to find the length of side b and the sizes of angles B and C. We'll start by finding the size of angle C. Using the law of sines, and substituting known values, we get:
| 3.4 | = | 3 |
| sin (C ) | sin (48) |
Rearranging gives us:
| sin (C ) = | 3.4 · sin (48) |
| 3 |
sin (C ) = 0.842
C = sin-1 (0.842) = 57.35°
Remember that the sum of the internal angles of a triangle must add up to one hundred and eighty degrees, so we can easily find the size of angle B:
B = 180° - 48° - 57.35° = 74.65°
We can now apply the law of sines to find the length of side b:
| b | = | 3 |
| sin (74.65) | sin (48) |
Rearranging gives us:
| b = | 3 · sin (74.65) |
| sin (48) |
b = 3.893
This is obviously a different set of results from the one we obtained previously. This serves to highlight the fact that, for any two triangles, simply having two sides of the same length and one (non-included) angle in common does not guarantee that the triangles are congruent. If you want to refresh your memory about the conditions that must be true in order to establish the congruency of two triangles, have a look at the page entitled "The Triangle" in the Geometry section. In an exam question, you will usually be told which of the two sides for which the lengths are known is opposite the given (non-included) angle. However, there is another possibility with this type of problem of which you should be aware.
Even if you know which of the two given sides is opposite the given (non-included) angle, there could still be more than one possible outcome for a problem of this type. Suppose you are given an exam question in which you are given the size of angle A and the lengths of sides a and c, but are not provided with a diagram. Surely there is no problem here, since we know that side a is opposite angle A, and that side c is opposite angle C. Can't we just substitute values for angle A and sides a and c into the law of sines equation to find angle C? You could certainly be forgiven for thinking so, but consider the diagram below.
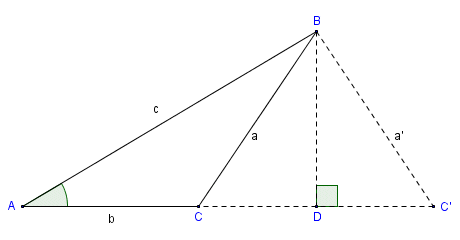
In the ambiguous case, we can construct two triangles using the information given
You might have already spotted the problem. We can actually construct two different triangles, triangle ABC and triangle ABC', that have the given parameters. Angle A is common to both triangles, as is side c. In triangle ABC, side a is opposite angle A. Likewise, in triangle ABC', side a' is opposite angle A, and is the same length as side a. A situation such as this, in which there are two possible values for each of the unknown components, is known as the ambiguous case. In order for this situation to occur, the following conditions must apply:
In the above diagram, all of the conditions required by the ambiguous case are met. This means that we have two possible solutions to the problem. Note that the altitude of both triangle ABC and triangle ABC' is represented by line segment BD. Triangles BCD and BC'D are therefore congruent (they have one leg in common, and the hypotenuse of triangle BCD (side a) is equal in length to the hypotenuse of triangle BC'D (side a'). This means that angle C' is equal to angle BCD, which is the supplementary angle to angle C. In other words:
C ' = ∠BCD = 180° - C
In the ambiguous case, the angle we are looking for may be either acute or obtuse, and the two possible values will be supplementary angles (i.e. they will sum to one hundred and eighty degrees). The sine of the angle will be the same in either case. You can check this out for yourself using your calculator, or by examining a table of sine values. Just find the sine values for any pair of angles that sum to one hundred and eighty degrees. They will be the same.
We said earlier that we could also use the law of sines to solve a triangle if we knew the length of one of the sides and the size of two of the angles. Obviously, finding the size of the third angle is a trivial exercise, since the internal angles of a triangle must always sum to one hundred and eighty degrees. We need to apply the law of sines, however, to find the lengths of the other two sides. Consider the diagram below.
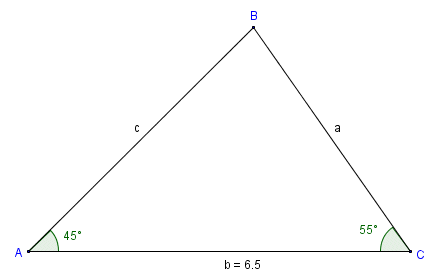
In triangle ABC, we know the size of two angles and the length of one side
Since the side we are given the length of is opposite the only angle we were not given the size of, the first thing we need to do is to find the size of the missing angle. This is easy enough to do, since we simply need to subtract the sum of the other two angles from one hundred and eighty degrees:
B = 180° - (45° + 55°) = 80°
We can now use the law of sines equation to find the length of side a:
| a | = | 6.5 |
| sin (45) | sin (80) |
Rearranging gives us:
| a = | 6.5 · sin (45) | = 4.667 |
| sin (80) |
Similarly, we can use the law of sines equation to find the length of side c:
| c | = | 6.5 |
| sin (55) | sin (80) |
Rearranging gives us:
| c = | 6.5 · sin (55) | = 5.407 |
| sin (80) |
We can also use the law of sines to find the radius of a triangle's circumscribed circle. The circumscribed circle of a triangle is the unique circle whose circumference passes through all three of the triangle's vertices. It turns out that the ratio of the side of a triangle to the sine of the angle opposite that side is equal to the diameter of the triangle's circumscribed circle. We can express that algebraically in terms of the circle's radius, using a slightly amended version of the law of sines equation:
| a | = | b | = | c | = 2r |
| sin (A ) | sin (B ) | sin (C ) |
Click here to see an interactive demonstration of the unit circle as the circumscribed circle of a triangle. The demo uses the unit circle to show how the sine of each angle and the length of the side opposite each angle will vary as the vertices of the triangle are moved around the circumference of the unit circle. You will see that for each angle, the ratio of the length of the side and the sine of the angle remains constant as the shape of the triangle changes. You will also see that for the unit circle, the ratio is equal to the diameter of the circle (i.e. two units, or twice the radius of the unit circle). This relationship will hold true for the circumscribed circle of any triangle (note: your browser must support Java in order for the interactive page to work).