| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
A circle is a simple shape consisting of the points that lie in a two-dimensional plane equidistant from some common point (the centre of the circle) in that plane. Circles are often named after the point defined as the centre of the circle, so in the example shown below we might refer to the circle as circle A. The shape is in fact an example of a simple closed curve (sometimes called a Jordan curve, after French mathematician Camille Jordan). According to the Jordan curve theorem, a simple closed curve partitions the plane in which it lies into two regions - an interior region bounded by the curve, and an exterior region containing all of the exterior points, so that a continuous path connecting any point in one region to any point in the other region must intersect the curve at some point. Although this might appear intuitively obvious, providing a mathematical proof is a far from easy task.
A circle is an example of a simple closed curve
Mankind has been aware of the circle as a geometric shape since the dawn of history, and there are countless examples of circles that occur in the natural world. Both the sun and the full moon appear as circular shapes in the sky. The eyes of many animals, birds, fish and insects are circular in shape, as are various fruits and berries. You can probably think of many more examples that occur in nature. The circle is also a very important shape in many fields of human endeavour, including science and engineering. One of the earliest and most important inventions in the history of civilisation, for example, was the wheel. The pipes that carry our water and gas, and the cables that carry electrical power and communication signals, all have a circular cross section. Even the coinage we use and the plates that we eat from are more often than not circular.
The total length of a closed curve is called its circumference. In fact, although the word circumference can be applied to the length of any closed curve, it is most often associated in people's minds with the circle. It can also be used to refer to the perimeter formed by the closed curve, i.e. the boundary separating the interior region of the circle from the exterior region. In fact, the circle encloses the greatest possible area of any closed curve having a given circumference. As well as creating two distinct regions, a circle can be seen as separating all points in a plane into three distinct groups: those inside the circle, those outside the circle, and those that lie on the perimeter of the circle.
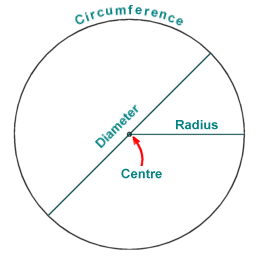
A circle has a centre, a radius, a diameter and a circumference
The distance between the centre of the circle (sometimes called the origin) and any point on the circumference is called the radius. The length of a line segment between any two points on the circumference that bisects the centre of the circle is called the diameter. The diameter is always exactly double the length of the radius, and is the largest distance that can exist between any two points that lie on the circumference. As well as referring purely to a distance, the term radius may also be used to refer to a specific line segment that connects the centre of the circle to some point on the circumference. Similarly, the term diameter may be used to a specific line segment that joins two points on the circumference and intersects the centre of the circle.
Pi (usually written as the Greek letter π in mathematical expressions) is an important mathematical constant that represents the ratio of the circumference of a circle to its diameter. The value of Pi is very approximately equal to three point one four (3.14). Pi is an irrational number, which means that it cannot be expressed exactly as a fraction that has integer values in both the denominator and the numerator. As a result, the decimal representation of Pi is non-terminating (the pattern of numbers following the decimal point is non-repeating, and the number of places after the decimal point is indeterminate). In fact, the quest for an ever more accurate value of Pi continues (a value for Pi involving some ten trillion digits has apparently been calculated as recently as 2011). For our purposes, a much less accurate approximation is perfectly acceptable. In fact, even cosmologists are happy with a value for Pi involving only thirty-nine digits, which would allow them to calculate the diameter of the universe to a precision of one atom!
For a circle of circumference C and diameter d, Pi can be expressed as follows:
| π = | C |
| d |
For convenience, because we are more often given the radius r of a circle than the diameter, the formula for the circumference of a circle is usually written as:
C = 2πr
It can also be shown that the area of a circle is proportional to the square of its radius. In the third century BCE, the Greek mathematician Archimedes proved that the area enclosed by a circle is equal to the area of a triangle with a base length equal to the circle's circumference, and a height equal to the circle's radius. We have already established that the circumference of a circle is equal to Pi multiplied by the diameter of the circle. Since the area of a triangle is equal to half the product of its base length and height, the area of the circle must therefore be equal to Pi multiplied by the radius of the circle squared. The ratio of the area of a circle to the area of the square of its radius is thus identical to the ratio of the circumference of a circle to its diameter, in other words Pi. As shown in the illustration below, the area of the circle is thus equal to the area of the shaded area (r 2) multiplied by Pi.
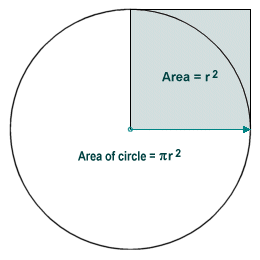
The area of a circle is equal to the square of its radius multiplied by Pi
To express this as a formula, the area of a circle is given by:
Area = πr 2
An arc of a circle is some part of its circumference. A sector is a region within the circle that is enclosed by two radii, and an arc that connects the points at which the radii meet the circumference (somewhat similar in shape to a slice of pizza). The angle formed by the intersection of the two radii forming a sector is called the central angle. This angle is, by definition, the angle subtended by the arc that completes the sector. The diagram below illustrates the relationship between arcs and sectors (the Greek letter θ is used to represent the central angle).
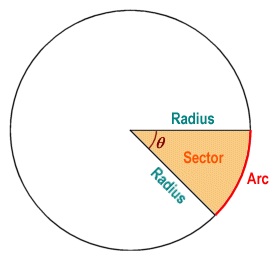
A sector is bounded by two radii and an arc
For any arc, if you know the value of the angle θ subtended by the arc and the length of the radius r, you can find the length of the arc using the following formula:
| Arc length = | 2πr θ |
| 360 |
Or alternatively, you can use this equivalent formula:
| Arc length = | πr θ |
| 180 |
Note that if the angle is given in radians, the formula becomes simply:
Arc length = r θ
Also for any arc, where you know the value of the angle θ subtended by the arc and the length of the radius r, you can find the area of the sector using the following formula:
| Area of sector = | θπr 2 |
| 360 |
Note that if the angle is given in radians, the formula becomes simply:
| Area of sector = | θr 2 |
| 2 |
Sectors are considered to be congruent (i.e. they have the same shape and size) if they contain the same central angle, and are formed by radii of the same length. Two sectors that contain the same central angle will thus be congruent if they belong to the same circle (in which case the radii forming the central angle for both sectors will be of the same length), or if they belong to different circles that are themselves congruent (in which case the radii forming the central angle for both sectors will still be of the same length). Looking at this from another perspective, if two sectors have the same arc length and belong either to the same circle or to two congruent circles, both arcs will subtend the same angle and the sectors will be congruent. In the illustration below, circles A and B are congruent, and the central angle for each of the sectors a, b and c is θ, therefore sectors a, b and c are congruent.
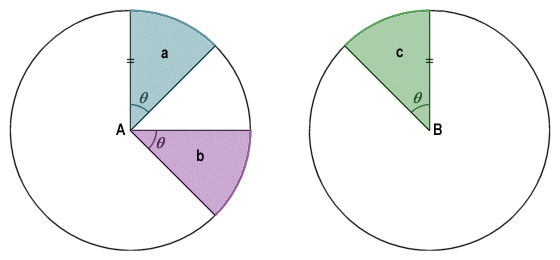
Circles A and B are congruent, as are sectors a, b and c
A chord is any line segment within a circle for which the end points both lie on the circumference of the circle. By definition, a diameter is also a chord since its end points lie on the circumference of the circle. A diameter of a circle is in fact the longest chord that can exist for that circle, since it passes through the centre of the circle. All diameters of a circle are chords, and all chords that pass through the centre of the circle are diameters (indeed, any chord that does not pass through the centre of the circle cannot be a diameter). In the diagram below, all of the line segments shown are chords.
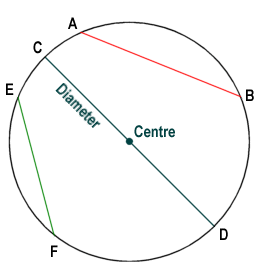
Line segments AB, CD and EF are all chords. Line segment CD is also a diameter
If a radius of a circle bisects a chord, then the radius is also perpendicular to that chord. Conversely, if a radius is perpendicular to a chord, then the radius bisects that chord. In fact, any line that is perpendicular to a chord passes through the centre of the circle to which that chord belongs. In the diagram below chord AC is perpendicular to radius r, which intersects it at point B. Radius r therefore bisects chord AC, and line segments AB and BC are equal in length.
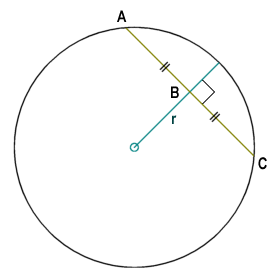
Radius r is the perpendicular bisector of chord AC
If two chords in the same circle (or two chords in congruent circles) are the same perpendicular distance from the centre of the circle, then the chords are congruent (i.e. they are of the same length). Conversely, if two chords in the same circle (or two chords in congruent circles) are congruent, then they are at the same perpendicular distance from the centre of the circle. In the diagram below, circles C1 and C2 are congruent. Chords AB, CD and EF are all at the same perpendicular distance from the centre of their respective circles. Therefore, chords AB, CD and EF are congruent.
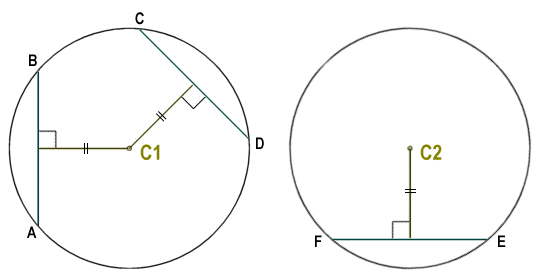
Chords AB, CD and EF are congruent
Consider the diagram below, which shows a circle with two intersecting chords.
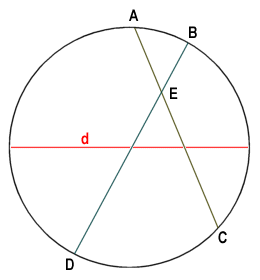
Chords AC and BD intersect at point E
For two chords AC and BD that intersect at point E, it can be shown that the product of the lengths of line segments AE and CE is equal to the product of the lengths of line segments BE and DE. Furthermore, it can be shown that the sum of the squares of the lengths of line segments AE, CE, BE and DE is equal to the square of the length of the diameter d. These relationships can be expressed algebraically as follows:
AE · CE = BE · DE
AE2 + CE2 + BE2 + DE2 = d2
The line perpendicular to a chord that connects the mid-point of the chord to a point on the circumference of the circle is called a sagitta (or versine). If the length x of the chord and the length y of the sagitta are known, we can calculate the radius r of the circle using the following formula (derived from the Pythagorean theorem):
| r = | x2 + y2 |
| 2y |
Where r is the radius of the circle, y is the length of the sagitta, and x is half of the chord length.
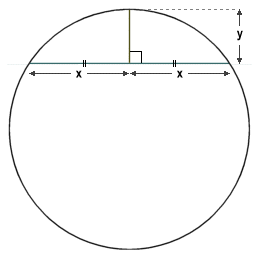
If the values of x and y are known, the radius can be calculated
If the angle subtended by the chord at the centre of the circle is ninety degrees (90°) and the radius r of the circle is known, then the length l of the chord can be calculated using the following formula (note that if the central angle is not ninety degrees, trigonometry will be required to calculate the chord length):
l = r √2
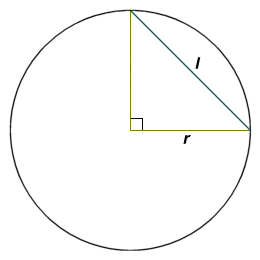
Chord length can be calculated if the chord subtends a central angle of 90°
Finally, consider the diagram below. It can be shown that the length of the perpendicular line segment BD that connects a point on chord AC to a point on the circumference of the circle to which it belongs, multiplied by the diameter d of the circle, is equal to the product of the lengths of line segments AB and BC (i.e. the distances between point B and the ends of the chord). This relationship can be expressed using the following equation:
BD · d = AB · BC
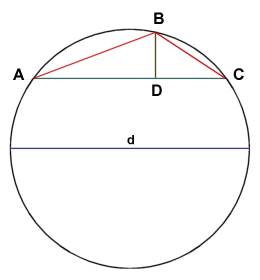
The product of BD and d is equal to the product of AB and BC
A segment is a region of a circle bounded by a chord and the arc subtended by the chord (i.e. the arc that lies between the end points of that chord). Assuming that the radius r of the circle, the length l of the chord, the perpendicular distance h from the chord to the centre of the circle, and the central angle θ are known, the area of a segment can be found. First calculate the area of the sector associated with the segment (see above). Next, calculate the area of the triangular portion of the sector, and subtract the result from the total area of the sector to leave the area of the segment. Note that if neither the length of the chord nor its perpendicular distance from the centre is known, the area of the segment can still be calculated, but the calculation will involve trigonometry. In the illustration below, the segment is the area shaded in pale blue.
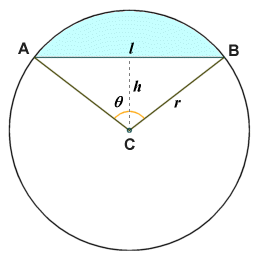
A segment is a region of a circle that is bounded by a chord and the arc it subtends
| Area of sector (a1) = | θπr 2 |
| 360 |
| Area of triangle ABC (a2) = | lh |
| 2 |
Area of segment = a1 - a2
Note that if only l and r are known, h can be found using Pythagoras' theorem:
h = √((0.5l)2 + r 2)
Similarly, if only h and r are known, l can be found using Pythagoras' theorem:
l = 2√(r 2 - h2)
A tangent (in the context of circles) is a line or line segment that touches a circle only at a single point, and is perpendicular to the radius that connects that point with the centre of the circle. From this definition it is also possible to infer that any line perpendicular to a tangent that passes through the point at which the tangent touches the circle must also pass through the centre of the circle. Furthermore, from any point P that is external to the circle, it is possible to draw exactly two tangents from that point to points on the circle (let's call them A and B). The lengths of line segments AP and BP will be equal, as illustrated by the diagram below. If we call the centre of the circle O, then the angles AOB and APB are supplementary (i.e. they add up to one hundred and eighty degrees).
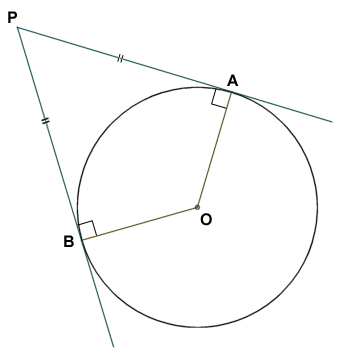
Line segments AP and BP are both tangential to the circle and equal in length
The diagram below illustrates a situation in which line segment PQ is a tangent to a circle at point Q, and line segment QR is a chord of that circle. It can be shown that the magnitude of angle PQR is exactly half that of the central angle subtended by chord QR (i.e. angle QOR). Since line segment OS is the perpendicular bisector of chord QR, the angles QOS and ROS are equal. Angles QOS and OQS sum to ninety degrees (because they are the complementary angles in right-angled triangle OQS), as do angles PQS and OQS. Hence, angles PQS and QOS must be equal, and since angles QOS and ROS are also equal, angle QOR must be twice the magnitude of angle PQR.
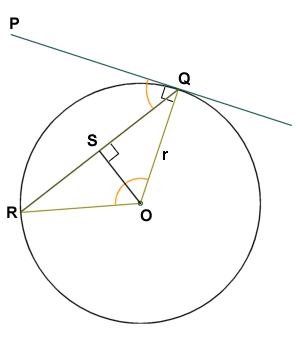
Angle PQR is half the magnitude of angle QOR
If point O has coordinates x0, y0 and point Q has coordinates x1, y1, the equation of the tangent line is:
(x1 - x0) x + (y1 - y0) y = (x1 - x0) x1 + (y1 - y0) y1
or alternatively:
(x1 - x0)(x - x0) + (y1 - y0)(y - y0) = r 2
The slope of the tangent line is also often of interest. Assuming that y1 is not equal to y0, it can be shown that the slope of the tangent is given by the following equation:
| Δy | = | x1 - x0 |
| Δx | y1 - y0 |
The triangular symbol (Δ) in the equation represents the Greek upper case letter Delta, and is used to indicate the difference between two values of a variable (sometimes this symbol is replaced by the lower-case letter d). Note that if y1 is equal to y0, the radius that is perpendicular to the tangent is a horizontal line segment, and the tangent will therefore be a vertical line, with a slope that is undefined. Conversely, if x1 is equal to x0, the radius that is perpendicular to the tangent is a vertical line segment and the tangent will be a horizontal line, with a slope of zero. Note also that if the centre of the circle is the origin (i.e. x0 = 0, y0 = 0), then the slope of the tangent line becomes simply:
| Δy | = | x1 |
| Δx | y1 |
A secant is a line that cuts the circumference of a circle at two points. You can think of it as a chord that extends beyond the circumference of a circle in both directions. In the diagram below, two secants intersect at a point A that is external to a circle. The secants that intersect at point A cut the circle at points B, C, D and E, as shown. The magnitude of the angle formed by the intersection of the secants (angle BAC) is half that of the difference between the angles subtended by the intercepted arcs (arc BC and arc DE), which are angles BOC and DOE respectively.
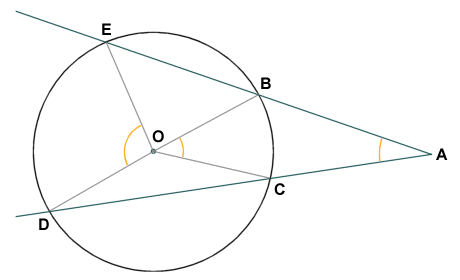
The magnitude of angle BAC is half the difference between angles BOC and DOE
It can also be shown that the product of the lengths of line segments AE and AB is equal to the product of line segments AD and AC:
AE · AB = AD · AC
In the diagram below, a line segment from a point A that is external to a circle is tangential to the circle at point B. A second line segment from point A forms a secant that cuts the circle at points C and D.
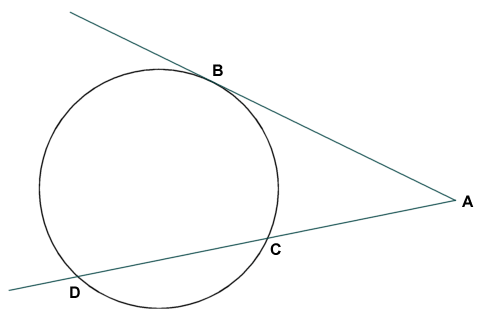
The product of AC and AD is equal to AB2
It can be shown that the length of line segment AB squared is equal to the product of the lengths of line segments AC and AD:
AC · AD = AB2
Two secants may also intersect inside a circle. In the diagram below, two secants intersect at a point E that is inside a circle. The secants that intersect at point E cut the circle at points A, B, C and D, as shown. The magnitude of both of the angles formed by the intersection of the secants (angles AEB and CED) is half that of the sum of the angles subtended by the intercepted arcs (arc AB and arc CD), which are angles AOB and COD respectively.
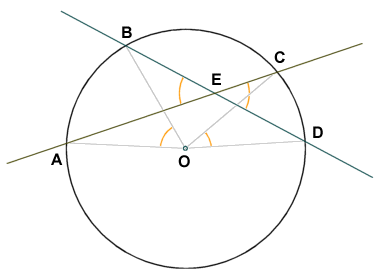
The magnitude of angles AEB and CED is half the sum of angles AOB and COD
An inscribed angle is an angle formed when two chords intersect at a common point on the circumference of the circle to which they both belong. In the example below, the inscribed angle ACB is formed by the intersection of chords AC and BC. The central angle subtended by the arc connecting points A and B (angle AOB) is exactly double the magnitude of angle ACB. This relationship will be the same for any inscribed angle, even if the inscribed angle is obtuse (i.e. greater than ninety degrees). The arc connecting the non-intersecting ends of two chords that form an inscribed angle is called the intercepted arc.
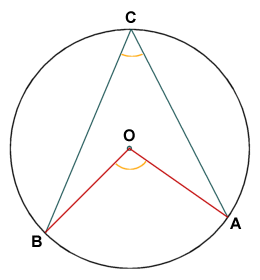
The magnitude of central angle AOB is double that of inscribed angle ACB
If inscribed angle ACB is greater than ninety degrees, central angle AOB will be a reflex angle, i.e. it will have a magnitude that is greater than one hundred and eighty degrees (note that if inscribed angle ACB is exactly ninety degrees, intercepted arc AB will be a semi-circle and central angle AOB will be one hundred and eighty degrees).
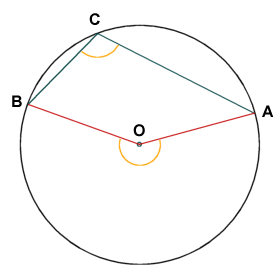
If an inscribed angle is obtuse, the corresponding central angle is a reflex angle
Given that the central angle subtended by an arc will always have exactly double the magnitude of any inscribed angle that intercepts the arc, all inscribed angles that intercept the same arc, and that are on the same side of the chord that connects the end points of the arc, will have the same magnitude as shown below.
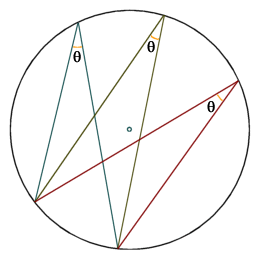
Inscribed angles that intercept the same arc will have the same magnitude
If two inscribed angles intercept the same arc, but are on opposite sides of the chord that connects the end points of the arc, then the inscribed angles will be supplemental (i.e. they will sum to one hundred and eighty degrees).
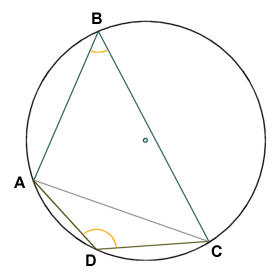
Inscribed angles ABC and ADC are supplementary
If we know the coordinates a and b of the centre of a circle, and the radius r of the circle, then for any point x, y on the circumference of the circle the following equation (called the equation of the circle) will be true:
(x - a)2 + (y - b)2 = r 2
The validity of this equation can be demonstrated graphically, as shown by the illustration below. The radius r of the circle is the hypotenuse of a right-angled triangle in which the length of the horizontal leg is given by x - a, and the length of the vertical leg is given by y - b. The equation is thus simply the application of Pythagoras' theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
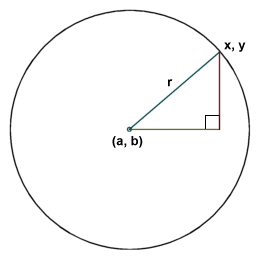
Radius r is the hypotenuse of a right-angled triangle
Note that if the centre of the circle has the coordinates a = 0, b = 0, then the equation simplifies to:
x2 + y2 = r 2
It can be shown that, for any three points on a plane that do not lie on the same line, there exists a unique circle. It is possible to use the equation of the circle to find both the radius of the circle and the coordinates of the centre of the circle, providing the coordinates of all three points are known. Simply substitute the known values of x and y for each point into the equation. This will give you three equations, each of which will have three variables (a, b and r) for which the values are unknown. The unknown values can be found by solving the equations simultaneously.