| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
A pyramid is a polyhedron (i.e. a three-dimensional geometrical shape with flat faces and straight edges). What distinguishes the pyramid from other types of polyhedra is that although one of its faces (the base of the pyramid) is a polygon, and may have three or more sides, all of the other faces are triangles. As you can see from the illustration below, each side of the base forms one side of a triangle that connects the base of the pyramid to its apex. These triangular faces have one vertex in common (the apex of the pyramid) and their number will equal the number of sides forming the base. A pyramid with a base having n sides will have n+1 faces (i.e. one base polygon and n triangular sides). It will also have 2n edges, and n+1 vertices. Note that there is a special type of pyramid called a tetrahedron, for which the base is also a triangle. Tetrahedra have certain special properties, which we will talk about elsewhere. On this page, we will discuss the properties of pyramids in general.

A pyramid has a polygonal base and triangular sides
Various civilisations around the world have, over the last three thousand years or so, built pyramid-shaped structures. Probably the best known, and certainly one of the largest, is the Great Pyramid at Giza, on the outskirts of Cairo in Egypt. The Great Pyramid, also known as the Pyramid of Khufu or Pyramid of Cheops, is the largest and probably the oldest of several pyramids at the Giza site. It is believed to have been built some four and a half thousand years ago as a tomb for the pharaoh Khufu. For several thousand years, it was the largest man-made structure in the world, and is the only one of the original wonders of the ancient world still in existence. The Great Pyramid, like many other Egyptian pyramids, has a square base and is similar in shape to the illustration above. It is believed that the shape of the pyramid (with most of the weight close to the ground) was chosen in order to allow these ancient civilisations to create very large structures that were stable.

The pyramids at Giza, near Cairo, Egypt
There are several factors that determine the type of pyramid. Perhaps the word "type" should be replaced by the word "shape", since there are a potentially infinite number of different shapes for pyramids, many of which do not fall into a particular category. The overall dimensions of the pyramid will of course be a factor. Other than that, the most important differences will be in the shape of the polygonal base (i.e. the number of sides it has, and whether or not it is a regular polygon), and the orientation of the apex of the pyramid with respect to the base (i.e. is the apex positioned over the geometric centre of the base, or is it offset by some distance in a particular direction). The best known form of pyramid is probably the one illustrated above, which has a square base and an apex that is positioned directly over the geometric centre of the base. Here are some other formats commonly encountered:
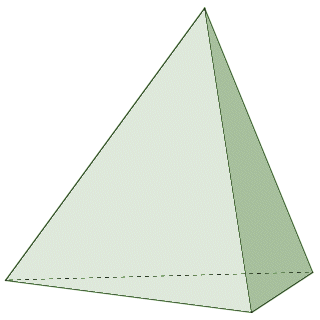
A triangular pyramid (tetrahedron) has a triangular base
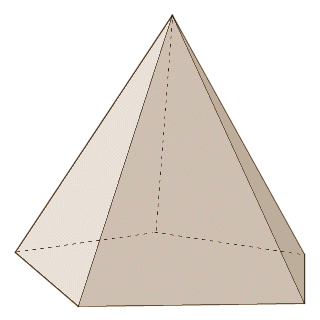
A pentagonal pyramid has a pentagonal base
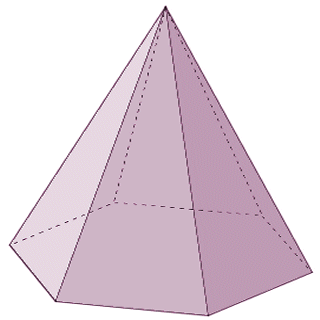
A hexagonal pyramid has a hexagonal base
Only pyramids that have a base polygon with three, four, or five sides may be composed entirely of regular polygons. This requires that every face of the pyramid has sides of equal length, and internal angles of equal magnitude. The base of the pyramid must be an equilateral triangle, a square, or a regular pentagon. The remaining faces must be congruent equilateral triangles with a side length equal to the length of one side of the base polygon. The pyramid itself may be considered to be a regular pyramid if the base if the pyramid is a regular polygon, and the sides of the pyramid are congruent triangles (either equilateral or isosceles). If the base of the pyramid is not a regular polygon (i.e. the lengths of the sides and the magnitudes of the internal angle vary) then the pyramid itself will also be irregular.
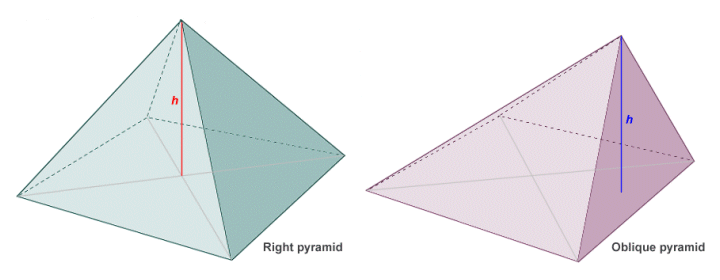
The position of the apex relative to the base is a significant factor
The other feature of interest, as mentioned above, is the orientation of the apex of the pyramid with respect to the base. If the apex is directly over the geometric centre (or centroid) of the base, then the pyramid is said to be a right pyramid. Note that, in order for this to be true, a line segment connecting the geometric centre of the base to the apex would be perpendicular to the plane in which the base lies. If the apex does not lie directly above the geometric centre of the base, the pyramid is said to be an oblique pyramid. An oblique pyramid is by definition irregular (regardless of whether the base polygon is regular or not) because the sides of the pyramid cannot be congruent.
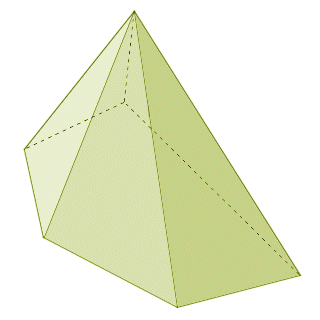
A pyramid with an irregular polygon for a base is itself irregular
The volume V of a pyramid, regardless of the shape of its base or the orientation of its apex, is calculated as one third of its base area times its height (the same is true, incidentally, of a cone). We can formalise this relationship as:
V = 1/3 Bh
where B is the area of the base, and h is the height of the pyramid (i.e. the perpendicular distance from the base of the pyramid to its apex). Finding the surface area of a pyramid can be a little more complicated if the pyramid is irregular, as the base will (usually) be an irregular polygon and the triangular faces will differ in shape. In such a case, the area of each face of the pyramid (including the base) must be found separately, and the values added together to get the total surface area. If the pyramid is a regular pyramid, life is somewhat simpler. The total surface area A is then given as:
A = B + 1/2 pl
where B is the area of the base, p is the length of the perimeter of the base, and l is the slant height of the pyramid (see illustration below). Note that the slant height l of a regular pyramid can be calculated using the following formula:
l = √ (h 2 + r 2)
where h is the height of the pyramid, and r is the the length of the inradius of the base of the pyramid (i.e. the length of the radius of the base's inscribed circle, which is also the distance between the geometric centre of the base and the centre of one of its sides). Finding the area of the base should be relatively straightforward, as the base is a regular polygon. If you need to refresh your memory on the subject, see the page entitled "Regular polygons" in this section. The surface area of a pyramid is often referred to as having two distinct components. The first is the base area (i.e. the area of the base polygon). The second is the lateral area (i.e. the combined surface area of the triangular faces).
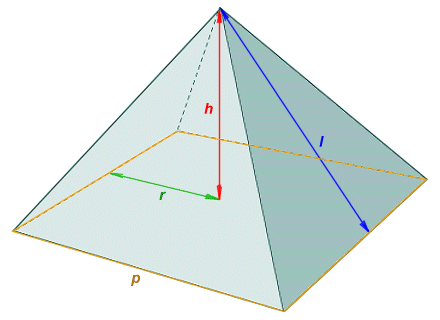
The base perimeter p, height h, slant height l and inradius r of a regular pyramid