| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
A triangle is a polygon (i.e. a two-dimensional, enclosed shape with straight sides) that has three sides and three internal angles (which is why it is called a triangle). A triangle can be created by drawing line segments to connect any three points on a two dimensional plane, providing they do not all fall on the same line (i.e. they are not collinear). Although triangles can vary in both size and appearance, something they have in common (apart from all having three sides and three angles, of course) is that the interior angles of a triangle always add up to one hundred and eighty degrees (180°). There are four main types of triangle you should be familiar with:
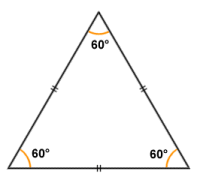
In an equilateral triangle, all sides and all angles are equal
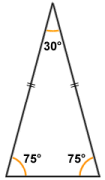
In an isosceles triangle, two sides and two angles are equal
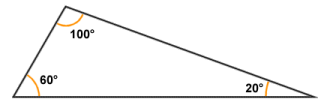
In a scalene triangle, no two sides and no two angles are equal
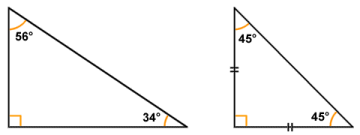
Right-angled triangles may be scalene (left) or isosceles (right)
For any triangle, the sum of the lengths of any two sides will always exceed the length of the third side. This principle is sometimes referred to as the triangle inequality. At the same time, the length of any one side of a triangle will always be greater than the difference between the lengths of the other two sides. The longest side of a triangle will always be opposite the greatest angle, and vice versa. In the event of all the angles being equal, all of the sides will also be equal. In the event of just two of the angles being equal, then the sides opposite those angles will also be equal. If the size of these angles exceeds sixty degrees, then the length of the side opposite the third angle will always be less than that of the other two sides.
The internal (or interior) angles of a triangle are the angles formed at each vertex of the triangle (i.e. where the sides meet) on the inside of the triangular shape. All triangles have three internal angles, one per vertex. If every internal angle of a simple polygon is less than one hundred and eighty degrees ( < 180° ), it is said to be convex. Since by definition a triangle (which is a type of polygon) cannot contain an internal angle of one hundred and eighty degrees or greater, all triangles must be convex polygons.
A triangle is a convex polygon with three internal angles
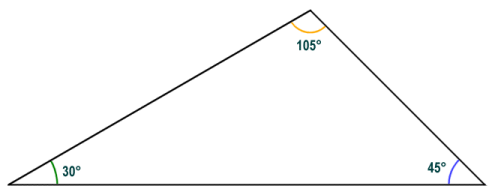
The external (or exterior) angles of a triangle also occur at each vertex of the triangle, but are formed between one side of the triangle and a ray that is extended from the adjacent side. The sum of the internal and external angles at any one vertex of a triangle is always one hundred and eighty degrees (180°). In other words, the external angle of a vertex is supplementary to its internal angle. Since the internal angles of a triangle also always sum to one hundred and eighty degrees, the external angle at any vertex is equal to the sum of the internal angles at the other two vertices. The sum of the external angles of a triangle (or any simple polygon for that matter) is always three hundred and sixty degrees (360°).
The external angle at a vertex is equal to the sum of the internal angles at the other two vertices
The vertices of a triangle are usually labelled using the upper case characters A, B and C. The vertices of the triangle are labelled in order, either clockwise or anti-clockwise. The sides of the triangle are normally labelled using lower-case characters. A commonly used convention is to label the side with the lower-case version of the character used to label the vertex to which it is opposite. In formulae describing various properties of triangles, the label associated with a vertex is often used to represent the internal angle at that vertex. In a similar fashion, the label associated with a particular side is used to represent the length of that side. The following diagram illustrates possible ways in which a triangle might be labelled:
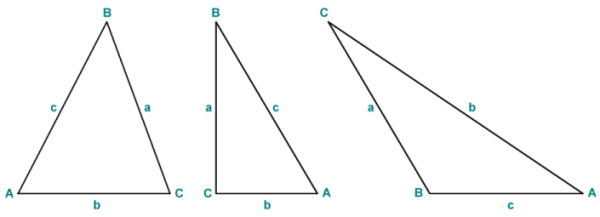
Vertices and side are often labelled using upper and lower-case characters
The area of a triangle is found by multiplying the height of the triangle by the length of its base. The triangle must of course be oriented in such a way that one of its sides is horizontal, and at the bottom of the triangle. The formula works for all triangles, regardless of type, and can be written as:
| area = | base × height |
| 2 |
In order to satisfy yourself that this must be true, consider the following triangle:
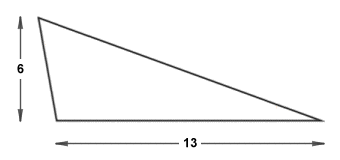
An obtuse scalene triangle
If we create a copy of this triangle and rotate it one hundred and eighty degrees, we can create a parallelogram with the same base and height measurements as our original triangle, but which will have an area twice as large:
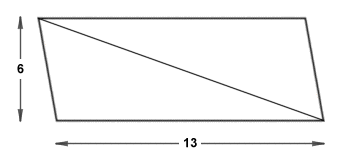
A parallelogram formed from two identical scalene triangles
If we now draw a vertical line segment from the left-hand side of the base of the parallelogram to the top of the parallelogram, we create a right-angled triangle:
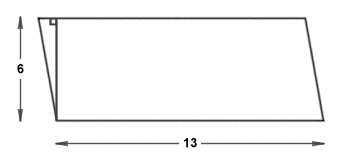
A right-angled triangle is constructed at one end of the parallelogram
We can remove the right-angled triangle from the left-hand end of the parallelogram and attach it to the right-hand end of the parallelogram to create a rectangle with base and height dimensions that are the same as those of both our scalene triangle and the parallelogram we created from it:
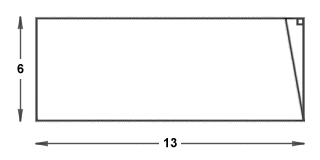
The right-angled triangle is repositioned to create a rectangle
The area of the rectangle is calculated as its base times its height. The area of the rectangle is the same as that of the parallelogram from which it was derived, while the parallelogram itself was formed from two identical triangles. The area of the original triangle must therefore be exactly half that of the rectangle we ended up with. You can follow the procedure described above for any triangle to obtain a rectangle with the same base and height dimensions, and the rectangle will always have an area double that of the original triangle. Note that in the case of a right-angled triangle (providing the side chosen as the base is not the side opposite the right-angle itself), the resulting parallelogram will in fact be a rectangle.
Heron (or Hero) of Alexandria was a Greek philosopher and mathematician who lived in the first century CE. Although he is credited with the invention of a number of mechanical devices, he is perhaps best remembered for his formula for finding the area of a triangle from its side lengths alone. The formula is (unsurprisingly) known as Heron's formula, and is useful for finding the area of an oblique triangle if you don't know the height of the triangle. Consider the triangle below.
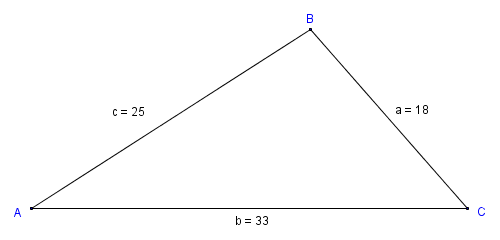
We can use Heron's formula to find the area if the lengths of all sides are known
Heron's formula can be used to find the area of a triangle if the length of all three sides of the triangle are known, and can be stated with reference to triangle ABC (above) as:
area · √(s(s - a)(s - b)(s - c))
where s is the semiperimeter of the triangle, and is given by:
| s = | a + b + c |
| 2 |
Substituting actual values to find s, we get:
| s = | 18 + 33 + 25 | = 38 |
| 2 |
Substituting actual values into heron's formula, we get:
area · √(38(38 - 18)(38 - 33)(38 - 25))
area · √(38(20)(5)(13)) · √49400 · 222.261
If we know the length of two sides of a triangle and the angle between them (i.e. the included angle), we can use the trigonometric sine function to find the area of the triangle. Consider triangle ABC below. We have dropped a perpendicular line from the apex of the triangle to its base. This line represents the height h of the triangle. It also divides triangle ABC into two right-angled triangles.
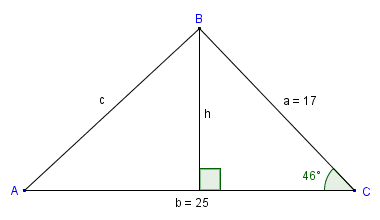
We can use the sine function to find the area if two sides and the included angle are known
Since we know the length of the base of the triangle (which in this case is side b), we could find the area of the triangle easily enough if we knew the height h. The sine function can help us out here. In a right-angled triangle, the sine of an acute angle gives the quotient of the side opposite the angle and the hypotenuse. In triangle ABC, we know the size of angle C and the length of side a, which is the hypotenuse of the right-angled triangle on the right of the diagram. From these facts we can derive the formula:
| sin (C ) = | h |
| a |
We can rearrange the equation to get h on the left-hand side:
h · a · sin (C )
Remember that the standard formula for the area of a triangle is:
| area · | base × height |
| 2 |
In our triangle, the base is side b, and the height is the line segment labelled h, so we can write:
| area = | bh |
| 2 |
However, since h is equal to a · sin (C ), we get:
| area = | ab · sin (C) |
| 2 |
Substituting actual values, we get:
| area = | (17)(25) · sin (46) |
| 2 |
| area = | 425 × 0.719 | = 152.79 |
| 2 |
We can also use the sine function to find the area of a triangle if we know the length of one side of the triangle and the size of two of its internal angles. More precisely, we make use of an equation known as the law of sines. Consider triangle ABC below.
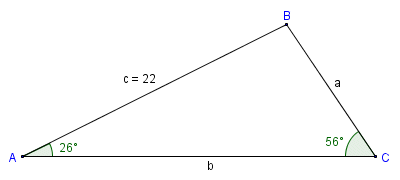
We can use the law of sines to find the area if two angles and one side are known
The law of sines, or sine rule, is an equation that expresses the relationship between the lengths of the sides of a triangle and the sines of its angles, for any triangle. It essentially states that the ratio of the length of one side of the triangle to the sine of the angle opposite that side will be the same for all three sides:
| a | = | b | = | c |
| sin (A) | sin (B) | sin (C) |
We can use this equation to find an expression for any side of the triangle, for example:
| a = | b · sin (A) |
| sin (B) |
or:
| a = | c · sin (A) |
| sin (C) |
Remember that we can find the area of a triangle using the sine function as follows:
| area = | ab · sin (C) |
| 2 |
In triangle ABC, we know the length of side b and the size of angles A and C. Angle A is adjacent to side c which we know the length of, so let's start by adjusting our area formula to take advantage of that:
| area = | bc · sin (A) |
| 2 |
The only term for which we don't have a value is b. However, we can use the law of sines to obtain an expression for b as follows:
| b = | c · sin (B) |
| sin (C) |
Now we can substitute for b in our area formula:
| area = | c2 · sin (B) · sin (A) |
| 2 · sin (C) |
Obviously, in order to use this formula we first need to find the value of angle B, but this is a relatively trivial matter since the sum of the internal angles of any triangle is always one hundred and eighty degrees, and we already know the values of angle A and angle C:
B = 180° - (A + C) = 180° - (26° + 56°) = 98°
Now we can substitute actual values into the formula:
| area = | 484 · sin (98) · sin (26) |
| 2 · sin (56) |
| area = | 484 x 0.990 x 0.438 | = 126.581 |
| 1.658 |
The formula requires us to know the value of all three of the triangle's internal angles, but providing we are given at least two of the angles, finding the value of the third angle is a trivial matter. Here is the general form of the area formula using the law of sines:
| area = | c2 · sin (A) · sin (B) |
| 2 · sin (C) |
Using the trigonometric functions to calculate the area of a triangle is relatively straightforward. The only thing you need to look out for is that the sides and angles may be labelled using a different naming convention to the one we have used here, so care must be taken to slot each value into the correct place in the formulas.
As we saw above, a right-angled triangle has one angle which is a right-angle (the name is a bit of a giveaway!). The two sides forming the right-angle are (by definition) perpendicular to one another, and the side opposite the right-angle is always the longest side. As we also saw above, a right-angled triangle may be either scalene (i.e. it has no two sides of equal length) or isosceles (the two sides forming the right-angle are of equal length). Given the presence of a right-angle in the triangle, and the fact that the internal angles of a triangle must always sum to one hundred and eighty degrees (180°), the second and third angles are always complementary (i.e. they always sum to ninety degrees (90°). In the case of an isosceles right-angled triangle, the other two angles are always forty-five degrees (45°). The right-angle in a right-angled triangle is usually denoted by a small square at the junction of the two sides forming the right-angle. These sides are known as the legs of the right-angled triangle. The longest side (i.e. the side opposite the right-angle) is called the hypotenuse.
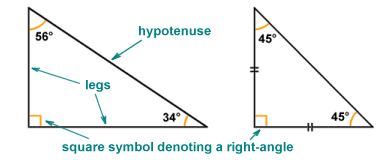
The anatomy of a right-angled triangle
The Greek philosopher and mathematician Pythagoras (who is believed to have lived during the sixth century BCE) is generally credited with the theorem that bears his name, although the principles it encompasses had been known about by Indian, Chinese, Babylonian and other Greek mathematicians for centuries. The theorem basically states that if you square the length of each leg of a right-angled triangle and add the values obtained together, the result is the same as you get by squaring the length of the side opposite the right-angle (the hypotenuse). The principle is illustrated in the following diagram:
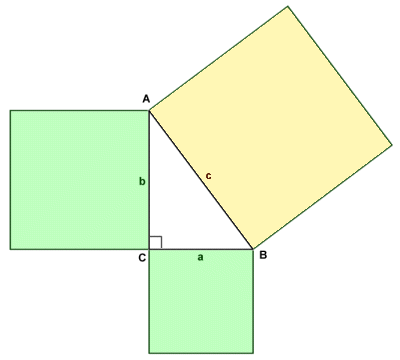
Pythagoras' theorem states that a2 + b2 = c2
The triangle ABC (illustrated above) is a right-angled triangle in which sides a and b are the legs of the triangle and side c is the hypotenuse. The relationship between the three sides is described by Pythagoras theorem and can be expressed algebraically as:
a2 + b2 = c2
If the lengths of two of the sides of a right-angled triangle are known, Pythagoras' theorem can be used to find the length of the third side. There are also several special kinds of right-angled triangle that have particular properties that are of interest to us. One such triangle is called a 3, 4, 5 triangle because one of its legs is three units in length, the other leg is four units in length, and the hypotenuse is five units in length. The reason this triangle is of interest is that the lengths can all be expressed as integer values. The units in question can be any arbitrary unit of measurement or some multiple thereof, and it can be shown that any triangle with sides in these proportions will always be a scalene right-angled triangle. The diagram below shows a 3, 4, 5 triangle.
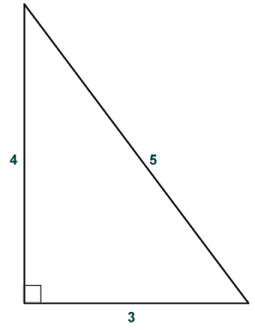
A 3, 4, 5 triangle
If we call the horizontal leg (or base) of the triangle a, the vertical leg b, and the hypotenuse c, we can apply Pythagoras' theorem to check that the 3, 4, 5 triangle is truly a right-angled triangle. If it really is a right-angled triangle, then a2 + b2 will be equal to c2:
a2 + b2 = c2 ⇒ 9 + 16 = 25
Since nine plus sixteen does equal twenty-five, the 3, 4, 5 triangle is indeed a right-angled triangle. The ratio 3:4:5 is called a Pythagorean triple. Several such ratios exist that involve only whole numbers. Another Pythagorean triple results in the ratio 5:12:13, which produces a right-angled triangle like the one shown below. The calculation (which appears below the diagram) confirms that these dimensions produce a right-angled triangle.
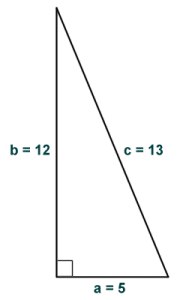
A 5, 12, 13 triangle
Here is the calculation:
a2 + b2 = c2 ⇒ 25 + 144 = 169
The isosceles right-angled triangle also has special properties. In addition to a right-angle it has two forty-five degree (45°) interior angles, and is sometimes referred to as a 45-45-90 triangle. The legs of the triangle (i.e. the sides that form the right-angle) are equal in length. The length of the hypotenuse of a 45-45-90 triangle is equal to the length of either one of the legs of the triangle (which we have labelled x in the diagram below) multiplied by the square root of two (hypotenuse = x√2).
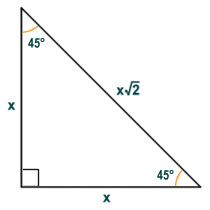
A 45-45-90 triangle
Another right-angled triangle with special properties is a scalene right-angled triangle which, in addition to a right-angle, has one thirty degree (30°) and one sixty degree (60°) interior angle. This type of triangle is commonly referred to as a 30-60-90 triangle for obvious reasons. The legs of the right-angled triangle are of course of different length, but interestingly the hypotenuse is exactly double that of the shorter leg (the leg opposite the thirty-degree angle), which we have labelled x in the diagram below (hypotenuse = 2x). The length of the longer leg (the leg opposite the sixty-degree angle), is meanwhile equal to the length of the shorter leg multiplied by the square root of three (longest leg = x√3).
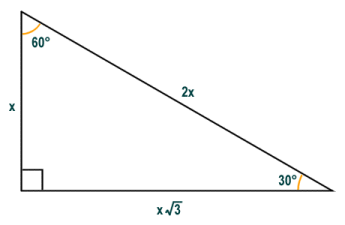
A 30-60-90 triangle
Two triangles are considered to be similar if every angle in one triangle is the same as the corresponding angle in the other triangle. The triangles may be different sizes (i.e. corresponding sides may have different lengths) but corresponding sides in the two triangles will differ from each other by the same ratio (this property alone is sufficient to establish a similarity between the two triangles).
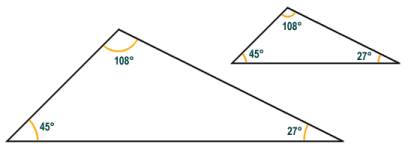
The triangles illustrated above are similar
Similarity between two triangles can be established if it can be shown that one of the following statements is true:
It can also be shown that if a line is drawn through a triangle such that it is parallel to one of the sides, and intersects the other two sides, it will divide them in the same proportion. The line effectively creates a new, smaller triangle within the original triangle that is similar to the original triangle. In the example illustrated below, triangle XBY is similar to triangle ABC.
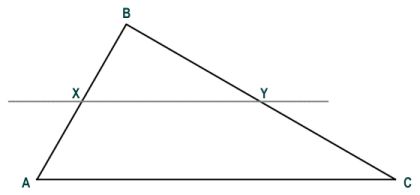
Triangle XBY is similar to triangle ABC
Two triangles are considered to be congruent if they have the same shape and are the same size. In order for this to be true, corresponding angles must be equal, and corresponding sides must be of the same length. The triangles illustrated below look very different at first glance, but closer examination will reveal that the corresponding angles and sides are in fact identical. The triangle on the right is an exact copy of the triangle on the left, but it has been rotated through an angle of one hundred and forty degrees (140°) clockwise.
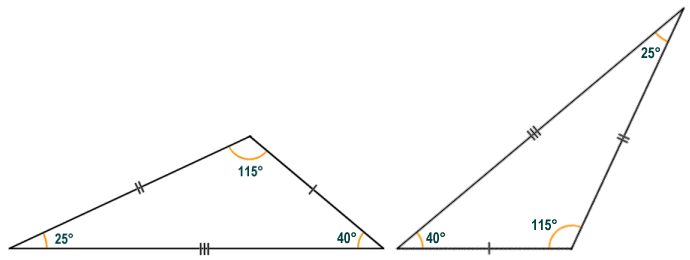
The triangles illustrated above are congruent
It can be established that two triangles are congruent if it can be shown that one of the following statements is true:
Various constructions involving triangles can be used to create important geometric points, lines and circles. We will describe some of the more significant of these constructions here. First of all, we will consider the construction involving a line that passes through each vertex of the triangle and is perpendicular to the side opposite that vertex. The construction is shown below. The point O at which these lines intersect is called the orthocentre of the triangle. In an acute triangle (a triangle in which all the angles are less than ninety degrees) like the one shown here, the orthocentre is inside the triangle. In an obtuse triangle (a triangle that contains an angle greater than ninety degrees) the orthocentre will be outside the triangle. In a right-angled triangle, the orthocentre will be at the vertex of the right-angle itself.
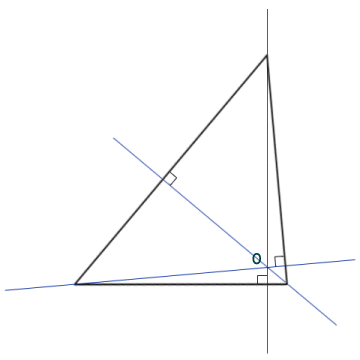
The position of the orthocentre depends on the type of triangle
The second construction we will look at involves a point called the centroid, which is created by the intersection of the medians of a triangle. A median is a line that passes through the vertex of a triangle and intersects the mid-point of the side opposite the vertex. It divides the triangle into two equal areas. The point O at which the centroid lies on each median is exactly twice as far from the vertex through which it passes as it is from the side of the triangle that it intersects. Interestingly, if the triangle were to be fabricated from a flat sheet of some suitable material of uniform thickness and density, the centroid would be the centre of mass for this triangular object.
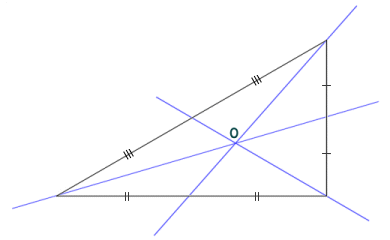
The centroid is the intersection of the medians
In the diagram below, each side of the triangle is intersected at its midpoint by a line that is perpendicular to (i.e. forming a right-angle with) the side. These lines are called perpendicular bisectors. The point O at which the perpendicular bisectors meet is called the circumcentre, because it is at the centre of a circle (the circumcircle) that passes through all three vertices of the triangle. The diameter and radius of the circle are called the circumdiameter and the circumradius respectively. If the circumcentre is inside the triangle, the triangle is an acute triangle (i.e. all of the angles are less then ninety degrees). If the circumcentre is outside the triangle, then the triangle is obtuse (i.e. one of the angles is greater than ninety degrees. If the circumcentre lies on one of the sides, then the triangle is a right-angled triangle (the right-angle will be the one opposite the side on which the circumcentre lies).
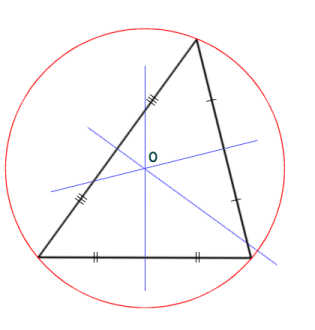
The circumcentre is the centre of a circle that passes through each vertex
The last construction we are going to look at here involves the lines that pass through the vertex of, and bisect, each of the triangle's internal angles (there are a number of other constructions involving triangles, but we will not be covering them here). The point at which these bisectors intersect one another is called the incentre, and lies at the centre of the triangle's incircle. The incircle is a circle that lies completely within the triangle, but touches all three sides. The radius of the incircle is called the inradius. Note that the centre of the incircle and the circumcircle do not coincide unless the triangle is equilateral (i.e. all three sides and all three internal angles are the same). Nevertheless, the existence of these two circles for all triangles means that all triangles can be said to be bicentric.
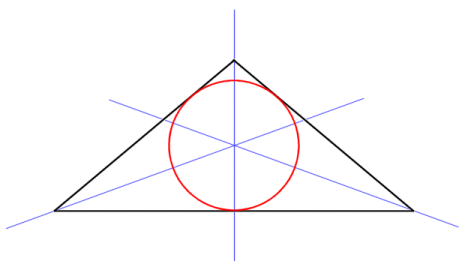
The incentre is the centre of a circle that touches all three sides