| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
A platonic solid is a regular convex polyhedron. The term polyhedron means that it is a three-dimensional shape that has flat faces and straight edges. The term convex means that none of its internal angles is greater than one hundred and eighty degrees (180°). The term regular means that all of its faces are congruent regular polygons, i.e. the sides of all faces are of the same length, and the internal angles of all faces are of equal magnitude. Furthermore, in order to qualify as one of the platonic solids, the shape must have the same number of faces meeting at each vertex, and the dihedral angle between any two faces must be the same. There are only five platonic solids in total:
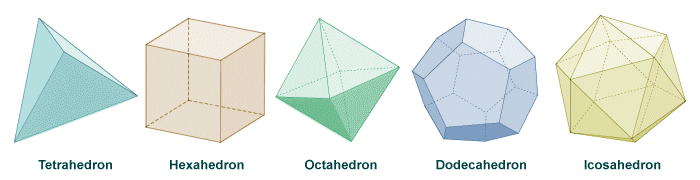
The five platonic solids
The names of the platonic solids reflect the number of faces that each one possesses. The term platonic is derived from the name of the Greek philosopher Plato, who is believed to have lived from around 423 to 347 BCE. Plato is known to have written about the shapes we know today as the platonic solids, although not in a particularly mathematical context. He is believed to have associated four of them (the tetrahedron, cube, octahedron and icosahedron) with the four classical elements (fire, earth, air, and water). In Plato's writings, the dodecahedron appears to be related to the arrangement of the constellations - perhaps a reference to the signs of the zodiac, although his exact meaning is not completely understood. One of Plato's contemporaries, the classical Greek mathematician Theaetetus, is credited with having formulated a mathematical description of all five platonic solids. Greek mathematician Euclid is believed to have drawn on the work of Theaetetus when writing the complete mathematical description of the platonic solids which appears in his later work, the Elements.
The main characteristics of the platonic solids are summarised in the table below. Note that, since the names used for the platonic solids are based on the number of faces each one has, these same names may be used to describe other three-dimensional solids that have the same number of faces.
| Name | Faces | Edges | Vertices | Dihedral angle | Vertex angle(s) | Shape of face |
|---|---|---|---|---|---|---|
| Tetrahedron | 4 | 6 | 4 | 70.53° | 60° | Equilateral triangle |
| Hexahedron | 6 | 12 | 8 | 90° | 90° | Square |
| Octahedron | 8 | 12 | 6 | 109.47° | 60°, 90° | Equilateral triangle |
| Dodecahedron | 12 | 30 | 20 | 116.57° | 108° | Regular pentagon |
| Icosahedron | 20 | 30 | 12 | 138.19° | 60°, 108° | Equilateral triangle |
As well as the features described above, the regularity of the platonic solids means that they are all highly symmetrical. For each platonic solid, it is possible to construct a circumscribed sphere or circumsphere (i.e. a sphere that completely encloses the platonic solid, and for which all of the vertices of the platonic solid lie on the surface of the sphere), a midsphere (i.e. a sphere that is tangent to each of the edges of the platonic solid), and an inscribed sphere or insphere (i.e. a sphere that is completely enclosed by the platonic solid, and that is tangent to each of its faces). For each of the platonic solids, these three spheres are concentric (i.e. they share a common centre). The radii of the spheres are called the circumradius, the midradius, and the inradius respectively.
The regular and symmetrical nature of a platonic solid also means that it is relatively straightforward to find its surface area or volume. This section contains separate pages that explore the characteristics of the regular hexahedron (or cube) and the tetrahedron (including the regular tetrahedron), including details of how to calculate the surface area and volume for these shapes. A more detailed description of the three remaining platonic solids, together with formulae for finding their volumes, their surface areas, and the radii of the various spheres associated with them is provided below.
A regular octahedron consists of eight equilateral triangles, with four of those triangles meeting at each vertex. It is in fact the only one of the platonic solids to have an even number of faces meeting at a single vertex. Various minerals have been found in the form of octahedral crystals, including diamond, alum and fluorite. There are also a number of games that use octahedral dice. In fact, dice have been produced in the shape of all of the platonic solids at one time or another, including octahedral poker dice. Interestingly, there are two different vertex angles (a vertex angle is the angles between two edges meeting at a vertex). At any vertex, the angle between adjacent edges is sixty degrees (60°), whereas the angle between opposite edges is ninety degrees (90°).
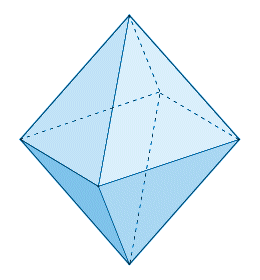
The octahedron has eight triangular faces
For an octahedron with an edge length of a, the formulae for finding the volume and surface area of the octahedron, together with those for finding the radii of its circumsphere, midsphere and insphere are given below.
| Volume = | √2a 3 |
| 3 |
Surface area = 2√3a 2
| Circumradius (radius of circumsphere) = | √2a |
| 2 |
| Midradius (radius of midsphere) = | a |
| 2 |
| Inradius (radius of insphere) = | √6a |
| 6 |
A regular dodecahedron consists of twelve regular pentagons, with three of those pentagons meeting at each vertex. There are a number of games in existence that use (twelve sided) dodecahedral dice, and some quasicrystals have a dodecahedral shape. A quasicrystal is usually a man-made crystalline structure, although naturally occurring examples have been discovered. Somewhat more intriguingly, in 2003 French and US cosmologists suggested, based on their interpretation of background microwave radiation patterns, that the universe is finite in size, and shaped like a dodecahedron.
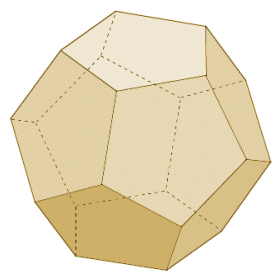
The dodecahedron has twelve pentagonal faces
For a dodecahedron with an edge length of a, the formulae for finding the volume and surface area of the dodecahedron, together with those for finding the radii of its circumsphere, midsphere and insphere are given below.
| Volume = | (15 + 7√5) a 3 |
| 4 |
Surface area = 3√ (25 + 10√5a 2)
| Circumradius (radius of circumsphere) = | (1 + √5) √3a |
| 4 |
| Midradius (radius of midsphere) = | (3 + √5) a |
| 4 |
| Inradius (radius of insphere) = |
|
||||||||||
| 2 |
A regular icosahedron consists of twenty equilateral triangles, with five of those triangles meeting at each vertex. There are a number of games in existence that use (twenty sided) icosahedral dice, probably the best known being the role playing game Dungeons and Dragons, first introduced in 1974 and still going strong (the game is currently in its fourth edition, and there have also been a number of minor revisions). The game uses, or has used in its various incarnations, dice shaped like all of the platonic solids, as well as a ten-sided version. In the natural world, the icosahedron is the shape favoured by a number of viruses, including the infamous herpes virus. The icosahedron is the only one of the platonic solids to have a dihedral angle with a magnitude greater than one hundred and twenty degrees. Like the octahedron, the icosahedron has two different vertex angles. At any vertex, the angle between adjacent edges is sixty degrees (60°), whereas the angle between non-adjacent edges is one hundred and eight degrees (108°).
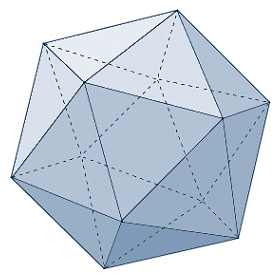
The icosahedron has twenty triangular faces
For an icosahedron with an edge length of a, the formulae for finding the volume and surface area of the icosahedron, together with those for finding the radii of its circumsphere, midsphere and insphere are given below.
| Volume = | 5 (3 + √5) a 3 |
| 12 |
Surface area = 5√3a 2
| Circumradius (radius of circumsphere) = | √ (10 + 2√5) a |
| 4 |
| Midradius (radius of midsphere) = | (1 + √5) a |
| 4 |
| Inradius (radius of insphere) = | √3 (3 + √5) a |
| 12 |