| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
A prism is a polyhedron (i.e. a three-dimensional geometrical shape with flat faces and straight edges) that has the same cross-sectional shape throughout its length, and is bounded at each end by two congruent and parallel polygons (sometimes referred to as the base faces). The remaining faces of the prism (i.e. the sides of the prism) are all parallelograms. The triangular prism (illustrated below) has perhaps one of the most recognisable shapes for a prism, but the cross section can be any polygonal shape. If we let the number of sides for one of the base face polygons equal n, then the prism will have n + 2 faces, 3n edges, and 2n vertices. Any cross section taken through the prism parallel to the base faces is identical to the base faces.
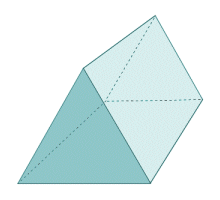
A triangular prism
Apart from the fact that they can have differently-shaped cross sections, prisms can also be categorised as right prisms or oblique prisms. A right prism is one for which the sides of the prism are perpendicular (i.e. at right angles) to the base faces. This requires all of the side faces of the prism to be rectangular in shape. An oblique prism is one for which the sides of the prism are not perpendicular to the base faces. In this case, all of the side faces of the prism will be non-rectangular parallelograms. Note that if the base faces are regular polygons and the side faces are square, the prism may be referred to as a uniform prism. Prisms of this type are a subset of the set of uniform polyhedra. A uniform polyhedron is one for which all of the faces are regular polygons (i.e. polygons for which all of the sides are of equal length).
From the above definitions it follows that both a cube and a cuboid are right prisms, and a cube is also a uniform prism (since all of its faces are square) as well as being both a uniform polyhedron and a regular polyhedron. A parallelepiped also fits the definition of a prism since each pair of opposite faces consists of parallel and congruent parallelograms (it is worth noting that cubes and cuboids can also be considered to be parallelepipeds).
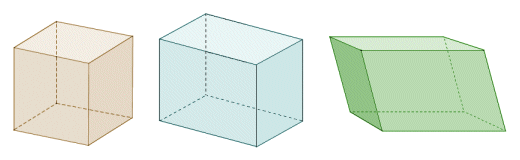
Cubes, cuboids and parallelepipeds are all examples of prisms
Another term you may come across is regular prism. This means that the base faces of the prism are regular polygons. Since the base faces of a prism must be congruent and parallel, all of the side faces of a regular prism will therefore have the same dimensions. An irregular prism is one for which the base faces are not regular polygons. It follows that the side faces of an irregular prism will not all have the same dimensions.
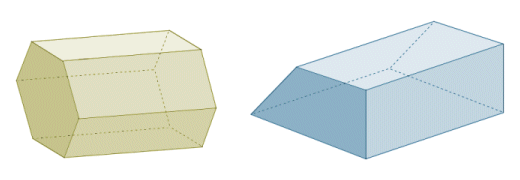
A regular hexagonal prism (left) and an irregular prism (right)
An interesting question arises over whether it is possible to have a cylindrical prism. If the base faces of a cylinder are both congruent and parallel, the cross section will certainly conform to the requirements of a prism. The sticking point is over the requirement that the base faces of a prism must be polygons. Since the base face of a cylinder must be either a circle or an ellipse, it is often argued that the cylinder cannot be a prism because neither a circle nor an ellipse is a polygon. On the other hand, it can also be argued that, since there is theoretically no limit to the number of sides that a polygon may have, a circle (or an ellipse) is simply a polygon with an infinite number of sides.
As always, we are often required to find the volume and surface area of a prism. For a right prism, finding the volume is relatively straightforward. All we need to do is multiply the area A of one of the base faces of the prism by the length of the prism. It is useful here to think of the prism as standing on one of its base faces. The length of the prism then becomes its height, h. We can therefore write the formula for finding the volume V of a prism as:
V = Ah
This also works for an oblique prism, if we consider the height to be the perpendicular distance between the two base faces. If we stand any prism on one of its base faces, whether the prism is a right prism or an oblique prism, then its height (sometimes referred to as its altitude) will indeed be the perpendicular distance between the two base faces. The illustration below demonstrates the principle.
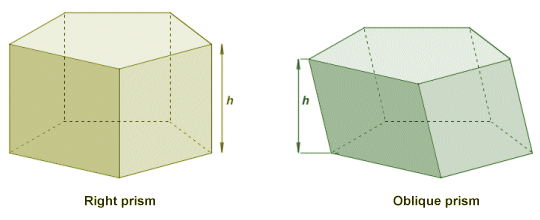
The height of a prism is the perpendicular distance between its base faces
Finding the surface area of a prism is also relatively straightforward. The total surface area A will be the area of the base B multiplied by two, plus the lateral area of the prism (the lateral area is the sum of the areas of the sides of the prism). The lateral area is found by multiplying the perimeter p of the prism by its height h. We can therefore write the formula for finding the total surface area of a prism as:
A = 2B + ph