| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Cubes, cuboids and parallelepipeds are closely related three-dimensional polyhedra (a polyhedron is any three-dimensional shape that has straight edges and flat faces). You can probably think of the parallelepipeds as a family of shapes to which cuboids belong. Not all parallelepipeds are cuboids, but all cuboids are parallelepipeds. Similarly, cubes are a subset of the cuboid family and, although all cubes are cuboids (and hence also parallelepipeds), not all cuboids are cubes. Cubes and parallelepipeds are discussed elsewhere. This page is concerned with cuboids. Cuboids (including of course cubes) are found frequently in everyday life. Most rooms in homes, offices, and other types of building are basically cuboids. Building materials such as bricks, blocks and wooden beams are cuboids. Packing cases, boxes and cartons (for example, food containers) are more often than not cuboids.
As stated above, a cuboid is a three dimensional shape with straight edges and flat faces, or polyhedron. It is not a regular polyhedron unless it is also a cube, but it is sometimes called a rectangular polyhedron because all of the faces are rectangles. A cuboid has six (6) faces. Opposite faces are congruent, but adjacent faces will often be of different lengths. Likewise, a cuboid has twelve (12) edges that can have different lengths (although opposite edges of the same face will always be of the same length). The dihedral angle between all intersecting faces is ninety degrees (90°). Each of the cuboid's eight (8) vertices is formed by the junction of three of its faces. The cuboid can also be called a hexahedron (a hexahedron is any three-dimensional shape with six faces).
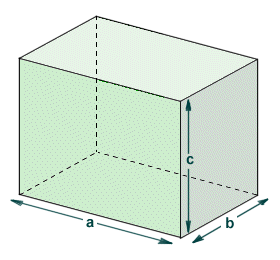
The cuboid is a rectangular polyhedron
The name "cuboid" is indicative of the shape of this rectangular polyhedron, i.e. it is similar in shape to a cube. Indeed, a cuboid for which the dimensions a, b and c are equal is a cube, and the faces are congruent squares. When we refer to a shape as a cuboid, we usually mean a shape that is similar to a cube, but not actually a cube. Probably the most famous reference to a cuboid in popular culture is the monolith first described in Arthur C. Clarke's short story "The Sentinel" and later immortalised in Stanley Kubrick"s 1968 film "2001: A Space Odyssey". According to the story, the monolith in question was created by a race of intelligent aliens, and causes an evolutionary leap in a pre-human species of ape. The dimensions of the monolith are in the ratio one:four:nine (1 : 4 : 9). The significance of these numbers is that they are the squares of one, two and three (1, 2 and 3) respectively.
The ratios of the various edges and diagonals of a cuboid is of special interest to mathematicians. A cuboid that has both integer edges and integer face diagonals is called an Euler brick (named after the eighteenth century Swiss mathematician Leonhard Euler). An Euler brick that also has an integer space diagonal would be a perfect cuboid. I say "would be", because to the best of my knowledge, no one has so far determined whether a perfect cuboid actually exists. Anyway, getting back to slightly more mundane issues, the most important formulae relating to the characteristics of a cuboid for which the dimensions are a, b and c are given in the following table:
| Characteristic | Formula |
|---|---|
| Surface area: | = 2ab + 2ac + 2bc |
| Volume: | = abc |
| Face diagonal (a, b): | = √(a2 + b2) |
| Face diagonal (a, c): | = √(a2 + c2) |
| Face diagonal (b, c): | = √(b2 + c2) |
| Space diagonal: | = √(a2 + b2 + c2) |
The first two formulae require little explanation. The surface area of a cuboid is simply the sum of the surface areas of its six faces. There will be three pairs of faces, one pair having dimensions a multiplied by b, one pair with dimensions a multiplied by c, and one pair with dimensions b multiplied by c. The total surface area will thus be the sum of the products of dimensions a and b, a and c, and b and c multiplied by two. The volume of the cuboid is simply the product of dimensions a, b and c. The face diagonal (of which there will be two for each face) is the line segment connecting opposite corners of any face of the cuboid, as shown below. It forms the hypotenuse of a right-angled triangle in which each leg is formed by one edge of the cube. Its length will depend on which face it belongs to, since each pair of opposite faces may have a different set of dimensions.
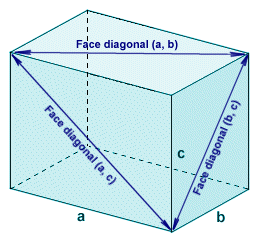
The face diagonals connects opposite corners of each face
The space diagonal is the line segment connecting opposite corners of opposite faces of the cuboid, as shown below. It forms the hypotenuse of a right-angled triangle in which one leg is one of the face diagonals and the other leg is one of the edges of the cube. Unlike the face diagonals, all of the space diagonals (of which there will be four) are equal in length. Each face diagonal can be the hypotenuse for three differently dimensioned right-angled triangles, depending on which edge is chosen as one of the legs.
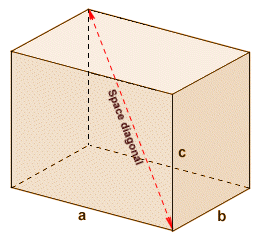
The space diagonal connects opposite corners of opposite faces