| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The use of the term sphere in this page refers to the three-dimensional solid, every point on the surface of which is equidistant from its centre. Many mathematicians would argue that such an object should in fact be called a ball, and that the term sphere is more correctly used to describe only the set of points that are equidistant from some given central point in a three-dimensional space. Paradoxically, this would make the sphere a two-dimensional object existing in a three-dimensional space (since the surface alone consists only of a collection of points and thus has no thickness). Such an argument is certainly valid in the realms of higher mathematics. However, the term sphere is consistently used (or perhaps misused) in everyday language to refer to both spherical (i.e. ball-shaped) solids and hollow spheres. We will therefore not differentiate on this page between the terms sphere and ball.

A football is (approximately) spherical in shape
The distance from the centre of a sphere to any point on its surface is called the radius. In fact, the length of the radius is the only piece of information we actually need in order to calculate the volume and surface area of the sphere. The maximum distance that can exist between any two points on the surface of a sphere is a diameter of the sphere. A line segment drawn between two such points will always pass through the centre of the sphere, and will be twice the length of the radius. Any two points that lie at opposite ends of a diameter of a sphere are called antipodal points (people in Great Britain used to refer to Australia and New Zealand as "the Antipodes" due to the fact that these countries were on the opposite side of the globe).
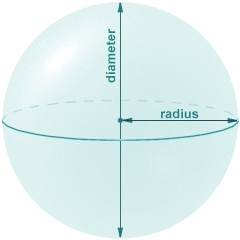
The diameter and radius of a sphere
Any circle on the sphere that passes through two antipodal points must, by definition, have the same radius and diameter as the sphere, and will partition the surface of the sphere into two equal hemispheres. Such a circle is sometimes called a great circle. You can think of the Earth's equator as a great circle, since it partitions the Earth into two hemispheres (the northern hemisphere and the southern hemisphere), although the Earth itself is not strictly speaking a sphere. The shortest arc that can be drawn on the surface of a sphere between any two non-antipodal points will lie on the unique great circle that passes through both of those points. The arc is a segment of the great circle, and is also a geodesic (the term geodesic means the shortest possible distance between two points on a curved surface).
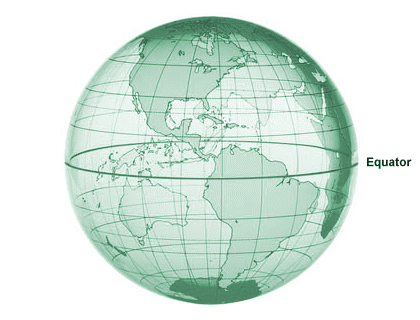
The equator is a great circle that separates the globe into two hemispheres
The sphere is perfectly symmetrical, and has the smallest ratio of surface area to volume of any three-dimensional shape. In other words, for any given volume, the smallest surface area able to completely enclose that volume is a sphere. For this reason the sphere is frequently encountered in the natural world. Water droplets and gas bubbles, for example, belong to a class of objects that scientists call minimal surface structures. The internal and external forces at work within and around these structures force them to assume the shape that has the smallest possible surface area for the volume contained, which is a sphere.
It is generally believed that the formulae for finding the volume and surface area of a sphere were first discovered by the Greek mathematician and philosopher Archimedes in the third century BCE. Archimedes was able to demonstrate that the surface area of a sphere is exactly the same as the lateral surface area of a right circular cylinder for which both the diameter and altitude are equal to the diameter of the sphere. Such a cylinder could completely contain the sphere, with its base faces tangent to the surface of the sphere at antipodal points (if you need an explanation of any of the italicised terms, see the page entitled "Cylinders"). We would call this cylinder the sphere's circumscribed cylinder (conversely, the sphere is the cylinder's inscribed sphere).

A sphere with its circumscribed cylinder
The lateral surface area LSA of the circumscribed cylinder is given by:
LSA = 2πrh
where r is the radius of the cylinder and h is the height (or altitude) of the cylinder. Since the radius of the cylinder is equal to that of the sphere, and since the height of the cylinder is equal to the diameter of the sphere (i.e. twice the radius), we can rewrite the formula as:
LSA = 2πr (2r) = 4πr 2
Since we know that the surface area A of a sphere is the same as the lateral surface area of its circumscribed cylinder, then we also have the formula for the surface area of a sphere:
A = 4πr 2
Archimedes was also able to demonstrate that the volume of a sphere is two-thirds that of its circumscribed cylinder. First, therefore, let's consider the volume Vcyl of the cylinder. This is given as the area of one of the cylinder's base faces multiplied by its height. In terms of the inscribed sphere's radius, therefore, we can write the formula as:
Vcyl = πr2 (2r) = 2πr 3
Since we know that the volume V of a sphere is equal to two thirds of the volume of its circumscribed cylinder, we can now use this knowledge to derive the formula for the volume of a sphere as follows:
| V = | 2 | 2πr 3 = | 4 | πr 3 |
| 3 | 3 |